Теория автоматического управления. Нелинейные системы

4. УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ

4.1.Понятие устойчивости нелинейных систем

Применение методов исследования линейных систем для анализа динамики нелинейных систем возможно с учетом двух понятий движения:

1)невозмущенное движение – одно из возможных расчетных движений системы при определенных начальных условиях и заданном внешнем воздействии;

2)любое другое движение – возмущенное, получаемое за счет приложения к системе кратковременного внешнего возмущения при t = 0.

Процессы в автономных нелинейных системах можно рассматривать как частные случаи невозмущенных движений, при исследовании которых важным вопросом является анализ стационарных (установившихся) движений. При анализе их устойчивости рассматриваются два вида устойчивости движения: устойчивость со-

стояния равновесия и устойчивость периодических движений (автоколебаний).

Пусть нелинейная система управления описывается системой обыкновенных дифференциальных уравнений с постоянными коэффициентами в векторной форме

где x – вектор состояния x = x(x1, x2,…xn), φ – вектор-функция,

φ = φ(φ1, φ2, … φn).

Функции φk и их производные по всем переменным хj в (4.1)

непрерывны.

Решение системы будет x(t), определяемое вектором начальных условий, заданных в некоторый момент времени t = t0 x0 = = x0(x10, x20, …xn0).

71

elib.pstu.ru

Обычно t0 = 0, поэтому более наглядным является решение: x1 = x1(t, x0), x2 = x2(t, x0),… xn = xn(t, x0) и в векторной форме x =

= x(t, x0).

Решение системы может быть получено линеаризацией непрерывных функций φk, тогда как во многих случаях в нелинейных системах функции φk являются кусочно-линейными, разрывными и даже неоднозначными.

4.1.1. Анализ стационарных движений

Состояние равновесия как вид стационарного движения описывается системой конечных уравнений, получаемых из системы (4.1), когда производные равны нулю:

0 = φ1(x1, x2, … xn), 0 = φ2(x1, x2, … xn),

………………….. (4.2)

0 = φn(x1, x2, … xn).

Пусть система (4.2) имеет m решений a(a1i, a2i,… ani) для i = 1,2…m, тогда для системы (4.1) имеем

Решения по (4.3) называются стационарными движениями, хотя им соответствует точка, пребывающая в неподвижном состоянии.

Вторым классом стационарных движений в динамической нелинейной системе являются периодические движения, в процессе которых переменные совершают колебания с периодом Т:

Различают два принципиально разных вида периодических движений: предельные циклы и консервативные движения.

Предельный цикл представляет собой изолированную замкнутую траекторию. В достаточно малой окрестности этой траектории не существует других замкнутых траекторий. Все траектории в этой окрестности или «наматываются» на предельный цикл, или удаляются от него.

72

elib.pstu.ru

Предельным циклам фазового пространства в системе соответствуют автоколебания. Присущие линейным системам консервативные движения в нелинейных системах встречаются редко.

Устойчивость положения равновесия определяется по Ляпу-

нову, следующим образом.

Пусть положение равновесия системы a(a1, a2,… an). Состояние равновесия a называется устойчивым, если для ка-

ждого заданного (сколь угодно малого) положительного числа ε можно найти такое положительное число δ(ε), при котором выполнение неравенства:

для всего бесконечного интервала времени 0 < t < ∞ будут справедливы неравенства

Положение равновесия называется асимптотически устойчивым по Ляпунову, если дополнительно к (4.4) и (4.5) имеет место условие

Если существует такое ε, при котором хотя бы в одном случае нельзя найти такое число δ(ε), чтобы было выполнено (4.5) для всех t > 0, то положение «a» называется неустойчивым по Ляпунову.

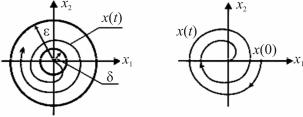
На рис. 4.1 проиллюстрированы понятия устойчивости по Ляпунову и частного случая асимптотической устойчивости.

Рис. 4.1. К понятию устойчивости по Ляпунову (траектория х(х0, t) начинается в некоторой δ-окрестности и не покидает ε-окрестность)

73

elib.pstu.ru

Пример 4.1

1.Пусть уравнение системы x′= –x, решение которого x(t) = x0 e–t. Точка равновесия х = 0 асимптотически устойчива, так как при любом значении х0 функция x(t)→0 при t→∞.

2.Решением уравнения x′= + x является x(t) = x0 et. Точка равновесия неустойчива, так как при любом значении х0 функция x(t)→∞ при t→∞.

3.Пусть x1' = − x2 и x2' = x1 . Этой системе соответствует уравне-

ние консервативного звена x2'' + x2 = 0 . Его решение x2(t) = A sin(t + ξ),

где А и ξ – постоянные интегрирования. Всегда по заданному ε можно выбрать δ таким образом, чтобы окружность имела радиус меньше ε. Положение равновесия х1 = 0, х2 = 0 устойчиво по Ляпунову, но не асимптотически устойчиво.

Устойчивость по Ляпунову для периодических движений

определяется относительно периодического решения φ(t) системы,

описываемой (4.1). Периодическое решение φ(t) называется ус-

тойчивым по Ляпунову, если для каждого заданного положительного числа ε можно найти такое положительное число δ(ε), при котором выполняется неравенство

топериодическое движение асимптотически устойчиво по Ляпунову. Ограничения, налагаемые условием устойчивости по Ляпунову, выполняются редко. Поэтому для периодических движений используется условие устойчивости, называемое орбитной устойчи-

востью.

Периодическое движение φ(t) называется орбитно-устойчи-

вым, если для любого ε можно найти такое δ(ε), при котором любая фазовая траектория, находящаяся при t = t0 в δ-окрестности траекто-

74

elib.pstu.ru

рии периодического движения, для всех t = t0 ÷ ∞ не выйдет из ε-окрестности траектории периодического движения.

Орбитная устойчивость требует близости не изображающих точек решения φ(t) и близкого к нему при t = t0 решения x(t), а близости траектории этих точек в пространстве.

Периодическое движение называется асимптотически орбитноустойчивым, если все упомянутые траектории при t→∞ асимптотически приближаются ктраектории периодического движения φ(t).

Пояснение окрестности к понятию орбитной устойчивости дано на рис. 4.2, где показана часть замкнутой траектории φ(t).

Рис. 4.2. К пояснению орбитной устойчивости

4.2. Методы определения устойчивости положения равновесия

В 1892 г. А.М. Ляпунов опубликовал классическую работу «Общая задача об устойчивости движения». В этой работе предложены два метода исследования устойчивости положения равновесия.

Первый метод: определение устойчивости положения равновесия по уравнению первого приближения. Это уравнение, следуя принятой в технике традиции, будем называть линеаризованным

уравнением.

Второй метод (прямой метод Ляпунова) сводится к построению некоторых функций, называемых функциями Ляпунова.

75

elib.pstu.ru

4.2.1 Линеаризация нелинейных систем, описываемых дифференциальными уравнениями n-го порядка

Если требуется провести линеаризацию уравнения движения

при некотором входном сигнале roп (t) и начальных условиях,

то поведение x(t) нелинейной системы в окрестности опорной траектории может быть представлено с помощью отклонений x(t) от

где вариация внешних воздействий δr(t) = r(t) − roп (t).

Разложим функцию F в ряд Тейлора в окрестности опорной траектории. Ограничившись только линейными членами уравнения и вычитая (4.12) из (4.13), получим, что вариации δ x(t) описываются системой линейных уравнений:

δx&(t) = Fx [t, xoп (t),roп (t)]δx(t) + Fr [t, xoп (t),roп (t)]δr(t) ,

где Fx и Fr – матрицы частных производных вектор-функции F(t, x, r) по соответствующим аргументам,

76

elib.pstu.ru

Дальнейший анализ нелинейной системы в окрестности опорного режима проводится методами анализа линейных систем, применяемыми к уравнениям в вариациях (4.14).

Пример 4.2

Пусть требуется провести линеаризацию системы, описываемой нелинейным дифференциальным уравнением функции одной переменной

F = x′′′ + (x′′)2 + sinx′ + eх –1 + r2 – r = 0

с начальными условиями x(0) = x0, x′(0) = x′0, x′′(0) = x′′0 относи-

тельно опорной траектории xоп(t) ≡ 0, rоп(t) ≡ 0.

Определим коэффициенты разложения функции F в ряд Тейлора:

a3 = (∂F/∂x′′′)оп = 1, a2 = (∂F/∂x′′)оп = (2x′′)оп = 0,

a1 = (∂F/∂x′)оп = (cosx′)оп = 1,

a0 = (∂F/∂x)оп = (eх)оп = 1, b1 = –(∂F/∂r′)оп =

= –(2r′)оп = 0, b0 = –(∂F/∂r)оп = 1.

Отсюда получим дифференциальное уравнение линеаризованной системы:

δx′′′(t) + δx′(t) + δx = δr(t);

λ2,3 = 0,3412 ± 1,1615i , из которых λ2,3 имеют положительную ве-

щественную часть, поэтому согласно теоремам первому методу Ляпунова система неустойчива.

77

elib.pstu.ru

4.2.2. Линеаризация нелинейных систем, описываемых дифференциальными уравнениями в форме Коши

Метод применяется для исследования устойчивости нелинейных систем по линеаризованным уравнениям для малых вариаций переменных.

Применим первый метод Ляпунова к дифференциальным уравнениям в пространстве состояний нелинейных систем.

Пусть динамическая система описывается уравнением

где x – вектор состояния, φ – вектор-функция.

Обозначим через x* вектор координат исследуемого положения равновесия, т.е. решение системы уравнений φ(x) = 0, и положим, что функция φ допускает разложение в ряд Тейлора в точке x*. Пренебрегая малыми высшего порядка по сравнению с малыми вариациями δx, получим уравнение линеаризованной системы

– матрица первых производных нелинейной функции (матрица Якоби), вычисляемых в точке равновесия x = x*.

Согласно первому методу Ляпунова об устойчивости «в малом» положения равновесия нелинейной системы можно судить по результатам анализа линеаризованной системы:

• если все собственные значения матрицы А имеют отрицательные действительные части, т.е. линеаризованная система устойчива асимптотически, то положение равновесия устойчивое;

78

elib.pstu.ru

•если линеаризованная система неустойчива, то положение равновесия неустойчивое.

•если среди собственных значений (характеристических чисел) матрицы системы имеется хотя бы два мнимых сопряженных значения, для суждения об устойчивости использовать линеаризо-

ванную систему нельзя. Необходимо при разложении функции в ряд использовать нелинейные члены.

Исследование устойчивости нелинейных систем по первому методу Ляпунова имеет недостатки:

•исследуется только устойчивость «в малом»;

•применим только для систем, линеаризуемых в окрестности

положения равновесия.

Применение данного метода рассмотрим на примере с помощью первого метода Ляпунова.

Пример 4.3

Пусть математическое описание системы в форме Коши имеет

вид:

dx1 = − x1 + x1x2 ; dt

dx2 = − x2 + x22 . dt

Определим положение равновесия нелинейной системы, приравняв нулю производные. Получаем, что система имеет два реше-

ния: x11 = 0; x21 = 0 и x12 = 0; x22 = 1 которые являются точками равновесия системы.

Для применения первого метода Ляпунова линеаризуем исходную нелинейную систему разложением в ряд Тейлора в окрестности точек состояния равновесия, в результате чего получим:

ϕ1 (x1, x2 ) ≈ a11∆x1 + a12∆x2 ;

ϕ2 (x1, x2 ) ≈ a21∆x1 + a22∆x2 .

На рис. 4.3 показано пояснение принципа перехода к линеаризованной системе уравнений, где для коэффициентов (переменных)

79

elib.pstu.ru

fji в системе уравнений индекс j – № функции (переменной), а i – № числа состояния равновесия.

Рис. 4.3. Линеаризация в окрестности положения равновесия

Проверку устойчивости выполним для каждого состояния равновесия:

1. Значения коэффициентов линеаризованного уравнения:

Тогда линеаризованная система уравнений для первого состояния равновесия примет вид:

dx1 = − x1; dt

80

elib.pstu.ru