
Теория автоматического управления. Нелинейные системы
.pdf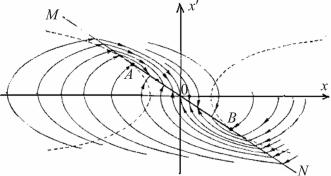
Рис. 2.16.Фазовый портрет возникновения скользящего режима
В точках А и В, как и на отрезке АВ, изображающая точка не сможет двигаться по новому листу из точек переключения, так как соответствующая фазовая траектория уходит за его границу. Это означает, что переход с одного листа на другой невозможен. В этом случае изображающая точка начнет двигаться по самой линии переключения (рис. 2.15, а), что физически будет соответствовать колебаниям с бесконечно малой амплитудой и бесконечно большой частотой (рис. 2.15, б).
Таким образом, введение в систему дополнительного воздействия по производной позволяет устранить установившиеся (рис. 2.13) или расходящиеся (рис. 2.14) периодические режимы. При этом имеется возможность получения качественно новых режимов в нелинейных системах.
2.5.3. Исследование релейной системы управления
объектом с W ( p) = |
|
|
k |
p |
( |
) |
|
|
|
Tp +1 |
Релейные системы управления объектом с передаточной функцией, рассмотренной в п. 2.5.2, встречающиеся в задачах автоматизации производственных процессов, являются инерционными.
Запишем систему дифференциальных уравнений свободного движения системы в форме Коши (х1 = ε):
41
elib.pstu.ru
|
|
|
|
|
|
|
|
dx1 |
|
= x2 |
= |
dε |
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
||||||||||||
|
|
|
|
|
|
|
T |
dx2 |
+ x2 |
= −ku . |
(2.22) |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда получим |
dx1 |
|
= x2 , |
|
|
|
|
|
|
|
|
|
|
|||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dx2 |
= −(x2 + ku) / T = −[x2 + kF(x1 )] / T . |
(2.23) |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поделим второе уравнение на первое: |
|
|||||||||||||||||||||||
|
|
|
|
dx2 |
|
= −[x2 + kF(x1 )] / Tx2 . |
(2.24) |
|||||||||||||||||
|
|
|
|
dx1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если учесть, что на различных интервалах x1 функция F(х1) по- |
||||||||||||||||||||||||
стоянна, разделив переменные в уравнении (2.24) |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
x2dx2 |
|
= − |
1 |
|
|
dx1 , |
|
||||||||||
|
|
|
|
|
x2 + kF(x1 ) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
T |
|
||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 − kF(x1 )ln |
|
x2 + kF(x1 ) |
|
= − |
x1 |
+ С , |
(2.25) |
||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
где С – постоянная, определяемая начальными условиями. Многолистная фазовая плоскость будет иметь уравнения фазо-
вых траекторий при различных значениях F(х1):
x1 < −а, |
x2 |
|
+ kC ln |
|
x2 |
− kC |
|
= − |
1 |
x1 + С ; |
(2.26) |
|||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
T |
|
|||
|
x1 |
|
≤ а , x2 = − |
x1 + С ; |
(2.27) |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
||||||||||
x1 > а, |
x2 |
|
− kСln |
|
x2 |
+ kC |
|
= − |
1 |
x1 + С . |
(2.28) |
|||||||||
|
|
|
||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
||||
42
elib.pstu.ru
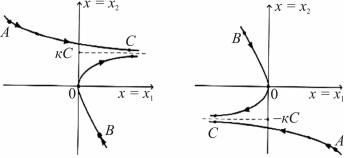
Рис. 2.17. Фазовые траектории системы при |х1| > a
На рис. 2.17 приведены фазовые траектории, описываемые уравнениями (2.26) и (2.28), где при |х2| > кС имеют вид АС, а при меньших начальных значениях скорости изменения выходной переменной системы – ВС. Для случая, описываемого уравнением (2.27), на листе фазовой плоскости вид траекторий соответствует рис. 2.4, а. При этом фазовый портрет системы обладает отрезком равновесия, равном нечувствительности реле.
Границами трёх «листов» фазовой плоскости являются линии переключения, описываемые х1 = ± а. Движение системы завершается на отрезке равновесия.
В качестве примера построения фазовых траекторий на рис. 2.18 приведен фазовый портрет системы со статической характеристикой двухпозиционного реле сгистерезисом.
На фазовом портрете системы имеется устойчивый предельный цикл (к замкнутому контуру стремятся все фазовые траектории независимо от начальных условий).
Применение воздействий по производной дает возможность улучшения динамических показателей качества системы, вплоть до получения скользящего режима. На рис. 2.19, а показано изменение параметров предельного цикла в системе при наличии гибкой обратной связи, что обеспечивает уменьшение амплитуды автоколебаний (амплитуда автоколебаний по предельному циклу MN меньше гистерезиса реле).
43
elib.pstu.ru
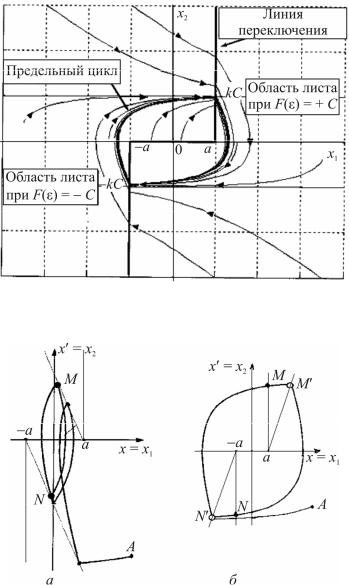
Рис. 2.18. Фазовый портрет системы с гистерезисной статической характеристикой реле
Рис. 2.19. Фазовые траектории:
а– при введении гибкой отрицательной обратной связи;
б– при наличии запаздывания в системе
44
elib.pstu.ru

Наличие в системе запаздывания приводит к тому, что сигнал реле будет переключаться с опозданием на время τ. В течение промежутка времени τ изображающая точка будет двигаться по старой траектории. Таким образом, запаздывание не изменит формы фазовых траекторий на листах, но поворачивает вправо линии переключения изображающей точки с одного листа на другой, что приводит к ухудшению динамических показателей, вплоть до возникновения автоколебаний.
На рис. 2.19, б показано изменение параметров предельного цикла при наличии в системе запаздывания. Угол поворота линий переключения α в положительном направлении определяется уравнением
tgα ≈ [(x1M) – (х1М’)]/x2M. |
(2.29) |
2.6. Построение фазовых траекторий
Построение фазовых траекторий можно выполнить по уравнению, полученному в результате решения системы нелинейных дифференциальных уравнений, представленных в форме Коши. В связи с встречающимися трудностями их решения разработаны другие методы, например:
–метод моделирования систем;
–метод изоклин;
–метод припасовывания;
–метод точечных преобразований.
Наиболее универсальным из последних является метод изоклин. Сущность метода заключается в построении таких линий, проходя через которые, все фазовые траектории имеют один и тот же угол наклона касательной. Пусть система описывается уравнением
(2.5) фазовых траекторий в дифференциальной форме
dx2 = f2 (x1, x2 ) . dx1 x2
Принимая наклон касательных к фазовой траектории χ = const, получим уравнение линии, в любой из точек которой фазовая тра-
45
elib.pstu.ru
ектория имеет один и тот же угол наклона. Тогда из предыдущего уравнения получим уравнение изоклины:
x2 = f2(x1, x2)/χ. |
(2.30) |
Порядок построения фазовой траектории показан на примере устойчивой линейной системы 2-го порядка в соответствии с (2.11)
на рис. 2.20.
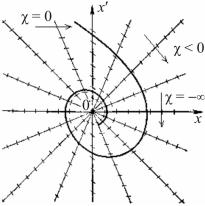
На фазовую плоскость наносят семейство изоклин для различных значений χ, после чего вдоль каждой изоклины вычерчивают ряд параллельных отрезков с углом наклона χ. На рис. 2.20 показаны изоклины в виде прямых, проходящих через начало координат, которые пересекаются фазовыми траекториями, касательные к которым имеют значения наклонов χ.
Фазовая траектория получается построением плавной кривой, пересекающей каждую изоклину под соответствующим углом.
Рис. 2.20. Построение фазовых траекторий методом изоклин
2.7. Построение кривой переходного процесса по фазовой траектории
Рассмотрим приближенное построение переходного процесса по фазовой траектории. Для построения процессов по интересующему отрезку фазовой траектории требуется определить время
46
elib.pstu.ru
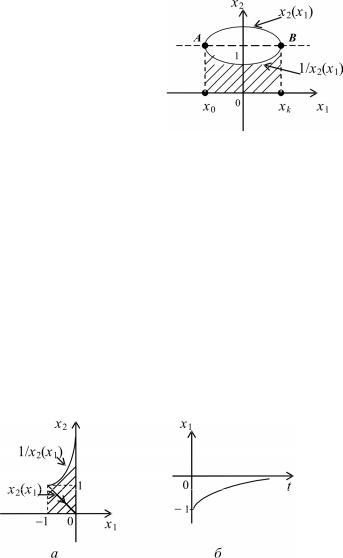
движения изображающей точки на отрезке фазовой траектории. Зафиксируем интересующий нас отрезок AB фазовой траектории x2(x1), как это показано на рис. 2.21.
Определим время ∆t , за которое изображающая точка пройдёт от начала отрезка AB х1 = х0 до его конца х1 = хк.
По определению имеем
|
dx1 |
= x2 |
, тогда |
dx1 |
= dt . |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
||
|
|
Интегрируя это выражение, |
|
Рис. 2.21. Отрезок AB |
|
||||||||
получим |
|
|
|
|
|
|
фазовой траектории x2(x1) |
|
|||||
|
|
|
|
|
xk |
dx |
|
t |
|
|
|
|
|
|
|
|
|
|
∫ |
= t |
k |
= tk |
− t0 = ∆t. |
|
|||
|
|
|
|
|
|
1 |
|
(2.31) |
|||||
|
|
|
|
|
x |
(x ) |
t0 |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
2 |
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
Результат имеет простой геометрический смысл – время процесса (перехода системы из одного состояния в другое) пропорционально площади под кривой 1/ x2 (x1 ). Чем выше проходит тра-
ектория x2 (x1 ) в верхней полуплоскости, а значит, чем больше скорость процесса, тем ближе кривая 1/ x2 (x1 ) к оси абсцисс, тем меньше ∆t , т.е. быстрее протекает процесс.
Рассмотрим пример фазовой траектории в виде отрезка прямой, направленной к началу координат (рис. 2.22, а).
Рис. 2.22. Фазовая траектория и переходный процесс
47
elib.pstu.ru

Уравнение отрезка прямой, направленной в начало координат
фазовой плоскости, имеет вид dx1 = x2 = − x1 . dt
Обратная кривая |
1 |
= − |
1 |
– это отрезок гиперболы, пло- |
x2 (x1 ) |
|
|||
|
|
x1 |
||
щадь под которой равна времени переходного процесса – прихода изображающей точки в начало координат.
Найдём это время:
0
∆t = − ∫ dx1 = − ln x1 0−1 = ∞ .
−1 x1
Действительно, прямолинейному отрезку фазовой траектории соответствует экспоненциальное движение (рис. 2.22, б), т.е. решение дифференциального уравнения отрезка при начальном условии x1 (0) = −1 имеет вид x1 (t) = −е−t .
Такое движение затухает бесконечно долго. Практически длительность прохождения изображающей точки на прямолинейном участке до отрезка (точки) покоя при достижении ею значения
(0,05–0,03).
Вычисление интервалов времени по координатам начальной и конечной точек оказывается затруднительным из-за вычисления площадей под ними. Чаще используют приближенный расчет интервалов времени по участкам фазовой траектории.
Пусть имеется фазовая траектория системы. Известно, что значение координаты x1 во времени будет следующим:
x1 = ∫t |
x2dt |
или ∆x1 = t∫2 x2dt . |
0 |
|
t1 |
Отсюда ∆x1 ≈ x2cp ∆t. |
|
|
Фазовая траектория аппроксимируется прямолинейными отрезками и определяются значения x2cp в середине каждого отрезка (рис. 2.23). Проекция этого отрезка на ось x1 даёт ∆x1. При этом
n
∆t = ∆ x1/ x2cp и t = ∑∆ti .
i=0
48
elib.pstu.ru
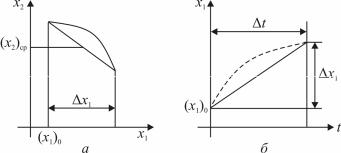
Рис. 2.23. Аппроксимация фазовой траектории прямолинейным отрезком (а) и начальный участок временной характеристики (б)
Аппроксимировав фазовую траекторию прямолинейными отрезками и вычислив интервалы времени для каждого ∆xi, можно построить временную характеристику.
49
elib.pstu.ru
3. МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
3.1. Общая характеристика метода гармонической линеаризации
Данный метод исследования получил распространение для исследования нелинейных систем автоматического управления высокого порядка (n > 2) с применением частотных представлений, используемых в теории линейных систем.
Сущность метода гармонического баланса заключается в замене нелинейного элемента эквивалентным безынерционным линейным, передаточный коэффициент которого не является постоянным, а зависит в общем случае от амплитуды и частоты искомых автоколебаний.
Метод позволяет исследовать возможность появления автоколебательных режимов, определить основные параметры автоколебаний (A, ωа), качественно оценить влияние нелинейностей на устойчивость и переходные процессы в системе, позволяет устранить автоколебания или же изменитьих параметры в желаемом направлении.
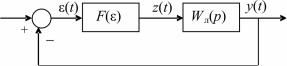
Рассматривается замкнутая автономная (без внешних воздействий) система с одним нелинейным элементом при ненулевых начальных условиях и с устойчивой или нейтральной линейной частью. Пусть в системе возможно возникновение автоколебаний, при этом z(t) – периодическая функция, содержащая спектр гармонических составляющих (рис. 3.1). Если при прохождении через линейную часть системы z(t) фильтруется так, что можно пренебречь всеми гармониками выше первой, то анализ системы можно вести методом гармонического баланса.
Рис. 3.1. Структурная схема нелинейной системы
50
elib.pstu.ru
