Теория автоматического управления. Нелинейные системы

Это предположение, называемое гипотезой фильтра, является необходимым условием применения метода гармонической линеаризации. Поскольку высшие гармоники по амплитуде обычно меньше, чем первая гармоника, и если линейная часть САУ узкополосная и в ней отсутствуют резонансные звенья, то во многих практических случаях гипотезафильтра выполняется, т.е. |W(jωa)| >>|W(jkωa)| при k >1.

Для приближённых расчётов условие гипотезы фильтра может быть сформулировано так: наклон ЛАЧХ линейной части должен быть по крайней мере от –20 до –40 дБ/дек на частоте автоколебаний ωа и должны быть выполнены неравенства:

– при наклоне ЛАЧХ –20 дБ/дек

– и при наклоне ЛАЧХ –40 дБ/дек

Поскольку данный метод является приближённым, то полученные результаты будут близки к истине только при выполнении определённых допущений:

1.Нелинейная система должна содержать только один нелинейный элемент с нечетно-симметричной (или приведенной к ней) статической характеристикой.

2.Линейная часть системы должна представлять собой фильтр низких частот, ослабляющий высшие гармоники.

3.Нелинейная система является автономной.

3.2. Комплексный коэффициент усиления (передачи) нелинейного элемента

Нелинейный элемент (НЭ) при действии на вход гармонического сигнала может быть описан комплексным коэффициентом усиления, зависящим от амплитуды входного сигнала.

51

elib.pstu.ru

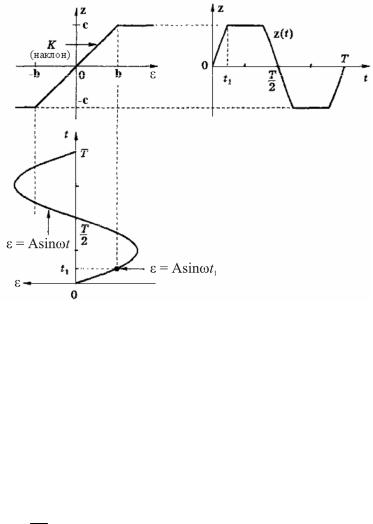
Будем рассматривать безынерционные нелинейные элементы с нечётно-симметричными статическими характеристиками (например, на рис. 3.2).

Рис. 3.2. Преобразование входного сигнала нелинейным элементом

Пусть на вход нелинейного элемента подаётся гармонический

сигнал ε(t) = A·sinωt (см. рис. 3.2), тогда выходная функция z(t) = = F(A·sinωt) является периодической (негармонической).

Разложим z(t) в ряд Фурье:

где при усреднении по фазе и замене ωt = ψ

2π

F0 = 21π ∫0 F(Asin ψ)dψ – постоянная составляющая выходной функции,

52

elib.pstu.ru

ставляющей z(t).

При условии выполнения гипотезы фильтра и симметричности статической характеристики НЭ ( F0 = 0 ) его выходной сигнал может быть представлен своей первой гармоникой:

Модуль и фазовый сдвиг комплексной функции, являясь соответственно амплитудой первой гармоники периодического выходного сигнала C1(A) и его сдвига по фазе θ(A), зависят от амплитуды входного гармонического сигнала.

– это коэффициенты гармонической линеаризации.

53

elib.pstu.ru

Преобразования по Лапласу выходной функции и входного воздействия имеют вид:

где р – оператор Лапласа.

По аналогии с линейным звеном свойства нелинейного элемента можно представить передаточным коэффициентом, назы-

ваемым эквивалентным комплексным передаточным коэффи-

циентом НЭ (эквивалентной передаточной функцией, коэффициентом гармонической линеаризации).

Определим эквивалентную передаточную функцию:

По преобразованию Фурье (при p = jω) получим эквивалентную частотную функцию, которая зависит от амплитуды входного сигнала:

Таким образом, нелинейный элемент может быть заменен линейным. Этот прием получил название гармонической линеари-

зации нелинейностей.

Если статическая характеристика НЭ нечетно-симметричная, то q'(A) = 0 , что показывает отсутствие фазового сдвига входного и

выходного сигналов.

3.3. Вычисление комплексных передаточных коэффициентов нелинейных элементов

В общем случае для динамических нелинейных элементов выходной установившийся периодический сигнал при гармоническом входном воздействии с конкретными значениями A и ω определя-

54

elib.pstu.ru

ется путём численного решения дифференциального уравнения. Затем находят значения коэффициентов гармонической линеаризации нелинейного элемента (приведены в табл. 3.1) по формулам усреднения по времени:

Эти формулы означают, что гармоническая линеаризация даёт усреднённые за период свойства нелинейного элемента по преобразованию гармонического сигнала. Повторяя эту операцию для разных ω, можно получить таблицу значений коэффициента гармонической линеаризации.

В частном случае безынерционных нелинейных элементов коэффициенты гармонической линеаризации от частоты ω не зависят. Эквивалентная передаточная функция, имеющая выражение

является функцией только амплитуды входных колебаний вида

WH (A) = q(A) + jq'(A) = RH (A)exp[ jθH (A)],

модуль и аргумент которой вычисляются как

Ниже приведен пример вычисления коэффициента гармонической линеаризации безынерционного элемента со статической характеристикой идеального двухпозиционного реле.

55

elib.pstu.ru

Рис. 3.3. Преобразование входного синусоидального сигнала идеальным релейным элементом

Вычислим коэффициенты гармонической линеаризации:

Эквивалентная передаточная функция идеального реле равна действительной части WН (А) = q(A) , а фазовый сдвиг θH (A) = 0 ,

т.е. фаза первой гармонической составляющей выхода совпадает с фазой входа (рис. 3.3).

График эквивалентной амплитудной характеристики показан на рис. 3.4, из которого видно, что малые по амплитуде сигналы проходят с большим усилением, а большие – с малым (дискриминация сигналов по уровню.

56

elib.pstu.ru