Теория автоматического управления. Нелинейные системы

1.5. Структурное преобразование нелинейной САУ к типовой

Преобразованием структурных схем можно привести нелинейную систему к системе с типовой структурой, а также заменой неоднозначных характеристик эквивалентной схемой из однозначной нелинейности в сочетании с линейными элементами обеспечить снижение порядка дифференциального уравнения системы.

На рис. 1.16 показаны этапы преобразования сложной структурной схемы нелинейной системы с использованием рассмотренных правил эквивалентности преобразований.

Рис.1.16. Пример преобразования структуры нелинейной системы

В результате преобразования получена «типовая» структурная схема с единичной отрицательной обратной связью и нелинейным элементом после элемента сравнения.

Влияние нелинейных элементов на характеристики нелинейных систем можно уменьшить:

1)улучшением конструкции функциональных элементов;

2)изменением параметров и структуры линейной части;

21

elib.pstu.ru

3)введением дополнительных линейных обратных связей (охватом нелинейных элементов линейной обратной связью);

4)компенсацией влияния нелинейностей (применением специальных компенсирующих нелинейных элементов, обеспечивающих линеаризацию системы);

5)введением дополнительных сигналов управления по отклонению;

6)применением вибрационной линеаризации нелинейностей.

22

elib.pstu.ru

2. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ

2.1. Основные понятия о методе

Метод фазовых траекторий представляет собой графоаналитический способ исследования нелинейных систем, сущность которого заключается в описании поведения системы при помощи наглядных геометрических представлений – фазовых портретов. Метод дает возможность получать наглядную и точную картину всей совокупности переходных процессов при любых начальных условиях для свободных колебаний.

Динамика нелинейных систем с выходной переменной в общем случае описывается с помощью нелинейного дифференциального уравнения

Данное уравнение можно представить в виде системы дифференциальных уравнений первого порядка:

Переменные xi (i =1,n) называются фазовыми переменными со-

стояния. Мгновенное состояние системы и ее дальнейшее поведение однозначно определены, если в некоторый момент времени t = t j из-

23

elib.pstu.ru

вестны значения всех n переменных xi . Эти значения можно рассматривать как координаты точек (x1 , x2 ,Kxn ) в n-мерном пространстве, которое называется фазовым пространством.

Точку с координатами (x1, x2 ,Kxn ) называют изображающей

точкой, а линию, по которой она перемещается при изменении состояния системы, – фазовой траекторией. Известно, что конкретному начальному состоянию системы (x1 (0), x2 (0),Kxn (0)) соответ-

ствует единственное решение системы (2.2) и, следовательно, единственная фазовая траектория. Поэтому множеству различных начальных условий соответствует семейство фазовых траекторий, которое называется фазовым портретом. Построение фазового портрета дает наглядное представление о поведении системы, в том числе предоставляет возможность определить режим автоколебаний.

Для систем высоких порядков фазовые портреты отображаются в многомерном пространстве, а для систем третьего и второго порядков – соответственно в пространстве и плоскости, что определяет практическую область применения данного метода.

Метод фазового пространства наиболее удобен в силу наглядности и простоты представления для анализа систем второго порядка, так как их фазовые траектории располагаются в фазовой плоскости переменных x1 и x2. Фазовый портрет этих систем можно построить непосредственно по дифференциальному уравнению, нерешая его.

Пусть описание системы представлено в виде нелинейного дифференциального уравнения второго порядка:

Данное уравнение можно представить в виде системы двух дифференциальных уравнений первого порядка

24

elib.pstu.ru

где x1 = x – отклонение выходной величины от установившегося значения. В качестве переменной x2 принята производная пере-

менной: x2 = dx1 . Разделив второе уравнение системы (2.4) на пер- dt

вое, можно получить уравнение фазовых траекторий в дифференциальной форме:

Решение данного дифференциального уравнения имеет уравнение фазовых траекторий в явном виде:

где C0 – постоянная интегрирования, зависящая от начальных ус-

ловий.

Из (2.6) видно, что каждой совокупности начальных условий x1(0), x2(0) соответствует свое решение и своя фазовая траектория.

2.2.Свойства фазовой плоскости

1.Из системы уравнений (2.4) следует, что в верхней полуплоскости изображающая точка движется всегда слева направо,

и движение по фазовой траектории происходит справа налево.

точек равновесия). Это означает, что в точках пересечения фазовых траекторий с осью x1 касательные к фазовым траекториям перпендикулярны к оси x1 , а переменная x1 достигает своего максимума.

3. При однозначной нелинейной функции в (2.5) каждой точке на фазовой плоскости (за исключением некоторых особых точек) соответствует только одно значение производной dx2/dx1, что озна-

25

elib.pstu.ru

чает, что фазовая плоскость состоит из семейства непересекающихся фазовых траекторий. Это позволяет получать наглядные и четкие представления о характере возможных движений, подобно суждению о магнитном поле по прохождению магнитных силовых линий на плоскости.

4.На фазовой плоскости имеется геометрическое место точек,

вкоторых наклон касательных ко всем фазовым траекториям одина-

ков (dx2/dx1 = const), называемых изоклинами. Изоклиной, общей для всех систем, является ось абсцисс фазовой плоскости (dx2/dx1 = ∞).

5.Если при x2 = 0 одновременно f2 (x1, x2 ) = 0 , то фазовая тра-

ектория в таких точках не имеет определенного направления, а обе

производные dx1 и dx2 равны нулю. Такие точки называются осоdt dt

быми. В особых точках по (2.4) обе производные равны нулю, что свидетельствует о неподвижности изображающей точки и нахождении исследуемой системы управления в состоянии равновесия. Особая точка, в которой начинаются все фазовые траектории, неустойчива.

6.Особые точки могут быть как реализуемыми физически, т.е. устойчивыми, так и неустойчивыми, в которых возможность прекращения движения существует только формально.

7.Геометрическое место точек на фазовой плоскости нелинейных систем, в которых происходит переход с одного вида фазовых траекторий на другой, называется линией переключения.

2.3.Фазовые портреты линейных систем 2-го порядка

Проведем анализ фазовых портретов линейных систем второго порядка:

Характеристическое уравнение, корни которого определяют характер переходных процессов в системе (уравнение свободных колебаний), приведем к виду

26

elib.pstu.ru

где h – коэффициент демпфирования; ω0 – частота собственных колебаний.

Вид фазовых траекторий существенно зависит от корней характеристического уравнения:

Уравнение фазовой траектории определяем из решения системы уравнений 1-го порядка:

На рис. 2.1–2.4 приведены фазовые портреты линейных систем второго порядка и соответствующие им переходные процессы. На фазовых портретах данных систем изоклинами являются прямые, проходящие через начало координат, что видно из (2.10):

где χ – коэффициент наклона касательной к фазовой траектории при пересечении ее с изоклиной.

Для всех фазовых траекторий изоклинами вертикальных касательных к фазовым траекториям является ось абсцисс x2 = 0.

На рис. 2.2 ось ординат пересекается фазовыми траекториями с χ = –2h, а изоклина горизонтальных касательных к фазовым траекториям показана с χ = 0.

В зависимости от параметров h и ω переходный процесс в линейной системе 2-го порядка может иметь вид:

–периодических колебаний;

–затухающих или расходящихся колебаний;

–монотонного, апериодического затухающего или расходящегося процессов.

Так, например, решение уравнения (2.10) при h = 0 (мнимых сопряженных корнях характеристического уравнения) даст фазовые траектории с уравнением эллипса, фазовый портрет системы –

27

elib.pstu.ru

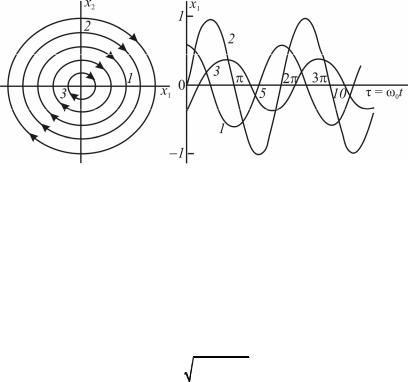
ввиде семейства вложенных концентрических эллипсов с центром

вначале координат с полуосями b⁄a= ω0. В частном случае, когда b = a, фазовый портрет представляется семейством окружностей (рис. 2.1), а переходный процесс оказывается незатухающим коле-

бательным с частотой ω0. Начало координат является особой точкой фазовой плоскости типа центр.

Рис. 2.1. Фазовый портрет и переходные процессы при h = 0

В случае, если ω02 > h2, корни характеристического уравнения (2.9) являются комплексными сопряженными. Переходные процессы для этих случаев, представленные на рис. 2.2, а и 2.2, б, соответствуют устойчивой и неустойчивой системам.

Фазовые траектории соответствуют логарифмической спирали:

При h > 0 фазовые траектории оказываются скручивающимися кначалу координат и расходящимися из начала координат при h < 0. На фазовой плоскости особыми точками являются устойчивый и не-

устойчивый фокусы.

При ω02<h2 корни характеристического уравнения (2.9) оказываются действительными, причем при h > 0 являются отрицательными, что соответствует устойчивой системе, и положительными

28

elib.pstu.ru

при h < 0, соответствующими неустойчивой системе с расходящимися фазовыми траекториями. Фазовые портреты для данных случаев приведены на рис. 2.3 с особыми точками типов устойчивый и неустойчивый узел.

Рис. 2.2. Фазовые портреты и переходные процессы при ω02 > h2: а при h > 0, б при h < 0

На фазовых портретах данных систем имеются по 2 изоклины, являющиеся одновременно фазовыми траекториями, показанными с индексами χ1 и χ2. Действительно, пусть x2 = χ· x1, тогда для него

dx2 ⁄ dx1 = x2/ x1 = χ.

Подставляя это соотношение в (2.10), получаем χ = – ω02/χ – h2, откуда χ2 + 2hχ + ω02 = 0, т.е. угловой коэффициент луча является корнем характеристического уравнения системы.

29

elib.pstu.ru