
Теория автоматического управления. Нелинейные системы
.pdf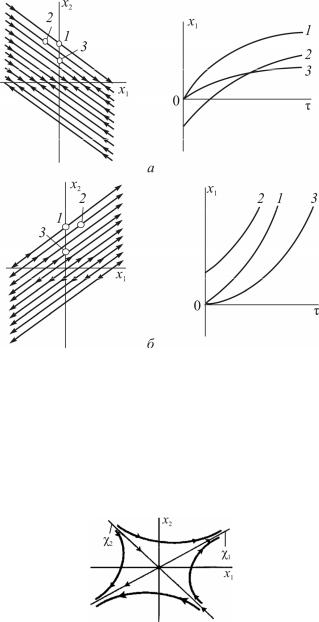
Рис. 2.4. Фазовые портреты и переходные процессы при ω02= 0: а при h > 0, б при h < 0
Фазовый портрет системы обладает, как и в случае ω02 < h2, двумя изоклинами, являющимися в то же время фазовыми траекториями (χ1 и χ2), которые разделяют фазовую плоскость на области с различным видом фазовых траекторий. Эти особые фазовые траектории называют сепаратрисами. Точкой равновесия системы является седло. Фазовый портрет системы показан на рис. 2.5.
Рис. 2.5 Фазовый портрет с особой точкой типа седло
31
elib.pstu.ru
Свойства фазовых траекторий для линейных систем сохраняются и для фазовых траекторий нелинейных систем. Однако фазовые траектории нелинейных систем имеют свои особенности.
2.4.Особенности нелинейных систем
Вфазовых пространствах нелинейных систем в отличие от линейных может быть несколько особых точек, относящихся к устойчивым и неустойчивым точкам равновесия (даже отрезкам равновесия).
Топологическая структура фазовых пространств нелинейных систем в отличие от линейных разделена на ряд областей. В нелинейных системах наблюдаются более сложные движения, не всегда поддающиеся математическому описанию. Некоторые из этих режимов принципиально невозможны в линейных системах. Примером такого движения является автоколебательный режим, описываемый на фазовой плоскости периодическим движением изображающей точки по некоторой замкнутой кривой, называемой предельным циклом. На примерах фазовых портретов (рис. 2.6) предельные циклы выделены жирными линиями, режиму автоколебаний соответствует фазовый портрет, на котором фазовые траектории сходятся к предельному циклу или расходятся от него. На рис. 2.6, а положение равновесия устойчиво «в большом». Область «притяжения точки покоя» ограничена неустойчивым предельным циклом. При этом следует отметить, что замкнутая кривая не может наблюдаться физически, например на осциллографе. Неустойчивый предельный цикл – математическая абстракция. На рис. 2.6, б предельный цикл является устойчивым, так как в системе при любых начальных условиях имеют место автоколебания.
На рис. 2.6, в устойчивая точка равновесия окружена двумя предельными циклами: внутренним неустойчивым и внешним устойчивым.
Как видно по фазовым траекториям, если начальные условия находятся вне внутреннего предельного цикла, ограниченного заштрихованной областью, в системе возникают автоколебания, обусловленные предельным циклом. Областью притяжения внешнего предельного цикла является вся фазовая плоскость за исключением области устойчивости положения равновесия (х1 = 0, x2 = 0).
32
elib.pstu.ru
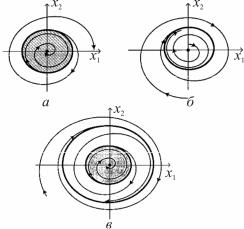
Рис. 2.6. Фазовые портреты с предельными циклами
Область начальных условий, определяющая понятия устойчивости «в малом» и «в большом», приведена ниже в разделе устойчивости систем.
2.5. Исследование динамики нелинейных систем
Статические характеристики нелинейных звеньев на отдельных участках описываются линейными уравнениями либо приближенно могут описываться совокупностью линейных уравнений, сопрягаемых в определенных точках. Поэтому построение фазовых траекторий таких систем сводится к их построению для различных линейных систем и сопряжению в точках перехода от одного линейного участка к другому.
2.5.1. Многолистная фазовая плоскость
Каждый участок фазовой плоскости, соответствующий одному линейному участку нелинейной характеристики, называют листом фазовой плоскости. На каждом листе многолистной фазовой плоскости динамика системы будет описываться линейным дифференциальным уравнением, правая часть которого const.
33
elib.pstu.ru
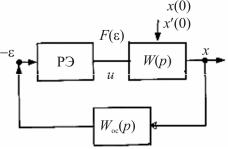
Рассмотрим конструирование многолистной фазовой плоскости на примере релейной следящей системы с различными типами реле (рис. 2.7), широко используемыми в технике.
Рис. 2.7. Структурная схема релейной следящей системы
Пусть дифференциальное уравнение объекта вместе с исполнительным устройством в общем случае имеет вид:
a |
d 2 x(t) |
+ a |
dx(t) |
+ a |
|
x(t) = кu(t), |
(2.13) |
dt2 |
|
|
|||||
0 |
1 |
dt |
2 |
|
|
||
где a0 > 0, a1 ≥ 0, a2 ≥ 0, к ≥ 0, u(t) = F(ε, t).
Согласно ограничениям на коэффициенты передаточная функция W(p) может содержать только устойчивые и нейтральные звенья.
В качестве регулятора в системе используется безынерционный релейный элемент (симметричный), у которого F(ε, t) = const и который может принимать значения в общем случае –с, 0, +с.
На структурной схеме системы показаны начальные условия, т.е. исходное состояние объекта х0, x′0, определяющие режим свободного движения.
Пусть в системе применена жесткая единичная отрицательная
обратная связь (Wос(p) = 1).
Рассмотрим случай с двухпозиционным идеальным реле со статической характеристикой на рис. 1.6. На рис. 2.8, б показаны листы фазовой плоскости, соответствующие частям, когда сигналы реле равны +c и –с. Эти части фазовой плоскости называются листами «+c» и «–с». При наложении листов на исходную фазовую плоскость
34
elib.pstu.ru
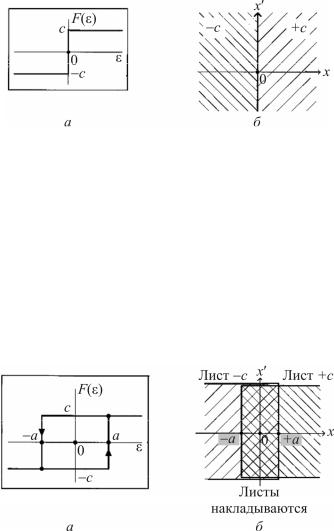
границы листов сомкнутся. Переход изображающей точки с одного листа на другой происходит по границе листов. В данном случае на фазовой плоскости линией переключения является ось ординат.
Рис. 2.8. Листы фазовой плоскости системы с идеальных двухпозиционных реле
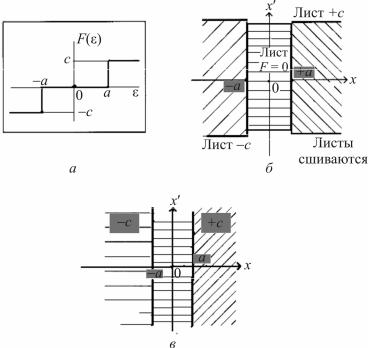
При наличии у реле гистерезиса, статическая характеристика которого приведена на рис. 1.7, листы +с и –с наложатся друг на друга. Поскольку переход изображающей точки с листа на лист определён двумя условиями:
1)|x| = a,
2)направление переключения реле однозначно определяется знаком производной dx/dt, переход с одних фазовых траекторий на другие в верхней полуплоскости происходит при х = а, а в нижней – при х = – а (рис. 2.9).
Рис. 2.9. Листы фазовой плоскости системы с реальным двухпозиционным реле
35
elib.pstu.ru
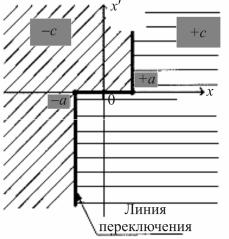
Рис. 2.10. Линия переключения на двухлистной фазовой плоскости
Линия переключения на фазовой плоскости для данного случая показана на рис. 2.10.
Если реле имеет три позиции статической характеристики +с, 0,
–с, показанные на рис. 1.8, структура фазовой плоскости дополняется еще одним листом. Наличие нечувствительности реле приводит к трёхлистной фазовой плоскости, приведенной на рис. 2.11, б. В отличие от предыдущего случая фазовая плоскость разделена на 3 области линиями переключения х = + a, х = – a, показанными на рис. 2.11, в, так как фазовые траектории переходят от одного вида к другим при переключениях реле независимо от знака скорости изменения выходной переменной системы.
Если трехпозиционное реле обладает гистерезисом статической характеристики, линии переключения отличаются от показанных на рис. 2.11, в. Отрезок покоя (равновесия системы) при этом уменьшается на 2 значения ширины гистерезиса (рекомендуется построить самостоятельно).
В следящих системах, имеющих воздействие по производной (параллельную гибкую обратную связь) наряду с жесткой отрицательной обратной связью с передаточной функцией звена
36
elib.pstu.ru
Wос(p) = E(p)/X(p) = αp + 1, |
(2.14) |
линии переключения на фазовой плоскости будут определяться уравнениями:
для идеального двухпозиционного реле
αx′ + x = 0 |
(2.15) |
и для идеального трёхпозиционного реле |
|
αx′ + x = ± a. |
(2.16) |
Рис. 2.11. Фазовая плоскость системы с трехпозиционным реле: а – листы фазовой плоскости, б – линия переключения
Это означает, что воздействие по производной приводит к наклону границ листов в соответствии с соотношениями (2.15) и (2.16) в положительном направлении.
37
elib.pstu.ru

Наличие запаздывания в структуре линейной части системы вызывает опоздание переключений реле на время τ. В течение промежутка времени τ изображающая точка будет двигаться по старой траектории, таким образом, запаздывание не изменит формы фазовых траекторий на листах, но деформирует вправо линии переключения изображающей точки с одного листа на другой, что, разумеется, может приводить к новым явлениям (по сравнению с тем случаем, когда запаздывание отсутствует), например, к возникновению автоколебаний.
2.5.2. Исследование релейной системы управления
объектом с W ( p) = k p2
Исследование динамических свойств релейных следящих систем проведем вначале на примере идеального объекта управления.
Дифференциальное уравнение системы имеет вид в соответствии с рис. 2.7
d2x/dt2 = –kF(x).
Составим из (2.17) систему уравнений,
dx1/dt = x2,
dx2/dt = –kF(x1).
(2.17)
введяобозначение x = x1:
(2.18)
Исключив время из системы (2.18), получим уравнение фазовых траекторий в дифференциальной форме: dx2/dx1 = –kF(x1)/x2, решением которого является
|
x22 − x202 = 2(x1 |
− x0 ) / kF (x1 ) |
(2.19) |
|
|
|
|
|
|
или |
x1 = x22 |
2kF (x1 ) + C, |
(2.20) |
|
|
|
|
||
где С – постоянная интегрирования.
Фазовые траектории описываются уравнениями парабол, располагаемых вдоль оси абсцисс (для различных начальных условий), кривизна которых определена параметрами системы.
38
elib.pstu.ru
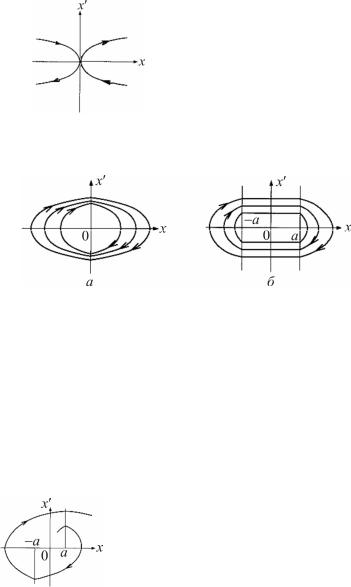
Рис. 2.12. Фазовые траектории системы управления с объектом управления
из двух интегрирующих звеньев
На рис. 2.12 приведены фазовые траектории при С = = 0, слева от оси х' = x2 для
F(x) = +c, справа – F(x) = –c.
Фазовый портрет нелинейной системы с идеальным двухпозиционным реле показан на рис. 2.13, а и с идеальным трёхпозиционным– нарис. 2.13, б.
Рис. 2.13. Фазовые портреты системы 2-го порядка:
а– с идеальным двухпозиционным реле;
б– с идеальным трехпозиционным реле
Вобоих случаях фазовый портрет представляет собой бесконечное семейство вложенных друг в друга замкнутых кривых. Динамические режимы в системах не являются предельными циклами (режимы соответствуют системе с идеальными характеристиками линейной части и нелинейного элемента), параметры которых определены начальными условиями.
Фазовая траектория системы с реальным двухпозиционным реле (с гистерезисом) показана на рис. 2.14.
Рис. 2.14. Фазовая траектория системы с реальным двухпозиционным реле
Как видно из рис. 2.14, независимо от начальных условий изображающая точка переходит на линиях переключения x = a и x = –a на фазовые траектории в виде парабол (см. рис. 2.12) с фокусами, удаляющимися от начала координат. Динамический режим в системе в данном случае соответствует расходящимся колебаниям.
39
elib.pstu.ru
Рассмотрим случай, когда имеет место воздействие по производной, т.е. звено обратной связи описывается передаточной функцией, приведенной в (2.14).
Пусть в системе нелинейный элемент имеет статическую характеристику идеального двухпозиционного реле. Линия переключения определяется из условия ε = 0.
Тогда уравнение линии переключения имеет вид
х′ = –х/α. |
(2.21) |
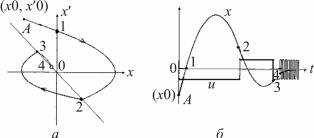
В этом случае линии переключения повернутся в положительном направлении. На рис. 2.15, а показана фазовая траектория системы, описываемой уравнением (2.17) с идеальным двухпозиционным реле и обратной связью по уравнению (2.14). Начальные условия системы соответствуют точке А фазовой плоскости. Переключения реле и соответствующие им моменты времени показаны на рис. 2.15, б.
Рис. 2.15. Скользящий режим в нелинейной системе: а – фазовая траектория; б – временные характеристики
Начиная с точки 4, изображающая точка движется к началу координат фазовой плоскости вдоль линии переключения.
С момента времени t4, как видно из рис. 2.15, б, возникает качественно новый динамический режим системы, называемый
«скользящим».
На рис. 2.16 показано условие возникновения «скользящего режима». На фазовой плоскости линия переключения системы MN касается двух фазовых траекторий, показанных пунктирными линиями, в точках А и В.
40
elib.pstu.ru
