
Теория расчет и проектирование авиационных двигателей и энергетичес.-1
.pdfчем T c в двигателе без ФК, то есть в ТРДФ существенно возрастают потери тепла с выходящими газами: ↑↑Q2 = = cp (↑↑Тс.ф −Тн ) .
Lц.ф max, |
следовательно, ηt ф max |
достигается при давлении |
||||||
за турбиной |
pт.ф. опт , соответствующем полной степени рас- |
|||||||
ширения газа в РС (πс.расп = πс.п ). |
|
|
|
|
|
|
||
Если при Тт.ф = const , то есть QФК = const, увеличивать |
||||||||
π , то будет расти p |
↑ L |
↑ η |
. При π |
= π |
дав- |
|||
дв |
т.ф |
ц.ф |
|
tф |
|
дв |
опт |
|
ление за турбиной р |
L |
|
η |
|
. |
|
|
|
|
т.ф.опт |
ц.ф max |
t ф max |
|
|
|
||
При дальнейшем росте πдв > πопт работа цикла Lц.ф будет
уменьшаться, следовательно, будет снижаться ηtф.
Таким образом, у ТРДФ, в отличие от ТРД, значение ηt ф max достигается при оптимальной степени повышения давления.
3.3.Реальные (действительные) циклы ВРД
3.3.1.Процессы в действительном цикле
Вдействительном цикле ВРД:
–все процессы сопровождаются потерями энергии;
–физические свойства рабочего тела, характеризуемые
параметрами k, ср, R, изменяются при изменении температуры в процессах сжатия-расширения и подвода тепла, а также при изменении химического состава газа в КС.
Например, при сжатии воздуха в реальном ВЗ процесс повышения давления – политропный (рис. 3.7), то есть из-за
наличия гидравлического сопротивления |
(трения |
воздуха |
о стенки ВЗ) температура возрастает с T |
до Т |
, следо- |
вх.ад |
вх.п |
|
вательно, возрастает энтропия. Для сжатия более нагретого
91
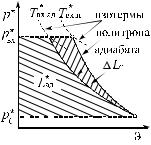
Рис. 3.7. Работа сжатия в ВЗ
газа до давления рвх необходимо
затратить бóльшую (политропную)
работу Lп = Lад + ∆Lr, где ∆Lr – тепловое сопротивление;
|
|
|
k |
|
|
|
|
|
p |
|
k −1 |
|
|
||||
|
|
|
|
|
|
|
|
|
k |
|
|
||||||
L |
= |
|
|
|
|
|
RT |
|
вх |
|
|
−1 |
; (3.13) |
||||
|
k −1 |
p |
|
||||||||||||||
ад |
|
|
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|||
|
|
|
n |
|
|
|
|
p |
n |
|
|
||||||
L |
= |
|
|
|
RT |
|
|
|
вх |
|
|
|
−1 . |
(3.14) |
|||
n −1 |
|
р |
|
||||||||||||||
п |
|
|
|
0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Показатель политропы n в данном примере зависит от температуры газа и всегда n > k (для ВЗ ВРД n ≈ 1,5…1,54).
Помимо того, что необходима дополнительная работа для сжатия более нагретого при преодолении гидравлического сопротивления газа, необходима дополнительная работа Lr для преодоления трения воздуха о стенки канала ВЗ. Следовательно, полная работа, потребная на сжатие воздуха в ВЗ,
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
k |
|
|
p |
n |
|
|
||
L |
= L |
+ L |
= |
|
|
RT |
|
вх |
|
−1 . |
(3.15) |
|
k −1 |
р |
|||||||||||
ВЗ |
п |
r |
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как полная работа LВЗ совершается за счет изменения кинетической энергии воздуха в ВЗ:
|
L = |
V 2 −c2 |
|||
|
|
|
вх |
, |
|
|
|
|
|||
|
ВЗ |
|
2 |
|
|
то |
|
|
|
||
|
|
|
|
||
V 2 −с2 |
|
|
|
|
|
|
вх |
= L |
+ L . |
||
|
|
||||
2 |
|
п |
|
r |
|
|
|
|
|
||
(3.16)
(3.17)
Изменение кинетической энергии в реальных ВЗ расходуется на политропную работу сжатия (с учетом дополни-
92
тельного подогрева при трении) и преодоление гидравлического сопротивления.
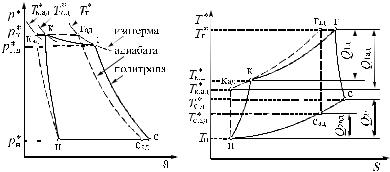
Сравним диаграммы идеального и действительного циклов ТРД (рис. 3.8, 3.9) при условии, что Σπдв.д = ∑ πдв.ид ;
(Тг  Тн )д = (Тг
Тн )д = (Тг  Тн )ид .
Тн )ид .
Рис. 3.8. Действительный |
Рис. 3.9. Действительный цикл |
цикл ТРД в координатах р–ϑ |
ТРД в координатах Т–S |
На диаграммах обозначено:
н–к – политропное сжатие воздуха. Потребная работа сжатия рабочего тела (воздуха) в действительном цикле (в сравнении с адиабатным) больше на величину ∆Lr и Lr, а температура за ОК Tк.д выше, чем Tк ;
к–г – подвод тепла к рабочему телу в КС. В действительном цикле идет не при постоянном давлении, так как в КС имеют место потери полного давления. Следовательно, перед ГТ газ имеет меньшее давление pг.д и меньшую пол-
ную энергию (работоспособность); г–с – расширение газа в ГТ и РС. В реальном цикле про-
цесс расширения газа политропный, поэтому температура на срезе РС Тс.д выше, чем Тс .
93
Для подогрева газа до заданной T |
в действительном |
||
|
г |
|
|
цикле необходимо подвести |
меньше тепла Q1д, так |
как |
|
(Тг −Тк.д ) <(Тг −Тк.ад ) . Газы |
покидают |
двигатель |
при |
Тс*.д >Тс*.ад (при одной и той же суммарной степени пониже-
ния давления газ дополнительно подогревается от трения),
следовательно, Q2д > Q2ад.
Работа действительного цикла меньше работы идеального цикла:
Lц.д = Q1д – Q2д < Lц.ад = Q1ад – Q2ад. |
(3.18) |
3.3.2.Работа действительного цикла ТРД
Вдействительном цикле ТРД часть работы цикла идет на преодоление механических и гидравлических сопротивлений и не участвует в приращении скорости газа (создании тяги).
Внутренняя (индикаторная) работа
Внутренней работой действительного цикла называется работа, эквивалентная площади цикла, которая, как видно на рис. 3.8, соответствует разности полезных политропных работ в процессах расширения и сжатия:
Lвн = Lп.р – Lп.с. |
(3.19) |
Запишем уравнение Бернулли для процесса сжатия 1 кг воздуха в ТРД
L + |
V 2 |
−c2 |
= L |
+ L . |
|
|
к |
(3.20) |
|||
|
|
||||
к |
|
2 |
п.с |
rc |
|
|
|
|
|
|
Работа, подводимая к воздуху в компрессоре, и изменение кинетической энергии воздуха при его торможении от
94
скорости V до скорости ск расходуется на политропное сжатие воздуха в ТРД Lп.с и на преодоление его гидравлических потерь в процессе сжатия Lrс.
Принимая допущение, что расходы газа и воздуха равны (Мг = Мв), запишем уравнение Бернулли для процесса расширения 1 кг газа в ТРД от сечения к до сечения с:
|
|
с2 |
−с2 |
|
|
|
L |
= L + |
с |
к |
+ L |
. |
(3.21) |
|
|
|||||
п.р |
т |
|
2 |
rр |
|
|
|
|
|
|
|
|
Полезная работа, совершаемая при политропном расширении газа в ТРД, расходуется на вращение турбины Lт, увеличение кинетической энергии газа и преодоление гидравлических потерь в процессе расширения Lrp.
Подставим в уравнение (3.19) выражения Lп.с и Lп.p из уравнений (3.20) и (3.21) и получим
|
с2 |
−V 2 |
|
|
|
|
|
L = |
с |
|
+ L |
− L |
+ L |
+ L . |
(3.22) |
|
|
||||||
вн |
|
2 |
т |
к |
rс |
rp |
|
|
|
|
|
|
|
|
Работа газовой турбины у ТРД расходуется на привод компрессора и привод дополнительных агрегатов, то есть Lт – Lк = Lм, где Lм – механическая работа привода агрегатов.
Тогда
|
с2 |
−V 2 |
|
|
|
L = |
с |
|
+ L |
+ΣL . |
(3.23) |
|
|
||||
вн |
|
2 |
м |
r |
|
|
|
|
|
|
Внутренняя (индикаторная) работа расходуется на приращение кинетической энергии по тракту двигателя на привод агрегатов и преодоление всех гидравлических сопротивлений.
Эффективная работа цикла ТРД
Под эффективной работой цикла ТРД понимают работу, затраченную на приращение кинетической энергии рабочего тела по тракту ТРД:
95
L = |
c2 |
−V 2 |
= L |
−(ΣL + L |
) . |
|
|
c |
|
(3.24) |
|||||
|
|
||||||
е |
|
2 |
вн |
r |
м |
|
|
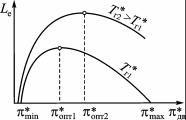
Характер зависимости Le (πдв, Тг ) определяется изме-
нением внутренней работы цикла Lвн и величины потерь при изменении πдв и Тг (рис. 3.10).
Рис. 3.10. Зависимость
Lе (πдв, Тг )
При πдв = πmin вся получаемая работа цикла Lвн расходуется на преодоление суммарных гидравлических потерь и привод агрегатов, следовательно, Lе = 0.
При πmin < πдв < πопт изза улучшения теплоисполь-
зования в ТРД (↓Тс ↓Q2 ) темп роста Lвн превосходит
темп роста гидравлических потерь, следовательно, увеличивается Lе.
При увеличении πдв > πопт Lвн начинает уменьшаться
вследствие более энергичного снижения подводимой тепло- |
||||||
ты |
Q = c |
p |
(Т −↑↑Т ) |
по сравнению со снижением |
||
|
1 |
г |
к |
|
|
|
Q =(↓T −T ) . Одновременно при увеличении π |
продол- |
|||||
2 |
c |
|
н |
|
дв |
|
жают расти гидравлические потери, поэтому, пройдя максимум при πдв = πопт , Lе начинает снижаться.
При πдв = πmax внутренняя работа цикла становится
равна возросшей суммарной работе, потребной на преодоление гидравлических потерь и привод агрегатов (Lвн = ΣLr + + Lм), следовательно, Le = 0.
Увеличение Тг при πдв = const ведет к росту величины подведенного к газу тепла Q1 = cp (↑Тг −Тк ) , следовательно,
96
увеличению Lвн. Так как гидравлические потери в процессах сжатия и расширения не изменяются (πдв = const) , а тепло-
вые потери в КС возрастают незначительно, то Le будет расти
(см. рис. 3.10).
Одновременно снижение в Lвн доли работы, потребной на преодоление потерь, приведет к более позднему достижению πопт и πmax .
3.3.3. Эффективный КПД ТРД
Эффективный КПД ηe показывает, какая часть тепла Q1, подведенного к рабочему телу в двигателе, преобразуется в эффективную работу цикла:
η = |
Le |
=1− |
1 |
|
, |
(3.25) |
|
n−1 |
|||||
e |
Q1 |
|
|
|
||
|
|
πдв |
n |
|
|
|
|
|
|
|
|
||
где n – показатель политропы.
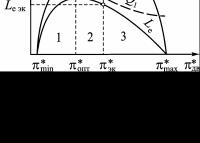
Зависимость ηe (π*дв, Tг* )
Изменение ηe при изменении πдв (рис. 3.11) оп-
ределяется взаимным изменением Le и Q1. При увеличении πдв увеличивается
температура воздуха за компрессором Тк , следова-
тельно, уменьшается количество тепла, подводимого
к |
газу |
в |
камере |
сгорания Рис. 3.11. Зависимость η |
(π |
) |
|
↓Q = c |
|
|
e |
дв |
|
||
p |
(Т −↑Т ) . |
|
|
||||
|
1 |
|
г |
к |
|
|
|
97

1.При πmin < πдв < πопт
↑↑ηe = ↑ Le .
↓Q1
2.При πопт < πдв < πэк
↑ηе = ↓↓↓ LQe1 .
3.При πэк < πдв < πmax
↓ηe = ↓↓ Le .
↓Q1
При πдв = πэк ηe достигает максимального значения (потери тепла минимальны), то есть удельный расход топлива минимальный (cR min). На рис. 3.11 видно, что πэк не совпадает с πопт, поэтому при выборе значения πдв приходится идти на компромисс – получить Lе max (πопт ), следовательно, мак-
симальную тягу, или максимальную экономичность cR (πэк ) .
При πдв = const с увеличением Тг растет Le. Так как по-
тери в процессах сжатия и расширения остаются неизменными, то доля подведенной теплоты Q1, идущая на совершение эффективной работы Le, возрастает, и это приводит к росту
эффективного КПД ηe = ↑↑ Le (рис. 3.12).
↑Q1
Снижение в Lвн доли работы, потребной для преодоления потерь ΣLr, приведет к более позднему достижению πoпт и, следовательно, πэк .
98

Рис. 3.12. Зависимость ηe (Тг )
Зависимость ηe от высоты полета Н
При увеличении высоты полета H температура атмосферного воздуха Тн уменьшается, следовательно, уменьшаются полная температура воздуха на входе в двигатель Твх
и температура |
за компрессором |
Тк . Одновременно при |
||
уменьшении Т |
увеличивается n |
~ |
n |
, следовательно, |
|
||||
|
||||
вх |
пр |
|
↓Твх |
|
|
|
|
|
|
увеличивается πк и Тк . Рост πк оказывает сдерживающее действие на темп уменьшения Тк .
Если двигатель работает на установившемся режиме (Тг = const), то при уменьшении Тк интенсивно увеличивается степень подогрева газа в КС, то есть увеличивается ко-
личество тепла, |
подведенного |
к газу в |
КС: ↑↑Q1 = |
= сp (Тг −↓Тк ) и |
увеличивается |
внутренняя |
работа цикла |
(↑↑ Lвн ) . |
|
|
|
Величина потерь с ростом высоты полета возрастает незначительно, так как при ↓Тн ↓Твх ↑ πк ↑ ∑ Lr , поэто-
99

му при увеличении Q1 увеличивается относительная доля Le во внутренней работе цикла, следовательно, увеличивается эффективный КПД ηe =
=↑↑ Le  ↑Q1 (рис. 3.13).
↑Q1 (рис. 3.13).
Начиная с H = 11 км, температура воздуха с ростом высоты не изменяется, следова-
Рис. 3.13. Зависимость ηe(H) тельно, Le и Q1 не изменяются, и эффективный КПД ηе также
не изменяется (ηе = const).
Зависимость ηe от числа М полета
При увеличении скорости полета (↑ M) полная темпе-
ратура воздуха на входе в двигатель Твх увеличивается, следовательно, увеличивается температура за компрессором Тк .
Одновременно, при увеличении |
Твх |
уменьшается |
||||
n ~ |
n |
|
, следовательно, уменьшается π |
и Т . Умень- |
||
|
|
|||||
|
|
|||||
пр |
|
↑Твх |
к |
к |
||
|
|
|
|
|||
шение πк |
оказывает сдерживающее действие на темп роста |
|||||
Тк . |
|
|
|
|
|
|
|
Если двигатель работает на установившеемся режи- |
|||||
ме(Тг = const) , то при увеличении Тк |
интенсивно уменьша- |
|||||
ется степень подогрева газа в КС, то есть уменьшается количество тепла, подведенного к газу в КС: ↓↓Q1 = сp (Тг −↑Тк ) , следовательно, существенно снижается внутренняя работа цикла(↓↓ Lвн ) .
100
