
Сопротивление материалов. Примеры решения типовых задач
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
Т.В. Чернова
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Утверждено Редакционно-издательским советом университета
в качестве учебно-методического пособия
Издательство Пермского национального исследовательского
политехнического университета
2015
УДК 620.10 (072.8) Ч-49
Рецензенты:
д-р техн. наук, профессор Г.Л. Колмогоров (Пермский национальный исследовательский политехнический университет);
канд. физ.-мат. наук, доцент И.Э. Келлер (Институт механики сплошных сред УрО РАН, г. Пермь)
Чернова, Т.В.
Ч-49 Сопротивление материалов. Примеры решения типовых задач : учеб.-метод. пособие / Т.В. Чернова. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2015. – 96 с.
ISBN 978-5-398-01517-1
Представлены темы практических занятий по курсу «Сопротивление материалов». Основное внимание уделено методикам решения практических задач по рассматриваемым темам курса, приведены основные расчетные формулы и примеры решения типовых задач, задания для самостоятельного решения, а также вопросы для самопроверки.
Предназначено для студентов очной формы обучения по направлению 15.03.03 (151600.62) «Прикладная механика» (по профилям: 03 – «Вычислительная механика и компьютерный инжиниринг»; 04 – «Динамика и прочность машин, приборов и аппаратуры»; 05 – «Компьютерная биомеханика»).
УДК 620.10 (072.8)
ISBN 978-5-398-01517-1 |
© ПНИПУ, 2015 |
|
ОГЛАВЛЕНИЕ |
|
Общие указания к выполнению и оформлению |
|
|
индивидуальных заданий............................................................................ |
4 |
|
Перечень тем практических занятий.......................................................... |
5 |
|
Тема 1. Расчет стержней при косом изгибе............................................... |
6 |
|
Тема 2. Расчет на прочность при циклическом нагружении................. |
18 |
|
Тема 3. Определение перемещений методом Мора ............................... |
28 |
|
Тема 4. Расчет статически неопределимых стержневых |
|
|
систем методом сил ................................................................................... |
42 |
|
Тема 5. |
Расчет движущихся систем с учетом сил инерции .................. |
62 |
Тема 6. |
Расчеты на удар ........................................................................... |
67 |
Тема 7. |
Расчеты на устойчивость продольно сжатых стержней........... |
75 |
Список литературы.................................................................................... |
89 |
|
Приложение ............................................................................................... |
90 |
|
3
ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Каждый студент по теме практического занятия получает индивидуальное задание. Расчетные схемы и числовые данные для каждой работы выбираются по шифру, выдаваемому преподавателем.
Задания по дисциплине «Сопротивление материалов» являются самостоятельной работой студентов по практическому применению основных теоретических положений курса с целью углубленного освоения программного материала, приобретения навыков выбора методик решения поставленных задач и проведения инженерныхрасчетов, пользования справочнойлитературой.
Индивидуальные задания оформляются в отдельной тетради в виде пояснительной записки, которая включает: титульный лист с обязательным указанием темы задания, шифра задания; расчетную часть; графическое построение (с обязательным соблюдением масштаба).
Расчетная часть должна состоять из исходных данных и расчетной схемы или эскиза с указанием всех необходимых для расчета величин в соответствии с шифром задания. Нужно помнить, что необходимая информация для решения задачи дается, как правило, начертежах, поэтому ихнужновыполнятькрайнеаккуратно.
Каждый этап работы нумеруется и снабжается заголовками в соответствии с пунктами, указанными в содержании работы, необходимыми пояснениями и схемами. При выполнении расчетов сначала необходимо записывать выражения в общем виде, далее при определении из формул численного значения какой-либо величины подставляют численные значения всех букв, затем приводят результаты без промежуточных выкладок. Указание всех размеров, а также размерностей всех величин обязательно. Работы, оформленные небрежно и без соблюдения предъявляемых к ним требований, не рассматриваются. Работы выполняются в срок, предусмотренный учебным планом.
4
ПЕРЕЧЕНЬ ТЕМ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
1.Расчет стержней при косом изгибе.
2.Расчет на прочность при циклическом нагружении.
3.Определение перемещений методом Мора.
4.Расчет статически неопределимых стержневых систем методом сил.
5.Расчет движущихся систем с учетом сил инерции.
6.Расчеты на удар.
7.Расчеты на устойчивость продольно сжатых стержней.
5
ТЕМА 1. РАСЧЕТ СТЕРЖНЕЙ ПРИ КОСОМ ИЗГИБЕ
Сложным сопротивлением называется такой общий случай нагружения бруса внешними нагрузками, когда в его поперечных сечениях возникает сразу несколько внутренних силовых факторов: продольные и поперечные силы, крутящий и изгибающие моменты. Эти внутренние силовые факторы связаны с четырьмя простыми деформациями бруса: растяжением (сжатием), сдвигом, кручением и изгибом.
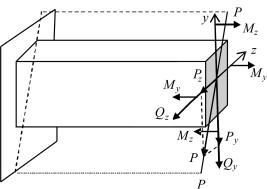
Косой изгиб – вид сложного сопротивления, при котором силовая плоскость Р-Р не совпадает ни с одной из главных плоскостей инерции бруса (рис. 1.1). При косом изгибе в поперечном сечении бруса возникают четыре внутренних усилия: Qz, Qy – поперечные силы; Мz, Мy – изгибающие моменты. Косой изгиб может рассматриваться как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях инерции.
Рис. 1.1
В общем случае действия нагрузок на брус для определения напряженного состояния используется принцип механики деформируемого твердого тела (в случае соблюдения закона
6
Гука между напряжением и деформацией) – принцип независимости действия сил, т.е. каждый из простых видов сопротивления, входящих в состав сложного, рассматривается независимо от остальных, а затем находится суперпозиция (сумма) полученных решений (для внутренних усилий, напряжений, деформаций и т.д.).
Общая методика решения задач на сложное сопротивление
1.Все заданные нагрузки проектируются на две главные плоскости инерции – плоскости, проходящие через продольную ось и одну из главных центральных осей инерции поперечного сечения.
2.В каждой плоскости строятся эпюры внутренних силовых факторов, сопоставление которых позволяет установить положение опасного сечения – сечения, в котором внутренние усилия максимальны по абсолютной величине.
3.В опасном сечении определяются наибольшие нормальные и касательные напряжения, находится положение нейтральной оси (линии) – это линия, во всех точках которой нормальные напряжения равны нулю, и устанавливается положение опасных, т.е. наиболее напряженных, точек при одновременном действии всех внутренних силовых факторов.
4.В опасной точке выясняется характер напряженного состояния и составляется условие прочности, на основании которого решается одна из трех типов задач (проверочная, проектировочная, определение несущей способности).
Если элемент бруса в опасной точке находится в линейном напряженном состоянии, то все напряжения одного вида суммируются алгебраически. Для обеспечения прочности бруса полученное таким образом наибольшее суммарное напряжение должно быть меньше допускаемого напряжения.
7
Если элемент бруса в опасной точке находится в сложном напряженном состоянии, то условие прочности составляется с применением одной из теорий предельного состояния.
Правило знаков для внутренних усилий: поперечные силы положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке; изгибающие моменты положительны, если вызывают растяжение в положительном квадранте координатной системы.
Основные формулы для расчетов
1. Общие результирующие внутренние усилия при сложном сопротивлении (см. рис. 1.1):
а) полная поперечная сила
Q = Qz2 + Qy2 ;
б) полный изгибающий момент
М= Мz2 + M y2 .
2.Нормальное напряжение при косом изгибе
σ = ± M y z ± M z y,
J y |
Jz |
где M y , M z – изгибающие моменты относительно осей y и z соответственно; J y , Jz – моменты инерции сечения; y, z – коор-
динаты точки, в которой определяется напряжение.
Mz, My, z, y подставляются с учетом знака (Mz > 0 и My > 0, если они вызывают растяжение в I четверти).
3. Условие прочности по нормальным напряжениям при косом изгибе
8
|
|
|
|
σmax |
= ± |
M y,max |
+ |
M z,max |
≤ [σ], |
|||
|
Wy |
|
||||||||||
|
|
|
|
|
|
|
|
|
Wz |
|||
где Wy |
= |
J y |
и Wz = |
|
Jz |
– моменты сопротивления попереч- |
||||||
|
|
|
||||||||||
z |
y |
|
|
|||||||||
|
|
max |
|
max |
|
|
|
|||||
ного сечения относительно осей y и z; [σ] – допускаемое нор-
мальное напряжение.
Знак каждого из слагаемых зависит только от знака опасной точки сечения, если главные центральные волокна направляем в сторону растянутых волокон.
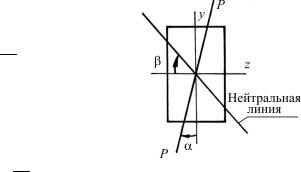
4. Уравнение нейтральной оси (линии) прикосомизгибе(рис. 1.2)
y = − Jz tgα z. J y
5. Уравнение наклона нейтраль- |
|
|
ной линии к оси Oz через угол β при |
|
|
косомизгибе |
|
|
tgβ = − Jz tgα. |
Рис. 1.2 |
|
J y |
||
|
Пример 1.1
Для заданного стального бруса (рис. 1.3) прямоугольного поперечного сечения подобрать размеры сечения с отношением сторон h/b = 4, если [σ] = 160 МПа.
Решение:
1. Определим внутренние силовые факторы. Мысленно разрежем брус по двум главным осям сечения. Построим эпюры изгибающих моментов (рис. 1.4, а, б).
9
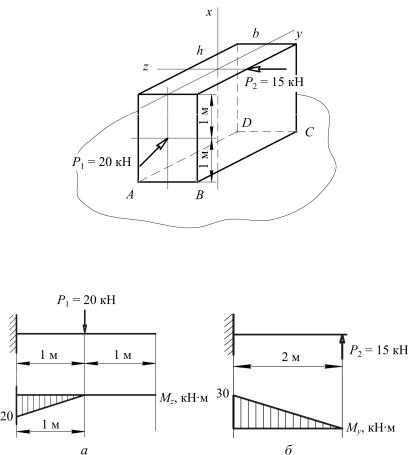
Рис. 1.3
Вертикальнаяплоскость(xOy) |
Горизонтальная плоскость(xOz) |
Рис. 1.4
2. Определим опасное сечение бруса – сечение, в котором внутренние силовые факторы максимальны по абсолютной величине.
Опасное сечение – заделка, в котором |Мz| = 20 кН·м;
Мy = 30 кН·м.
3. Определим опасные точки опасного сечения – точки, в которых напряжения максимальны по абсолютной величине.
10
