
Сопротивление материалов. Примеры решения типовых задач
.pdf
6. Результат перемножения двух эпюр по формуле Верещагина, если грузовая и единичная эпюры изгибающего момента являются линейными (рис. 3.1), условно называется «формулой трапеций»:
ωp yc = 6l (2 a c + 2 b d + a d + b c) .
Рис. 3.1
7. Результат перемножения двух эпюр по формуле Верещагина, если грузовая эпюра изгибающего момента в виде квадратной параболы, а единичная эпюра изгибающего момента в виде трапеции (рис. 3.2):
ωp yc = 6l (a c + b d + a d + 4 f h),
где |
f = |
a + b |
± e , |
e = |
ql |
2 |
– средняя ордината параболической |
|
|
|
|
||||||
2 |
8 |
|||||||
|
|
|
|
|
||||
эпюры от равномерно распределенной нагрузки q; h = c + d . 2
31

Рис. 3.2
Пример 3.1
Спомощью интеграла Мора определить прогиб в точке А
иугол поворота сечения в точке В балки, изображенной на
рис. 3.3, если жесткость балки EJ = 2 107 Н м2 .
Решение:
1.Вычертим схему нагружения балки с указанием всех числовых значений (см. рис. 3.3).
2.Определим реакции опор в балке на заданную нагрузку:
MC = RD 6 + M − q 2 3 + P 2 = 0,
RD = |
q 2 3 − M − P 2 |
|
= |
20 2 3 − 20 − 20 2 |
= 10 кН, |
|
|
|
6 |
||||
6 |
|
|
|
|||
M D = RC 6 + P 4 − q 2 3 − M = 0, |
|
|||||
RС = |
q 2 3 + M − P 4 |
= |
20 2 3 + 20 − 20 4 |
= 10 кН. |
||
|
6 |
|||||
6 |
|
|
|
|||
32

|
|
|
М = 20 кНм |
|||
RC |
|
|
|
|
RD |
|
C |
B |
q = 20 кН/м |
||||
Р= 20 кН |
|
А |
D |
|||
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|||
2 м |
|
2 м |
|
2 м |
||
х1 |
|
|
|
х3 |
||
х2
Рис. 3.3
Проверим правильность вычисления реакции опор:
M A = RD 2 + M + q 2 1− P 2 − RC 4 = 20 + 20 + 40 − 40 − 40 = 0.
Реакции найдены правильно.
3. Записываем уравнения изгибающих моментов для балки с заданной нагрузкой:
x1 (0; 2) : M p( x1 ) = RC x1 ,
x2 (2; 4) : M p( x2 ) = RC x2 + P(x2 − 2) − q(x22− 2)2 ,
x3 (0; 2) : M p( x3 ) = RD x3.
4. Составляем первую вспомогательную систему. Освобождаем балку от заданной нагрузки и в точку А прикладываем единичную безразмерную силу P = 1 (рис. 3.4).
Определяем реакции опор на действие этой силы:
|
M |
|
R′ |
6 |
|
|
|
|
4 |
|
0; |
R′ |
|
2 |
, |
|
|
− Р |
= |
= |
|||||||||||||
|
C = D |
|
|
|
D |
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
M |
R′ |
6 |
|
|
|
|
2 |
|
0; |
R′ |
|
1. |
|||
− Р |
= |
= |
||||||||||||||
|
|
D = C |
|
|
|
C |
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33
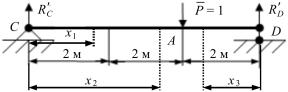
Рис. 3.4
Проверяем правильность вычислений реакции:
|
Y |
|
R′ |
|
|
|
R′ |
|
1 |
|
1 |
|
2 |
|
0. |
|
= |
− Р + |
= |
− |
+ |
= |
|||||||||||
|
C |
D |
3 |
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Реакции определены верно.
5. Записываем уравнения изгибающих моментов от действия на балку единичной силы:
|
|
|
|
1( x1 ) = |
R′ |
x , |
x (0; 2) : M |
||||||
1 |
|
|
|
C |
1 |
|
|
|
|
1( x2 ) = |
R′ |
x , |
|
x (2; 4) : M |
||||||
2 |
|
|
|
C |
2 |
|
|
|
1( x3 ) = |
R′ |
x . |
||
x (0; 2) : M |
||||||
3 |
|
|
|
D |
3 |
|
6. Определяем прогиб в точке А, составляя для каждого участка балки интегралы Мора и вычисляя их:
|
|
|
|
|
|
|
|
|
|
|
|
|
yA = |
|
1 |
M p M1dx = |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ i=1 l |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
{ |
2 |
R x R′ |
xdx |
|
4 |
[R x |
|
|
P(x |
|
2) |
|
q (x − |
2)2 ] |
R′ xdx |
|
|
|
||||||||||
|
|
= |
|
|
+ |
|
+ |
− |
− |
+ |
|
|
|||||||||||||||||||||
|
|
|
EJ |
|
C |
|
C |
|
|
|
|
C |
|
|
|
|
2 |
|
|
C |
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
R |
x R′ |
xdx} |
|
1 |
{ |
2 |
10x 1 xdx |
4 [10x |
|
20(x |
|
2) |
|
20 (x − |
2)2 |
] |
|
|||||||||||||||
+ |
= |
|
|
+ |
− |
− |
|
× |
|||||||||||||||||||||||||
|
D |
|
|
D |
|
|
EJ |
|
|
|
3 |
|
|
|
+ |
|
|
|
|
|
2 |
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
× |
1 |
|
|
|
|
2 |
|
2 |
xdx} = |
101,7 103 |
|
|
|
|
|
|
м = 0,5085 см. |
|
|
||||||||||||||
3 |
xdx + 10x |
3 |
|
|
2 10 |
7 |
= 0,5085 10−2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34

Положительный знак результата вычислений говорит о том, что балка в точке А прогибается по направлению дейст-
вия единичной силы P, т.е. вниз. Следовательно, прогиб балки
вточке А отрицательный и равен примерно 5,1 мм.
7.Составляем вторую вспомогательную систему. Освобождаем балку от заданной нагрузки и в точке B прикладываем
единичный безразмерный изгибающий момент М = 1 (рис. 3.5).
Рис. 3.5
Определяем реакции опор на действия этого момента:
|
M |
C = |
R′′ |
6 |
− |
|
|
|
|
= |
0; |
R′′ |
= |
1 |
, |
|||||||
M |
|
|||||||||||||||||||||
|
|
|
D |
|
|
|
|
|
|
|
D |
6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
M |
D = − |
R′′ 6 |
+ |
|
|
= |
0, |
R′′ |
= |
1. |
|||||||||||
M |
||||||||||||||||||||||
|
|
C |
|
|
|
|
|
C |
|
6 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Реакцию RC направляем вниз. Выполняем проверку:
|
M |
B = − |
R′′ 2 |
+ |
|
|
R′′ |
4 |
= − |
2 |
+ |
1 |
− |
4 |
= |
0. |
M |
||||||||||||||||
|
C |
|
|
− D |
|
6 |
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Реакции определены верно.
8. Записываем уравнения изгибающих моментов от действия на балку единичного момента:
x (0; 2) |
|
|
|
|
|
|
|
|
|
R′′ x , |
|||
: M |
2 |
|
|
|
|||||||||
1 |
|
|
|
|
|
( x1 ) = − C 1 |
|
|
|
||||
|
|
|
|
|
|
|
= − |
R′′ x |
|
|
|
||
x (2; 4) : M |
2( x2 ) |
M , |
|||||||||||
2 |
|
|
|
C 2 + |
|
|
|
||||||
|
|
|
( x3 ) = |
R′′ x . |
|
|
|
||||||
x (0; 2) : M |
2 |
|
|
|
|||||||||
3 |
|
|
|
|
|
|
D 3 |
|
|
|
|||
35

8. Составляем для каждого участка балки интегралы Мора и, вычисляяих, определяемуголповоротасечениябалкивточкеB:
|
|
|
|
|
|
θВ = |
1 M pM2dx = |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ i=1 l |
|
|
|
|
|
|
|
|
|
|||
= |
1 |
{2 RC x (−RC′′ x)dx + 4 [RC x + P(x − 2) − q |
(x − 2)2 |
] (−RC′′ |
|
|
|
||||||||||||
+ M |
)dx + |
||||||||||||||||||
EJ |
2 |
||||||||||||||||||
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ 2 RD x RD′′ xdx} = |
1 |
{2 10x (− |
1)xdx |
+ 4 [10x + 20(x − 2) − 20 |
(x − 2)2 |
]× |
|||||||||||||
EJ |
2 |
||||||||||||||||||
0 |
|
|
|
|
0 |
|
6 |
2 |
|
|
|
|
|
||||||
|
|
× (1− |
1 |
|
|
2 |
1 |
xdx} = |
35,6 103 |
10−3 рад. |
|
||||||||
|
|
6 |
x)dx + 10x |
6 |
7 |
= 1,78 |
|
||||||||||||
|
|
|
|
|
0 |
|
|
2 10 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положительный знак результата вычислений говорит о том, что поворот сечения балки в точке B происходит по направлению единичного изгибающего момента. Следовательно, поперечное сечениев этойточкебалкиповернетсяпочасовойстрелке.
Пример 3.2
Для рамы, изображенной на рис. 3.6, а, определить по способу Верещагина величины вертикального и горизонтального перемещения и угла поворота сечения свободного конца рамы, если жесткость стержней рамы ЕJ = 2·107 Н·м2.
Решение:
1.Вычертим расчетную схему рамы с указанием всех числовых значений (см. рис. 3.6, а).
2.Для рамы с заданной нагрузкой строим грузовую эпюру изгибающих моментов Мр, которая изображена на рис. 3.6, б.
3.Составляем первую вспомогательную систему. Освобождая раму от заданной нагрузки, прикладываем к свободному
концу вертикальную единичную силу Р1 = 1 (рис. 3.6, в) и строим единичную эпюру изгибающих моментовМ1 , которая изображена на рис. 3.6, г.
36
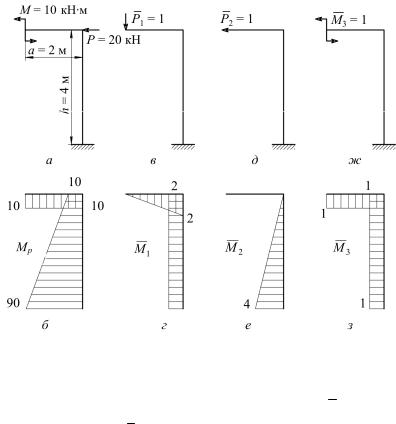
Рис. 3.6
4. Находим величину вертикального перемещения свободного конца рамы. Перемножим эпюры Мр и М1 , так как эпюра Мр и эпюра М1 линейные по участкам рамы, можно их перемножить по способу Верещагина:
|
|
|
|
yA = |
1 |
ωp |
yc |
= |
1 |
[ |
2 |
(2 10 2 +10 2) + |
|
|||
|
|
|
|
EJ |
|
6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
||||
|
|
|
|
+ |
4 (2 10 2 + 2 90 2 +10 2 + 90 2)] = |
|
||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
4 |
|
|
420 |
103 |
4, 2 105 |
= 2,1 10−2 |
= 2,1 см. |
||||
= |
|
( |
6 |
60 + |
6 |
600) = |
|
= |
|
2 107 |
||||||
EJ |
|
|
||||||||||||||
|
|
|
|
|
EJ |
|
|
|
||||||||
37

5. Составляем вторую вспомогательную систему. Освобождая раму от заданной нагрузки, прикладываем к свободному концу горизонтальную единичную силу Р2 = 1 (рис. 3.6, д) и строим
единичную эпюру изгибающих моментов М2 (рис. 3.6, е).
6. Находим величину горизонтального перемещения сво-
бодного конца рамы. |
|
|
|
|
2 , так как |
||||||
Перемножим эпюры Мр и М |
|||||||||||
эпюра Мр |
|
|
|
|
|
линейные по участкам рамы, можно их |
|||||
и эпюра М |
2 |
||||||||||
перемножить по способу Верещагина: |
|||||||||||
|
хA = |
1 |
ωp yc = |
1 |
4 (2 4 90 +10 4) = |
||||||
|
|
|
|||||||||
|
|
EJ |
|
EJ 6 |
|||||||
= |
4 760 103 |
15, 2 105 |
= 2,53 10−2 м = 2,53 см. |
||||||||
= |
3 2 107 |
||||||||||
|
6 EJ |
|
|
|
|
||||||
7. Составляем третью вспомогательную систему. Освобождая раму от заданной нагрузки, прикладываем к свободному концу безразмерный единичный изгибающий момент М3 = 1
(рис. 3.6, ж) и строим единичную эпюру изгибающих моментов
(рис. 3.6, з).
8. Находим величину угла поворота поперечного сечения свободного конца рамы. Перемножим эпюры Мр и М3 , при этом будем вычислять площади 1-го и 2-го участков эпюры Мр и умножать эти площади на ординаты эпюры М3 , взятые под центрами тяжести площадей эпюры Мр:
|
|
θA = |
1 |
ωp yc = |
1 |
(ω1p yc1 + ω2p yc2 ) = |
|||||||
|
|
EJ |
|
||||||||||
|
|
|
|
|
|
|
|
|
EJ |
|
|
||
= |
1 |
(10 |
2 1 |
+ |
(10 |
+ |
90) |
4 1) = |
220 103 |
= 0,011 рад. |
|||
EJ |
|
2 |
|
2 107 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
38

Задание 3.1
Определить с помощью интеграла Мора прогиб точек, указанных буквой А, и угол поворота сечений, указанных буквой В, для балок. Жесткость балок EJ = 2·107 Н·м2.
Содержание работы:
1.Для балки с заданной нагрузкой определить реакции опор и выполнить проверку правильности определения реакций.
2.Для каждого участка с заданной нагрузкой составить уравнения изгибающих моментов Мр.
3.Составить первую вспомогательную систему. Освободить балку от заданных нагрузок и приложить в точку А (в которой требуется определить вертикальное перемещение) верти-
кальную безразмерную силу P = 1 .
4.Для вспомогательной системы определить реакции опор
ивыполнить проверку правильности определения реакций.
5.Балку с единичной нагрузкой разбить на участки, идентичные участкам балки с заданной нагрузкой, и для каждого из
них составить уравнения изгибающих моментов M1 , соблюдая
идентичность в выборе начала координат для участков с единичной и заданной нагрузками.
6.Вычислить интегралы Мора в пределах каждого участка балки и, суммируя результаты вычислений, найти величину вертикального перемещения точки А.
7.Составить вторую вспомогательную систему. Освободить балку от заданных нагрузок и приложить в точку В (в которой требуется определить угол поворота сечения) единичный
безразмерный изгибающий момент M = 1.
8. Для балки, нагруженной только единичным изгибающим моментом, определить реакции опор, разбить балку на участки, идентичные участкам балки с заданной нагрузкой, и для
каждого из них составить уравнения изгибающих моментов M2 ,
соблюдая идентичность выбора начала координат для участков с единичными и заданными нагрузками.
39

Рис. 3.7
40
