
- •Аннотация
- •Введение
- •Термины и определения
- •Биометрические методы идентификации
- •Анатомия пальца человека
- •Общие сведения о преобразовании Габора
- •Обзор существующих методов генерации отпечатков пальцев
- •Обзор существующего программного обеспечения
- •Введение
- •Формализация алгоритма генерации искусственных биометрических образов
- •Математическая постановка задачи
- •Обоснование выбранного решения
- •Введение
- •Разработка общей структуры по
- •Выбор языка программирования
- •Выбор типа оп и формирование глобальных признаков
- •Построение поля направлений
- •Построение шаблона
- •Применение фильтра Габора
- •Обрезание изображения
- •Введение
- •Расчёт трудоёмкости проекта
- •4.2.2 Построение сетевого графика
- •4.2.3 Диаграмма Гантта
- •4.2.4 Анализ структуры затрат проекта
- •4.2.5 Затраты на выплату заработной платы
- •4.2.6 Отчисления на социальные нужды
- •4.2.7 Материальные затраты
- •4.2.8 Прочие затраты
- •4.2.9 Затраты на организацию рабочих мест
- •4.2.10 Накладные расходы
- •4.2.11 Суммарные затраты на реализацию программного проекта
- •Исследование рынка
- •4.3.1 Планирование цены и прогнозирование прибыли
- •4.3.2 Сервисное обслуживание
- •4.3.3 Отчисления на социальные нужды
- •Введение
- •Конституция Российской Федерации
- •Доктрина информационной безопасности Российской Федерации
- •Федеральный Закон «Об информации, информационных технологиях и о защите информации»
- •Федеральный Закон «о персональных данных»
- •Постановление Правительства Российской Федерации «Об утверждении требований к защите персональных данных при их обработке в информационных системах персональных данных»
- •Гражданский Кодекс Российской Федерации
- •Уголовный Кодекс Российской Федерации
Общие сведения о преобразовании Габора
Пусть
имеется функция
![]() ,
тогда преобразование Фурье для этой
функции выглядит следующим образом:
,
тогда преобразование Фурье для этой
функции выглядит следующим образом:
![]()
Преобразование
Фурье дает частотную информацию,
содержащуюся в сигнале, то есть показывает,
каково содержание каждой частоты в
сигнале. Интеграл берется от
![]() до
до![]() по всей временной оси. Время возникновения
конкретной частоты учитывается, так
как для преобразования Фурье её вклад
будет равнозначным вне зависимости от
её протяжения.
по всей временной оси. Время возникновения
конкретной частоты учитывается, так
как для преобразования Фурье её вклад
будет равнозначным вне зависимости от
её протяжения.
Из вышесказанного следует, что преобразование Фурье непригодно для анализа нестационарных сигналов. Исключением является случай, когда учитывается только частотная информация, а время существования спектральных составляющих не имеет значения.
Для исправления этих недостатков может быть использовано преобразование Габора. Пусть
 ,
,
где
![]() - фиксированный параметр.
- фиксированный параметр.
Функция
![]() используется в качестве так называемого
временного окна.
используется в качестве так называемого
временного окна.
Преобразованием Габора функции fявляется следующее выражение:
![]()
где b – параметр, используемый для сдвига окна.
Преобразование Габора локализирует преобразование Фурье вокруг точки t = b.
Алгоритм построения одномерного фильтра Габора
Для построения одномерного фильтра Габора применяется формула:
 ,
,
где
![]() - стандартное отклонениеГаусового
ядра, определяющее амплитуду функции;
- стандартное отклонениеГаусового
ядра, определяющее амплитуду функции;
![]() - частота колебаний.
- частота колебаний.
Чем
больше значение ![]() ,
тем более пологий вид примет функция,
и напротив, чем меньше значение, тем
более острый пик получится в результате
построения графика функции.
,
тем более пологий вид примет функция,
и напротив, чем меньше значение, тем
более острый пик получится в результате
построения графика функции.
Частота колебаний определяется как
![]() ,
,
где Т – период функции косинуса.

Рисунок 7. Функция Габора, представляющая собой композицию функции косинуса и экспоненты.
Пространственный фильтра Габора для двухмерных изображений
Формула функции Габора выглядит следующим образом:
![]() ,
,
где
![]() - комплексная синусоида, а
- комплексная синусоида, а![]() - огибающая Гаусса для двумерного
пространства. Остановимся более подробно
на этих составных частях фильтра Габора.
- огибающая Гаусса для двумерного
пространства. Остановимся более подробно
на этих составных частях фильтра Габора.
Комплексная синусоида
Комплексная синусоида определяется как
![]() ,
,
где
![]() и Р определяются как пространственная
частота и фаза синусоиды.
и Р определяются как пространственная
частота и фаза синусоиды.
Можно представить синусоиду как две действительные функции, расположенные в действительной и мнимой части комплексной функции.

Рисунок
8.
Действительная и мнимая часть комплексной
синусоиды с параметрами:
![]() ,
,![]() .
.
Действительная и мнимая части синусоиды имеют вид:

Параметры
![]() определяют частоту синусоиды в декартовых
координатах.
определяют частоту синусоиды в декартовых
координатах.
Огибающая Гаусса
Огибающая Гаусса имеет вид:
![]() ,
,
где
![]() - координаты пика функции,а
и b
скалярные параметры Гауссиана,
- координаты пика функции,а
и b
скалярные параметры Гауссиана,
![]() - индекс, обозначающий операцию вращения,
такой, что:
- индекс, обозначающий операцию вращения,
такой, что:
 .
.
Иллюстрация огибающей Гаусса представлена на рисунке 9.
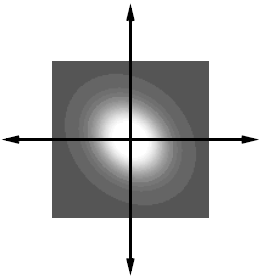
Рисунок
9.
Огибающая Гаусса при значениях параметров:
![]()
Комплексная функция Габора
Комплексная функция Габора определяется следующими 9 параметрами:
K- весовая величина огибающей Гаусса
(a,b)- весовые величины огибающей, распределенные по осям
 -
угол вращения огибающей Гаусса
-
угол вращения огибающей Гаусса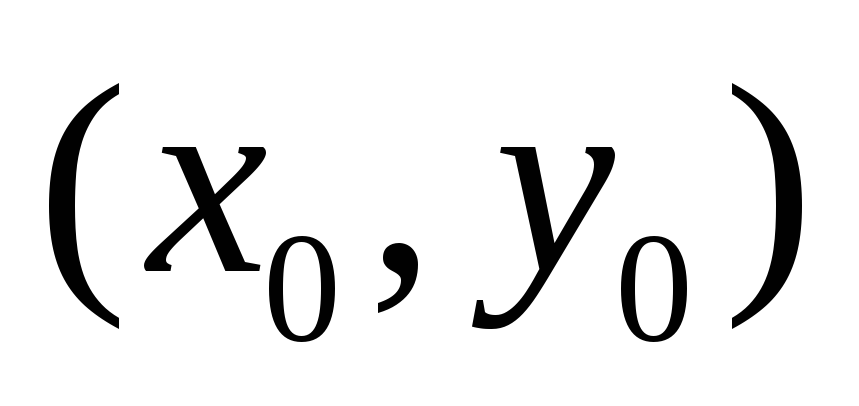 -
координаты пика огибающей Гаусса
-
координаты пика огибающей Гаусса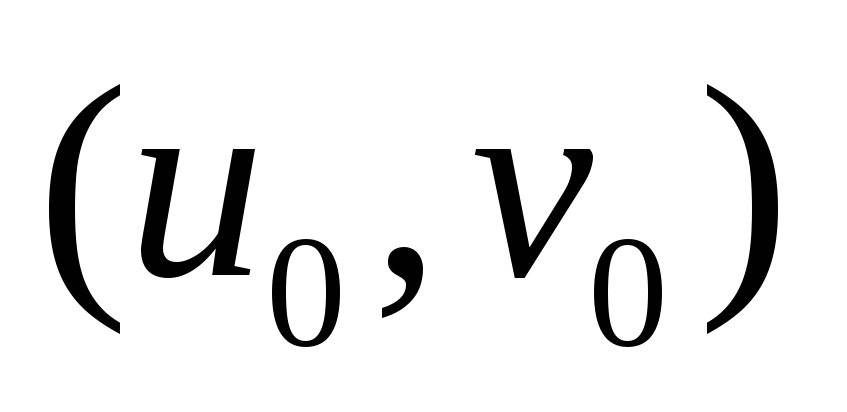 -
пространственные частоты комплексной
синусоиды
-
пространственные частоты комплексной
синусоидыР - фаза комплексной синусоиды
Каждая комплексная функция Габора состоит из двух частей, расположенных в действительной и мнимой части функции (Рисунок 10).

Рисунок 10. Действительная и мнимая часть комплексной функции Габора.
Таким образом, функция Габора имеет вид:
![]()
Алгоритм построения двумерного фильтра Габора
Для построения двумерного фильтра Габора применяется формула

где
![]() ,
,![]() ;
;![]() и
и![]() - стандартные отклонения Гауссова ядра
по осям соответственно, определяющая
растянутость фильтра по осям;
- стандартные отклонения Гауссова ядра
по осям соответственно, определяющая
растянутость фильтра по осям;![]() - частотная модуляция фильтра;
- частотная модуляция фильтра;![]() - пространственное направление фильтра,
определяющее ориентацию фильтра
относительно осей xиy.
- пространственное направление фильтра,
определяющее ориентацию фильтра
относительно осей xиy.

Рисунок
11. Графическое
представление фильтра Габора (визуализация
двухмерного фильтра Габора в трехмерном
пространстве и пример применения фильтра
с ориентацией
![]() ).
).
Применение фильтра Габора для двухмерных изображений
Фильтр настраивается на локальную ориентацию выступов, применяется к пикселям выступов и впадин изображения.

где
![]() ;
;![]() ;
;![]() - ориентация фильтра Габора,
- ориентация фильтра Габора,![]() - частота, а
- частота, а![]() и
и![]() - пространственные константы огибающей
Гаусса вдоль осейxиyсоответственно.
- пространственные константы огибающей
Гаусса вдоль осейxиyсоответственно.
Для использования Фильтра Габора нам необходимо знать значения следующих величин:
1) направление фильтра
2) частоту синусоидальной плоскостной волны
3)
![]() и
и![]() - среднеквадратичные отклонения огибающей
Габора
- среднеквадратичные отклонения огибающей
Габора
