Московский Государственный Технический Университет

имени Н.Э.Баумана

(МГТУ им. Н.Э. Баумана)

факультет «Инженерный Бизнес и Менеджмент»

кафедра ИБМ2

«Экономика и организация производства»

Дисциплина:

«Организационно-экономическое моделирование»

Домашнее задание:

«Оценивание функции спроса»

(Вариант 12)

Выполнила: студентка группы ИБМ5-71

Мухина Татьяна

Принял преподаватель:

Куликова Светлана Юрьевна

Москва, 2012 г.

Целью выполнения домашнего задания является определение наилучшей аппроксимации функции, которая даёт наиболее точное приближение функции спроса, то есть на основе чего следует делать вывод о назначении цены изделия.

Для достижения поставленной цели необходимо выполнить следующие задачи:

• упорядочить и проанализировать данные, полученные от респондентов;

• определить спрос на товар;

• построить выборочную функцию спроса;

• обработать данные с помощью метода наименьших квадратов;

• рассчитать прибыль при различных издержках;

• построить восстановленные функции спроса, используя линейную и степенную аппроксимации;

• на основе рассчитанного показателя качества эконометрической модели сделать вывод о том, какой способ аппроксимации позволяет наиболее точно проанализировать функцию проса.

В ходе выполнения домашнего задания был использован учебник «Эконометрика» А.И. Орлова, 4 издание.

В результате опроса получено 50 ответов на вопрос: «Какую максимальную цену вы готовы заплатить за подарок другу (подруге) на День Рождения?»

По данным опроса удалось выяснить, что цена, которую готовы заплатить респонденты колеблется от 500 до 5000 (руб.), данные представлены в табл.1.

Таблица 1

«Данные опроса»

№	Pi	№	Pi	№	Pi	№	Pi	№	Pi
1	1000	11	1500	21	500	31	4500	41	500
2	3500	12	2500	22	2000	32	1500	42	2000
3	1500	13	3000	23	4500	33	1500	43	2500
4	2000	14	500	24	1000	34	2500	44	3000
5	4000	15	2000	25	1500	35	2000	45	4000
6	3500	16	4500	26	5000	36	5000	46	1500
7	500	17	1000	27	4000	37	4500	47	5000
8	2500	18	3500	28	5000	38	500	48	500
9	1500	19	2500	29	2000	39	3000	49	1000
10	3000	20	5000	30	3000	40	1500	50	3500

Перейдём к анализу подученных данных, для этого упорядочим все значения по возрастанию и посчитаем сколько раз названа каждая цена.

Таким образом получилось, что 50 опрошенных потребителей назвали 10 конкретных максимально допустимых для них значений цены. Каждое из значений названо от 3 до 8 раз, как видно из табл. 2.

Таблица 2

«Оценивание функции спроса и расчет оптимальной цены»

№	Цена Pi	Ni	Спрос D(Pi)	Прибыль (Pi-120)*D(Pi)	Прибыль (Pi-1000)*D(Pi)	Прибыль (Pi-1500)*D(Pi)	Прибыль (Pi-2100)*D(Pi)	Прибыть (Pi-2700)*D(Pi)
1	500	6	50	19000	-25000	-50000	-80000	-110000
2	1000	4	44	38720	0	22000	-48400	-74800
3	1500	8	40	55200	20000	0	-24000	-48000
4	2000	6	32	60160	32000	16000	-3200	-22400
5	2500	5	26	61880	39000	26000	10400	-5200
6	3000	5	21	60480	42000	31500	18900	6300
7	3500	4	16	54080	40000	32000	22400	12800
8	4000	3	12	46560	36000	30000	22800	15600
9	4500	4	9	39420	31500	27000	21600	16200
10	5000	5	5	24400	20000	17500	14500	11500

На рис.1 представлена зависимость спроса от цены в соответствующих координатах.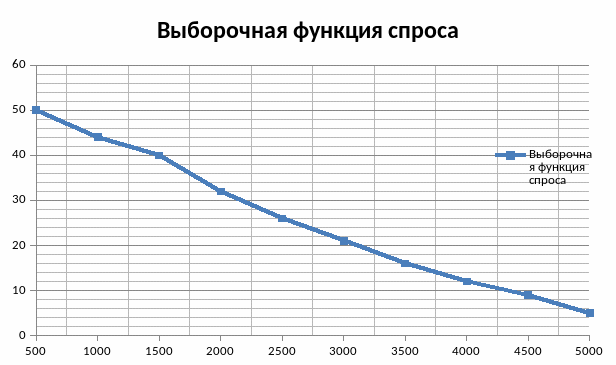

Рисунок 1: «Выборочная оценка функции спроса»

По данным графика видно, что при увеличении цены спрос падает практически в линейной зависимости. За минимальную цену подарок готовы купить все респонденты, а за максимальную лишь 5.

В столбцах 5 – 9 подсчитана прибыль по следующей формуле:

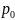( - )*D( ) , где - это издержки (т.е. оптовая цена)

Выбраны предполагаемые издержки: : 120 , 1000 , 1500 , 2100 , 2700.

Анализируя таблицу 2, видим, что при издержках 120 руб. максимум прибыли-61880 приходится на цену 2500 руб., что говорит о том, что товар купят 26 человек из 50-ти. Это 52% или около половины всех возможных покупателей.

При повышении издержек максимум прибыли достигается за счет продажи товаров меньшему количеству людей, но по более высокой цене:

= 1000 , max прибыли-42000 приходится на p = 3000

= 1500 , max прибыли-32000 приходится на p = 3500

= 2100 , max прибыли-22800 приходится на p = 4000

= 2700 , max прибыли-16200 приходится на p = 4500

Таким образом, необходимо стремиться к уменьшению издержек и ориентироваться на покупателя со средними возможностями, при этом будет достигнута максимальная прибыль.

Для сравнения возьмем издержки 1500 руб. при цене 2000 и издержки 2700 при цене 4500, что соответствует получение практически одинаковой прибыли в 16000 и 16200 руб. В первом случае товар будет продан 32 покупателям, во втором только – 9. То есть выгоднее пытаться уменьшать издержки и сохранять потребителей.

Функция спроса была исследована только при названных значениях цены, целесообразно восстановить её при всех возможных значениях цены, а затем использовать эту восстановленную зависимость для расчета оптимальной цены при различных значениях издержек. Восстановить зависимость можно с помощью метода наименьших квадратов.