
- •«Московский государственный технический университет имени н.Э. Баумана» (мгту им. Н.Э.Баумана)
- •Домашнее задание по дисциплине «Теория вероятностей и математическая статистика» Вариант № 15
- •1)Найти центр рассеивания случайного вектора (X, y).
- •3) Построить ковариационную и корреляционную матрицы.
- •Найти центр рассеивания случайного вектора (X, y).
- •Построить ковариационную и корреляционную матрицы.
- •Найти центр рассеивания случайного вектора (X, y).
- •Построить ковариационную и корреляционную матрицы.
Государственное образовательное учреждение
высшего профессионального образования
«Московский государственный технический университет имени н.Э. Баумана» (мгту им. Н.Э.Баумана)
________________________________________________________________________
Факультет
«Специальное машиностроение»

Домашнее задание по дисциплине «Теория вероятностей и математическая статистика» Вариант № 15
ИСПОЛНИТЕЛЬ
студент гр. СМ 10-71 Стрельченко Кирилл
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
Москва
Задача 1.
Закон распределения случайного вектора (X, Y) задан в табличном виде:
pij |
xi |
|||
0 |
2 |
5 |
||
yj |
0 |
1/9 |
1/9 |
1/9 |
2 |
0 |
1/6 |
1/6 |
|
5 |
0 |
0 |
1/3 |
|
Найти центр рассеивания случайного вектора (X, Y).
Вычислить условное математическое ожидание M[X/Y = 2] и дисперсию D[X/Y = 2].
Построить ковариационную и корреляционную матрицы.
Установить закон распределения случайных величин: S = X + Y и Z = XY.
1)Найти центр рассеивания случайного вектора (X, y).
Условия
нормировки
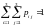 выполняется:
выполняется:
1/9+1/9+1/9+1/6+1/6+1/3=1/3+1/3+1/3=1.
Сложим вероятности по столбцам, получим закон распределения Х:
X |
0 |
2 |
5 |
рX |
1/9 |
1/9+1/6=5/18 |
1/9+1/6+1/3=11/18 |
Сложим вероятности по строкам, получим закон распределения Y:
Y |
0 |
2 |
5 |
рY |
3/9 |
2/6 |
1/3 |
Математическое
ожидание Х: M(X)=∑xi*pxi=0*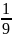 +2*
+2*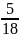 +5*
+5* =3,6111=
=3,6111=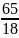
Математическое
ожидание Y:
M(X)=∑yj*pyj
=0*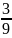 +2*
+2*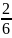 +5*
+5*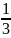 =2,333=
=2,333=
Центр
рассеивания случайного вектора (X, Y):
M(X,Y)=(M(X),M(Y))=(9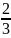 ,6
)
2)
Вычислить условное математическое
ожидание M[X/Y = 2]
и дисперсию D[X/Y = 2].
,6
)
2)
Вычислить условное математическое
ожидание M[X/Y = 2]
и дисперсию D[X/Y = 2].
Найдем закон распределения X при условии Y=2.
Условные
вероятности X:
p(X=xi/Y=2)=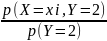
P(X=0/Y=2)=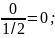
P(X=0/Y=2)=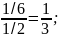
P(X=0/Y=2)=
X |
0 |
2 |
5 |
p(X/Y=3) |
0 |
1/2 |
1/2 |
M(X/Y=2)=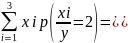 0*0+2*
+5*
=3,5
0*0+2*
+5*
=3,5
D(X/Y=2)=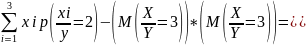 02*0+22*
02*0+22* 52*
=9
52*
=9
3) Построить ковариационную и корреляционную матрицы.
Найдем ковариацию X и Y.
K(X,Y)=K(Y,X)=M((X-M(X))(Y-M(Y))=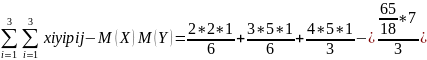 =
=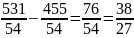 =1,41
=1,41
Найдем дисперсии X и Y по одномерным законам распределения.
D(X)=M((X-M(X)2)=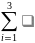 pxi-(M(X))2=02*
+22*
+52*
– (
)2=
pxi-(M(X))2=02*
+22*
+52*
– (
)2=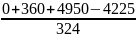 =
=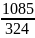 = 3,35
= 3,35
D(Y)=M((Y-M(Y))2=
pxi
– (M(Y))2
= 02*
+22*
+52*
– (
)2
=
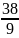 = 4,2
= 4,2
Ковариационная
матрица
 .
.
K
=(
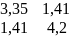 )
)
Коэффициент
корреляции rXY
= rYX
=
 =
=
 = 0,38
= 0,38
Корреляционная
матрица C
=(
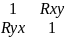 )
= (
)
= (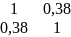 )
)
4) Установить закон распределения случайных величин: S = X + Y и Z = XY.
1)
Случайная величина X+Y
принимает значения
 с вероятностями
с вероятностями
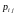 .
.
xi |
0 |
2 |
5 |
||||||
yj |
0 |
2 |
5 |
0 |
2 |
5 |
0 |
2 |
5 |
xi +y j |
0 |
2 |
5 |
2 |
3 |
7 |
5 |
7 |
10 |
p i j |
1/9 |
0 |
0 |
1/9 |
1/6 |
0 |
1/9 |
1/6 |
1/3 |
Объединяем повторяющиеся значения (если они есть), суммируя их вероятности. Значения, вероятности которых равны 0, исключаем.
Закон распределения X+Y:
X+Y |
0 |
2 |
5 |
3 |
7 |
10 |
pX+Y |
1/9 |
1/9 |
1/9 |
1/6 |
1/6 |
1/3 |
Контроль:
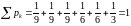 .
.
2)
Случайная величина XY
принимает значения
 с вероятностями
.
с вероятностями
.
xi |
0 |
3 |
5 |
||||||
yj |
0 |
3 |
4 |
0 |
3 |
4 |
0 |
3 |
4 |
xi y j |
0 |
0 |
0 |
0 |
9 |
12 |
0 |
15 |
20 |
p i j |
1/9 |
0 |
0 |
1/9 |
1/6 |
0 |
1/9 |
1/6 |
1/3 |
xi |
0 |
2 |
5 |
||||||
yj |
0 |
2 |
5 |
0 |
2 |
5 |
0 |
2 |
5 |
xi y j |
0 |
0 |
0 |
0 |
4 |
10 |
0 |
10 |
25 |
p i j |
1/9 |
0 |
0 |
1/9 |
1/6 |
0 |
1/9 |
1/6 |
1/3 |
Объединяем повторяющиеся значения (если они есть), суммируя их вероятности. Значения, вероятности которых равны 0, исключаем.
Закон распределения XY:
XY |
0 |
4 |
10 |
25 |
pX+Y |
1/3 |
1/6 |
1/6 |
1/3 |
Контроль:
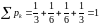 .
.
Задача 2.
Координаты X, Y случайного положения точки на плоскости имеют совместное равномерное распределение внутри области G = {(x, y) | –0 x 5, –5 y 2}.
