
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

функцией. Эта функция найдётся путём решения этого уравнения. Вторая функция найдётся с помощью одного из равенств системы.
Поступим так. Продифференцировав второе уравнение по переменной |
, |
|||||||||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В это равенство подставим |
|
|
из первого уравнения |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
системы, |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В последнее равенство |
|
подставим |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
значение |
, найденное из второго уравнения системы. Так как |
|
|
|
|
Итак, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
получили |
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с одной |
неизвестной |
|
функцией |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
. Это есть линейное однородное дифференциальное уравнение второго |
||||||||||||||||||||||||||||||||||||||||||
порядка с постоянными коэффициентами. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Находим решение |
|
|
|
|
|
|
|
|
полученного |
уравнения. |
Его характеристическое |
|||||||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет двукратный |
корень |
|
|
|
|
Тогда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
фундаментальную систему решений образуют функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
а общим решением является функция |
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Теперь |
найдём вторую функцию |
. Для |
этого надо |
найденную |
||||||||||||||||||||||||||||||||||||||
функцию |
|
|
и её |
производную |
|
|
|
|
|
|
подставить |
в |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
Проделав это, получим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Модуль 7. Числовые и функциональные ряды
Пример 1. Выписать первые четыре члена ряда |
, если его общий член |
||||
имеет вид |
|
|
|
|
|
|
|
|
|||
|
|
||||
Решение. Для получения членов ряда надо в формуле его общего члена 
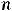 полагать
полагать 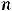

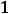
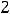
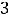
 . Тогда по заданной формуле получим
. Тогда по заданной формуле получим
Для дальнейшего рекомендуем обратить внимание, что множитель 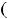

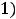
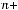
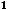 общего члена
общего члена 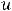 задаёт при данном
задаёт при данном 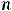 знак соответствующего члена ряда.
знак соответствующего члена ряда.
Ответ: 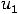

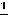
Пример 2. Записать в какой-нибудь форме общий член 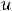 каждого из рядов
каждого из рядов
109

в предположении, что последующие члены имеют закономерность уже выписанных членов.
Решение. Выписанные члены первого ряда получаются из формулы 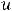

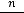 .
.
Если закономерность последующих членов сохраняется, то это и будет формула общего члена.
Знаки второго ряда получаются (плюс, минус) и это можно задать множителем 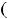

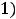
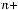
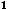 . Числители всех дробей равны единице, а знаменатели
. Числители всех дробей равны единице, а знаменатели
имеют вид 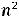 . Тогда можно считать, что
. Тогда можно считать, что 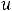


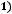 .
.
Знаки третьего ряда чередуются таким же образом. Числители дроби имеют номера натуральных чисел, а знаменатели получаются из выражения 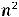
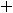
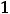 .
.
Можно предположить, что 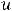


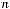 .
.
|
Ответы: |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 3. Из числовых рядов |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
выделить расходящиеся. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Решение. Если числовой ряд |
|
сходится, |
то |
|
|
|
|
Это |
|||||||||||
равенство есть необходимое условие |
сходимости ряда. |
Если оно не выполнено |
||||||||||||||||||
( |
|
|
, то ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Очевидно, что такими рядами являются ряды 2) и 4). Действительно, пределы общих членов этих рядов таковы: 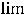
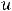

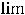
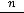

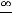

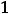
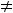
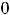
Очевидно, что для рядов 1) и 3) необходимое условие сходимости выполнено.
Однако это не означает, что они сходятся. Известно, что если |
, то |
|
ряд с общим членом |
может как сходиться, так и расходиться. Исследование |
|
этих рядов будет проведено в дальнейшем на основании признаков, дающих достаточные условия сходимости ряда.
Ответ: расходящимися являются ряды 2) и 4).
Пример 4. Исследовать на сходимость положительные ряды 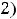
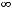
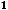
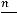

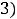
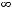
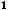
 по предельному признаку Даламбера.
по предельному признаку Даламбера.
110

Решение. Пусть ряд с общим членом |
строго положителен ( |
и |
|||
существует конечный предел |
|
|
Тогда при |
ряд сходится, при |
|
|
|
||||
ряд расходится, при |
ряд может как сходиться, так и расходиться |
||||
(признак ответа не даёт). |
|
|
|
|
|
Сформулированное утверждение называют предельным признаком
Даламбера. В случае, если |
|
|
|
|
|
не существует или |
|
(ситуация 3)) надо |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
применять какой-либо другой признак. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Для строго положительного ряда1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
и, следовательно, ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Для ряда 2) |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
, ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
В задании 3) |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Признак ответа не даёт. Далее этот ряд будет исследован |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
с помощью другого признака.
Ответы: 1) сходится; 2) расходится; 3) признак ответа не даёт.
Пример |
|
5. Исследовать |
на сходимость положительные ряды |
||||||||
|
|
|
|
|
|
|
|
|
|
по предельному признаку Коши. |
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
Пусть для положительного ряда |
существует конечный |
|||||||||
предел |
|
|
|
|
|
Тогда при |
|
ряд сходится, при |
ряд расходится, |
||
|
|
|
|
|
|
||||||
при |
|
ряд может как сходиться, так и расходиться. |
|
||||||||
Этот признак называют предельным признаком Коши или радикальным
признаком. |
|
|
|
|
|
|
|
||
В случае 1) |
|
|
|
|
|
. Следовательно, этот ряд |
|||
|
|
|
|
|
|||||
|
|
||||||||
сходится. |
|
|
|
|
|
|
|
||
Очевидно, что для второго ряда |
|
|
Данный числовой ряд |
||||||
|
|||||||||
расходится. Читатель легко установит, что у этого ряда |
. |
||||||||
Для ряда 3) |
|
|
. Признак ответа не даёт. |
|
|||||
|
|
||||||||
Ответы: 1) сходится, 2) расходится, 3) признак ответа не даёт.
111
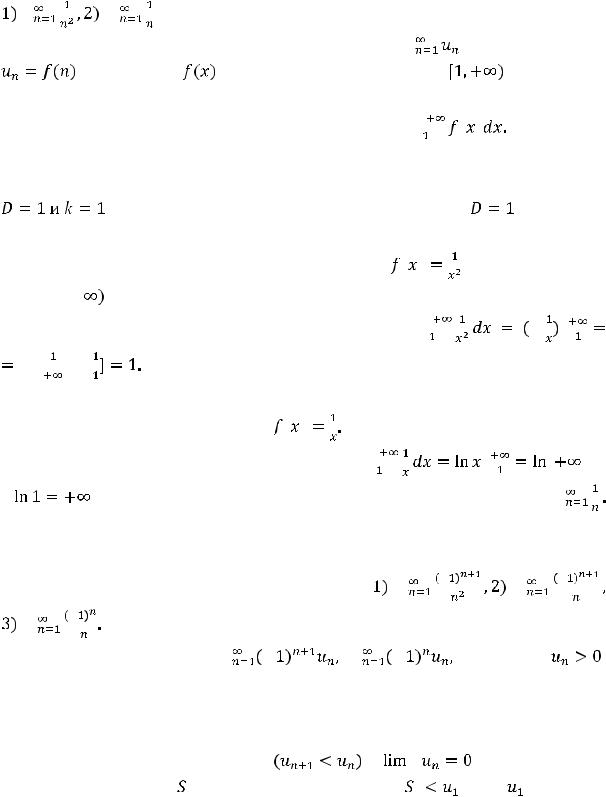
Пример |
6. Исследовать на сходимость положительные ряды |
||||||
|
|
|
|
|
по интегральному признаку. |
|
|
|
|
|
|
|
|||
Решение. |
Пусть члены |
положительного ряда |
не возрастают и |
||||
|
|
, где функция |
, определённая на промежутке |
, непрерывна, |
|||
неотрицательна и не возрастает. Тогда для сходимости такого ряда необходимо
и достаточно, чтобы сходился несобственный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Заметим, |
|
что ни признак Даламбера, ни признак Коши, рассмотренные ранее, |
|||||||||||||||||||||||||||||||||||||
не решают вопроса о |
сходимости |
этих |
рядов, так |
как в обоих случаях |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(читателю рекомендуем проверить это; |
что |
у ряда |
1), |
||||||||||||||||||||||||||
проверено в примере 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Для первого ряда в качестве функции возьмём |
|
|
|
|
. Очевидно, что на |
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
луче [1, + |
|
она удовлетворяет всем условиям сформированного признака. |
|||||||||||||||||||||||||||||||||||||||
Вычислим соответствующий несобственный интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Так как несобственный интеграл сходится, то сходится и ряд 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
В случае второго ряда полагаем |
|
|
Эта функция также удовлетворяет |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
условиям интегрального признака. |
Так |
как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(несобственный интеграл расходится), то расходится и ряд |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Напомним читателю, что этот ряд называют гармоническим. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
Ответы: 1) сходится; 2) расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Пример 7. Исследовать на сходимость ряды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ряды |
вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
все |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
называются знакочередующимися. Для таких рядов Лейбницем установлен
очень простой достаточный признак их сходимости. |
|
|
|||
Теорема |
Лейбница |
формулируется |
так: если |
модули |
членов |
знакочередующегося ряда убывают |
и |
, то ряд сходится; |
|||
при этом для |
суммы |
справедливо неравенство |
, где |
– модуль |
|
первого члена соответствующего ряда. |
|
|
|
||
112

Рассматриваемые ряды в более подробной записи таковы:
Очевидно, что для них выполняются условия теоремы Лейбница.
Следовательно, все ряды являются сходящимися. |
|
||||
Сумма |
первых двух рядов |
удовлетворяет неравенству |
, а |
||
третьего – неравенству |
|
|
. |
|
|
|
|
||||
Исследуем эти ряды на абсолютную сходимость. Знакочередующиеся ряды являются частным случаем знакопеременных рядов. Под последними понимаются ряды, содержащие бесконечное количество как положительных, так и отрицательных членов, расположенных в совершенно произвольном порядке.
Знакопеременный ряд |
называется абсолютно сходящимся, если он |
сходится вместе с рядом |
, составленным из абсолютных величин его |
членов. |
|
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а положительный ряд из модулей его ленов расходится.
Ряд 1) есть абсолютно сходящийся ряд, поскольку он сходится сам (это только что установлено по признаку Лейбница) и сходится ряд 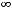
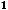
 (это установлено в примере 6).
(это установлено в примере 6).
Ряды 2) и 3) сходятся условно. Действительно, только что установлена их сходимость на основании признака Лейбница; соответствующие же им
положительные ряды |
|
и |
|
|
расходятся. Расходимость первого из них |
|
|
|
|||
|
|
(гармонического ряда) установлена в примере 6. Расходимость второго доказывается аналогично с помощью интегрального признака. В качестве 
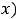 надо взять функцию
надо взять функцию 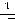 . Соответствующий несобственный интеграл рассмотрен
. Соответствующий несобственный интеграл рассмотрен
в примере 7 модуля 5.
Ответы: 1) сходится абсолютно; 2) и 3) – ряды сходятся условно.
Пример 8. Исследовать на сходимость знакочередующийся ряд
Решение. Чтобы не проверять выполнение условий теоремы Лейбница, применим теорему Коши, которая утверждает следующее: из сходимости
113

положительного ряда |
следует сходимость исходного знакопеременного |
|
ряда |
. |
|
Согласно этой теореме нужно исследовать положительный ряд с членами
|
|
|
. Применим радикальный |
признак |
Коши. Так как |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
то |
соответствующий |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
положительный ряд сходится. Согласно теореме Коши исходный ряд также сходится.
Таким образом, исходный ряд является абсолютно сходящимся. Ответ: сходится абсолютно.
Пример 9. Пользуясь определением суммы ряда, найти суммы рядов
Решение. Сумма первых 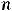 членов ряда называется n-й частичной суммой
членов ряда называется n-й частичной суммой
ряда и обозначается |
Если существует конечный предел |
последовательности |
частичных сумм ряда, то этот предел (число |
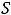 ) называется суммой ряда. Применим это определение для нахождения сумм рассмотренных рядов.
) называется суммой ряда. Применим это определение для нахождения сумм рассмотренных рядов.
Так как общий член первого ряда представим в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. ряд сходится и его сумма |
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Второй ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составлен из членов |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
бесконечной убывающей геометрической прогрессии |
|
|
|
|
|
|
с |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
первым членом |
|
|
|
и знаменателем прогрессии |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Известно, что сумма первых 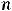 членов геометрической прогрессии при
членов геометрической прогрессии при 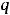
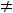
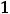
находится по формуле |
|
|
|
|
. Тогда для данного ряда |
|
|
|
|
||
|
|
|
|
|
|
Очевидно, что 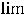
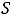

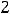 , т.е.
, т.е. 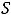

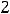

Ответы: 1) 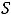

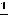

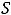

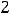

Пример 10. Представить в виде обыкновенной дроби следующие бесконечные десятичные периодические дроби: 1) 0,(2), 2) 0,(25), 3) 0,0(35).
114

Решение. Первое число 0,(2)=0,22… можно записать в виде геометрического
ряда |
|
|
|
|
|
с первым членом |
|
и знаменателем |
|
|
. |
||||||||||
|
|
|
|
|
|||||||||||||||||
Сумма этого ряда равна числу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь |
была применена формула |
|
|
|
нахождения |
суммы |
|||||||||||||||
|
|
|
|
||||||||||||||||||
сходящегося геометрического ряда.
Второе число 0,(25)=0,252 5… запишется в виде геометрического ряда 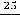
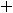
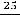
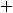
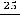
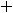
 с
с 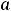

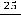 и
и 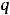

 . По той же формуле получаем, что
. По той же формуле получаем, что

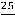 .
.
Третье число 0,0(35)=0,035 35… запишется в виде геометрического ряда
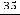
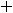
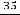
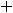
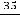
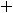
 , у которого
, у которого 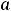

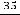 и
и 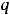

 . Тогда
. Тогда 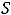

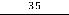

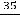 .
.
Ответы: 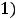
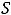

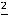

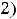
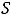

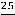

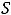

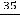

Пример 11. Вычислить приближённо сумму ряда 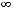
 с точностью
с точностью
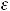

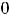
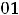 .
.
Решение. Данный ряд 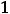

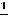

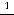
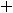
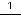

 является знакочередующимся.
является знакочередующимся.
Он сходится, так как выполняются условия теоремы Лейбница. Любой остаток также будет знакочередующимся рядом лейбницевского типа, при этом сумма 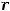 остатка после -го члена будет удовлетворять неравенству
остатка после -го члена будет удовлетворять неравенству 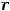
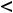
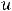
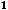

В данном примере 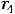
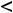

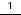
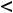
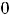
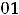 . Тогда для вычисления суммы ряда с указанной точностью
. Тогда для вычисления суммы ряда с указанной точностью 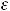

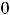
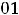 достаточно вычислить
достаточно вычислить 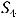 . Так как
. Так как 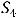

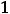

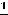
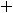
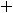
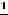

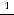

 , то
, то 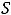
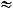
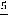 с точностью до 0,01.
с точностью до 0,01.
Ответ: 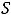
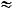
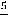 с точностью до 0,01.
с точностью до 0,01.
Пример 12. Найти области сходимости следующих степенных рядов:
Решение. Функциональные ряды вида

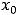
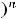 , где
, где 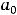
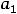
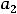

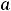
 есть постоянные действительные числа, называются степенными рядами. Обратим внимание на то, что в сокращённой записи этих рядов нумерация их членов начинается с нуля. Числа
есть постоянные действительные числа, называются степенными рядами. Обратим внимание на то, что в сокращённой записи этих рядов нумерация их членов начинается с нуля. Числа 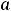
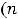

115

|
называются коэффициентами ряда. Если коэффициент |
|
задан |
|||||
формулой, |
не имеющей смысла при |
, то |
считают |
|
(обратите |
|||
внимание на записи данных рядов). |
|
|
|
|
|
|
|
|
Первый ряд расположен по целым неотрицательным степеням ( |
) |
|||||||
переменной |
, а второй – по степеням двучлена |
|
|
, где |
– |
некоторое |
||
|
|
|||||||
постоянное число, называемое центром ряда. Ясно, что первый ряд является частным случаем второго, поскольку получается из него при 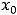

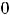

Множество тех значений 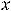 , для которых степенной ряд сходится, называют его областью сходимости. Из известной теоремы Абеля следует, что областью сходимости степенного ряда будет некоторый промежуток, который иногда может выродиться в одну точку.
, для которых степенной ряд сходится, называют его областью сходимости. Из известной теоремы Абеля следует, что областью сходимости степенного ряда будет некоторый промежуток, который иногда может выродиться в одну точку.
Для определения области сходимости любого |
из рядов можно применять |
предельные признаки Даламбера и Коши |
к положительным рядам |
соответственно с членами 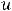
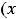
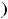

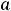
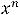
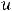
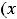
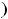

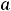
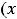

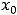
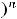 .
.
Обычно же области сходимости находятся с помощью числа 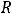 , называемого радиусом сходимости степенного ряда. Для нахождения
, называемого радиусом сходимости степенного ряда. Для нахождения 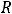 можно применять формулы
можно применять формулы 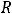

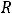

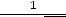 вытекающие из упомянутых признаков
вытекающие из упомянутых признаков
Даламбера и Коши. Обратим внимание на то, что в этих формулах участвуют не члены ряда, а его коэффициенты.
Если |
|
|
|
или |
|
|
, то |
считают |
тогда |
|||
|
|
|
||||||||||
степенной ряд сходится на всей числовой оси |
|
|
. Если |
|
|
|||||||
|
|
|
|
|||||||||
или |
|
|
|
то |
; тогда первый степенной ряд сходится только в |
|||||||
|
|
|
||||||||||
точке |
, а второй – в точке |
(это есть вырожденные случаи). |
|
|||||||||
Таким образом, можно считать, что радиус сходимости удовлетворяет
неравенствам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если |
есть конечное число, то первый ряд сходится абсолютно при |
|||||||||||||||
|
|
, т.е. на интервале |
|
, и расходится при |
. Надо будет ещё |
|||||||||||
|
||||||||||||||||
исследовать его на сходимость в точках |
|
|
|
|
на концах интервала. |
|||||||||||
|
||||||||||||||||
Таким образом, при |
|
возможны следующие промежутки сходимости |
||||||||||||||
первого степенного ряда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При таком |
второй степенной ряд будет абсолютно сходиться на интервале |
|||||||||||||||
|
|
|
Его сходимость на концах этого интервала надо будет |
|||||||||||||
|
|
|
||||||||||||||
проверять. Отметим, что при решении конкретных |
примеров можно ввести |
|||||||||||||||
|
|
|
|
|
|
116 |
|
|
|
|
|
|
||||

замену переменной |
|
|
|
|
|
и сначала устанавливать промежуток сходимости |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
относительно переменной по аналогии с первым степенным рядом. |
|
|
|
|
||||||||||||||||||||
Приступим к исследованию заданных степенных рядов. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
У первого ряда |
|
|
|
|
тогда |
|
так что |
. |
||||||||||||||||
Область сходимости |
степенного ряда состоит из одной |
точки |
, т.е. |
есть |
||||||||||||||||||||
множество |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
задании |
2) |
|
|
|
|
|
тогда |
|
|
|
|
|
и, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
следовательно, |
|
. Этот ряд сходится абсолютно на всей числовой оси. |
|
|||||||||||||||||||||
В |
примере |
|
3) |
|
|
|
|
тогда |
|
|
|
|
, т.е. |
. |
Ряд |
|||||||||
|
|
|
|
|
|
|
||||||||||||||||||
абсолютно сходится на интервале (-1,1). Надо проверить его сходимость на концах этого интервала.
|
При |
|
получим числовой знакочередующийся ряд |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
удовлетворяющий условиям теоремы Лейбница. Такой ряд сходится |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
(только условно). |
|
|
|
|
|
|
|
|||||||||||||||||
|
При |
|
получим ряд |
|
|
|
|
|
|
|
|
|
называемый |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
гармоническим. Уже было установлено, что он расходится.
Итак, ряд сходится на полуотрезке [-1, 1), при этом на интервале (-1,1)
сходится абсолютно. |
|
|
В задании 4) |
, тогда |
, т.е. |
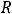

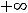 . Ряд сходится абсолютно на всей числовой оси.
. Ряд сходится абсолютно на всей числовой оси.
Теперь исследуем ряд 5), члены которого расположены по степеням двучлена
|
|
|
. |
Введём |
замену |
переменной |
|
|
|
|
|
Относительно переменной |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим степенной ряд первого типа, т.е. |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Так как |
|
|
|
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
следовательно, |
|
|
|
. Ряд сходится абсолютно для |
|
|
|
|
|
|
|
|
Исследуем точки |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
При |
|
|
|
|
получим числовой ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
, который сходится, так как отличается только знаком от сходящегося |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
ряда |
|
|
(сходимость последнего установлена в примере 6). При |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получаем знакочередующийся числовой ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
117 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

который сходится, т.к. удовлетворяет условиям теоремы Лейбница (см. пример 7); при этом сходится абсолютно.
Итак, |
ряд |
|
|
|
сходится абсолютно на отрезке [-1, 1], т.е. при всех |
||||||||
|
|||||||||||||
, удовлетворяющих неравенства |
|
|
. Тогда ряд 5) абсолютно сходится |
||||||||||
|
|||||||||||||
для всех |
, |
удовлетворяющих неравенствам |
|
|
|
или |
, т.е. |
||||||
|
|
|
|||||||||||
на отрезке [4, 6]. |
|
|
|
|
|
|
|
|
|||||
Ответы: |
1){0}; 2) |
сходится абсолютно на (- |
; 3) |
сходится на |
|||||||||
полуотрезке [-1, 1), при этом на интервале (-1, 1) сходится абсолютно; 4)
абсолютно сходится на (- |
; 5) сходится абсолютно на отрезке [4, 6]. |
||||||||||||||
Пример 13. Требуется разложить: 1) функцию |
|
|
|
|
|
|
|
в |
|||||||
|
|
|
|
||||||||||||
ряд Тейлора с центром в точке |
; 2) функцию |
|
|
в ряд Маклорена. |
|||||||||||
Решение. Если |
функция |
бесконечно дифференцируема в некоторой |
|||||||||||||
окрестности точки |
, то ряд |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
называется её рядом Тейлора с центром в точке |
||||||||||
|
|
|
|
|
|||||||||||
Коэффициенты ряда называются коэффициентами Тейлора. Ясно, что ряд
является степенным рядом по степеням двучлена |
|
|
Тогда он имеет область |
|||||||
|
||||||||||
сходимости, определяемую радиусом сходимости |
|
При |
определённых |
|||||||
условиях он своей суммой |
имеет функцию |
|
|
, по которой |
||||||
образован. |
|
|
|
|
|
|
|
|
|
|
Частным случаем |
является степенной ряд |
по целым |
||||||||
неотрицательным степеням |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
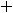
 , составленный по бесконечно дифференцируемой функции в окрестности нуля и называемый рядом Маклорена этой функции независимо от того, в какой
, составленный по бесконечно дифференцируемой функции в окрестности нуля и называемый рядом Маклорена этой функции независимо от того, в какой
области этот ряд сходится и является ли |
|
его суммой. |
|
|
||||||||||||
Найдём коэффициенты Тейлора первой |
заданной функции. Так как |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
все |
||
|
|
|
|
|
|
|
|
|
|
|||||||
производные высшего порядка равны нулю, то |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Все производные высшего порядка в точке |
|
|
||||||
также равны нулю; кроме того, |
|
|
|
|
|
|
|
|||||||||
Подставляя |
|
|
и значения найденных коэффициентов в выражение для |
|||||||||||||
ряда Тейлора |
функции 1), получим |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
. Ряд стоящий справа в этом равенстве, |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
представляет собой многочлен четвёртой степени по степеням двучлена |
|
. |
||||||||||||||
|
||||||||||||||||
|
|
|
|
|
118 |
|
|
|
|
|
|
|
||||

Очевидно, что он сходится на всей числовой оси и своей суммой имеет заданный
многочлен |
|
|
|
|
|
, только иначе записанный. |
|
|
||||
|
|
|
|
|
|
|
||||||
Теперь получим |
ряд Маклорена второй функции |
Для |
любого |
|||||||||
натурального числа |
|
справедливо равенство |
. Тогда |
|
||||||||
и при любом |
. |
|
|
|
|
|||||||
Подставляя найденные числа в |
выражение для ряда Маклорена, |
получим |
||||||||||
|
|
|
|
|
|
. |
Степенной |
ряд, стоящий |
справа |
в этом |
||
|
|
|
|
|
||||||||
равенстве, исследован в задании 4) примера 12; там установлено, что он абсолютно сходится на всей числовой оси. Можно показать, что его суммой является функция 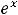 .
.
|
Отметим, |
|
что при |
имеем равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
которое позволяет вычислить приближённо значение числа Эйлера |
с любой |
||||||||||||||||||||||||||||||||||||||||||||||||||||
точностью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Ответы: |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 14. Найти член ряда Маклорена функции |
|
|
|
|
|
|
, содержащий |
|||||||||||||||||||||||||||||||||||||||||||||
степень . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение. Легко установить, что |
|
|
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
то из вида ряда Маклорена имеем, что этим членом будет |
|
|
|
или |
|
|
|
|
|
Читатель |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
может помнить, что разложение функции |
|
|
|
в ряд Маклорена имеет вид |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, отсюда сразу получаем тот же ответ. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Ответ: |
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Пример 15. Разложить в ряд Фурье функцию |
|
|
|
на отрезке [- |
. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. |
|
Рядом |
|
|
Фурье |
определённой |
и |
|
|
интегрируемой |
|
|
на |
отрезке |
||||||||||||||||||||||||||||||||||||||
[- |
|
|
|
функции |
называется тригонометрический ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
коэффициенты |
|
которого определяются |
равенствами |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
Найденные |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
по этим формулам числа называются коэффициентами Фурье функции |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Выясним вид ряда Фурье для нечётной и чётной функций. Для этого |
||||||||||||||||||||||||||||||||||||||||||||||||||||
воспользуемся фактически очевидными утверждениями: 1) если |
|
|
|
нечётна на |
|||||||||||||||||||||||||||||||||||||||||||||||||
отрезке [- |
|
, то |
|
|
|
|
|
|
2) если |
чётна на [- |
|
|
, то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
119 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
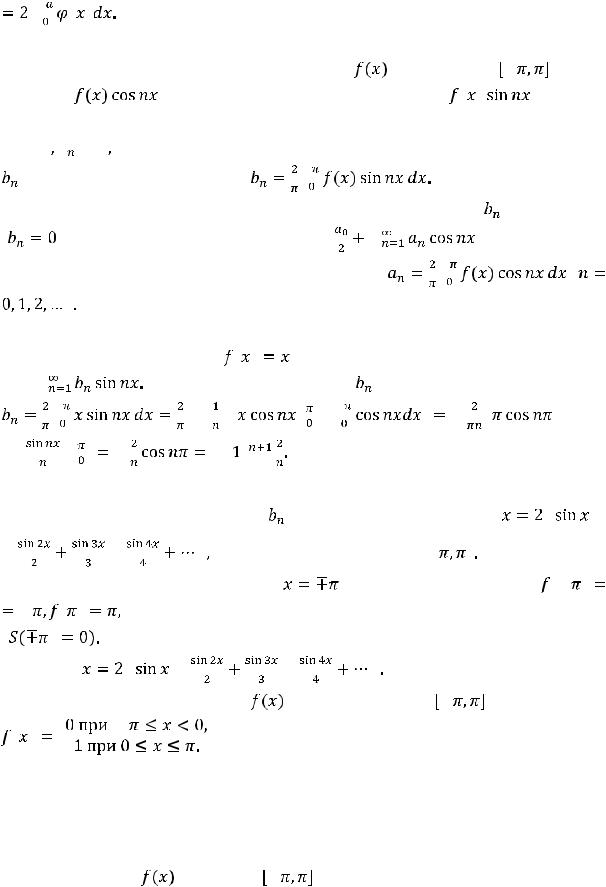
Они позволяют сделать вывод о значениях коэффициентов
Фурье. |
|
|
|
|
|
Пусть разлагаемая в ряд Фурье функция |
нечётная на |
|
. |
Тогда |
|
|
|||||
функция |
также нечётная на этом отрезке, а |
|
– |
чётная |
|
(воспользовались чётностью косинуса и нечётностью синуса). Следовательно, 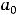

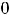
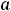

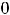 а ряд Фурье содержит только синусы. При этом коэффициенты
а ряд Фурье содержит только синусы. При этом коэффициенты
|
|
|
можно вычислять по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
Очевидно, что для |
чётной функции |
все |
коэффициенты |
равны нулю |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
|
|
|
|
) и |
её |
|
|
|
ряд |
Фурье примет |
|
вид |
|
|
|
|
, |
|
при этом |
все |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
коэффициенты |
|
|
|
|
можно |
|
|
|
найти |
по |
|
|
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Вид ряда чётной функции позволяет говорить, что он состоит из |
||||||||||||||||||||||||||||||||||||||||||||||||||||
косинусов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Так как заданная функция |
|
|
|
|
|
|
является нечётной, то её ряд Фурье имеет |
|||||||||||||||||||||||||||||||||||||||||||||||||||
вид |
|
|
|
|
|
|
|
|
|
Вычислим коэффициенты |
по преобразованной формуле |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
|
|
вычислении интеграла применены |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
формула интегрирования по частям и формула Ньютона-Лейбница. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
После подстановки найденных |
в ряд получаем равенство |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
справедливое на интеграле |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Отметим, что это |
равенство |
при |
|
|
|
|
|
|
|
неверно. Действительно, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а из самого ряда видно, что его сумма в этих точках равна нулю |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Ответ: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
|
|
|
|
|
|
|
на |
|
|
|
|
отрезке |
|
|
|
|
|
имеет |
вид |
||||||||||||||||||||||||||||
|
|
|
Пример |
16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется найти значение 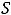
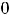
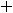
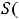
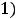 , где
, где 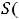
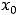
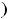 есть значение суммы ряда Фурье этой функции в точке
есть значение суммы ряда Фурье этой функции в точке 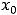

Решение. Воспользуемся теоремой Дирихле, дающей достаточные условия сходимости ряда Фурье, порождённого заданной функцией.
Пусть функция |
на отрезке |
|
удовлетворяет следующим условиям: |
|
|||
|
|
120 |
|
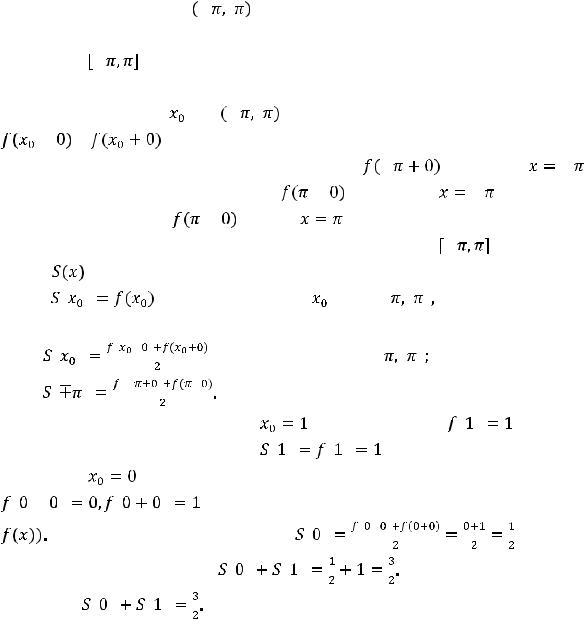
имеет |
на |
интервале |
|
|
|
|
|
|
|
|
|
разве |
лишь конечное |
число точек разрыва |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
первого рода; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отрезок |
|
|
|
|
|
|
можно разбить на конечное число интервалов, на каждом из |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
которых функция монотонна (либо неубывающая, либо не возрастающая); |
|||||||||||||||||||||||||||||||||||||||||||||||||
в точках разрыва |
|
из |
|
|
имеет конечные односторонние пределы |
||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
и |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
имеет |
конечный правосторонний |
предел |
|
|
|
|
|
|
|
в |
|
точке |
|
|
и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
конечный |
левосторонний |
|
|
|
предел |
|
|
|
|
|
в точке |
|
|
|
|
|
|
|
и |
конечный |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
левосторонний предел |
|
|
|
|
|
|
|
|
|
в точке |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Тогда ряд Фурье этой функции сходится на отрезке |
|
|
|
|
|
|
. При этом его |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
сумма |
удовлетворяет равенствам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
а) |
|
|
|
|
|
|
|
в |
каждой точке |
|
|
|
из |
|
|
|
|
|
|
в |
которой |
функция |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
непрерывна; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в точках разрыва из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Заданная |
функция |
в |
точке |
|
непрерывна и |
|
|
|
. |
Тогда по |
|||||||||||||||||||||||||||||||||||||||
утверждению а) теоремы Дирихле |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
В точке |
|
|
|
|
|
функция имеет разрыв первого рода. При этом очевидно, что |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рекомендуем построить график заданной функции |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Тогда по утверждению б) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Окончательно имеем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
121
