
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

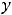

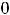 ; 10) односторонние горизонтальные асимптоты
; 10) односторонние горизонтальные асимптоты 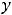


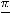
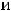
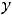

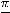 ; 11)
; 11)
двусторонняя горизонтальная асимптота 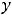

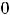 ; 12) левосторонняя наклонная асимптота
; 12) левосторонняя наклонная асимптота 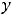


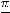
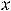

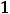 и правосторонняя наклонная асимптота
и правосторонняя наклонная асимптота 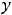

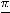
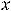

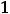 ; 13)
; 13)
параллельные наклонные асимптоты 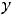

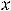

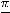 и
и 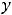

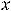
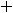
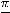 ; 14) вертикальная асимптота
; 14) вертикальная асимптота 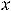

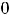 и горизонтальная асимптота
и горизонтальная асимптота 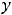

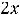

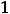 .
.
Модуль 3. Производная и дифференциал
Пример 1. По определению производной найти производные следующих функций:
1) |
|
|
|
, |
|
|
|
|
|
|
2) |
|
|
|
, |
|
|
|
|
|
|||||
3) |
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. |
Функцию |
|
|
|
, определённую равенством |
|
|
|
|||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
называют производной функции |
. Производную |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
обозначают |
|
ещё , |
|
. Согласно этому равенству |
|
|
для заданных функций |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
получим следующее результаты: |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


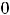

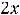 ;
;

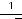 ;
;
3) 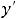

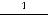


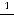 ;
;
4) |
|
= |
. |
При вычислении пределов в случаях 2) 4) совершался переход к пределу
под знаком функций |
|
|
|
|
|
в силу их непрерывности в соответствующих |
||||||
|
|
|
||||||||||
областях определения. |
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: 1) |
|
|
|
|
; 3) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
||||||||||||
|
59 |
|
|
|
|
|||||||

Пример 2. По правилам дифференцирования и таблице производных основных элементарных функций найти производные следующих функций:
1) 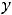

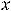
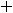
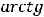
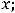
3) 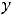

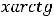
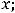
Решение. Выпишем производные участвующих функций в заданных выражениях (согласно таблице производных): 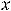


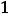
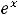


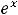
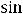
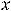



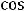
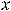
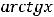


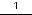 Теперь выпишем необходимые в данном примере правила дифференцирования:
Теперь выпишем необходимые в данном примере правила дифференцирования:
Тогда для заданных функций получим следующие результаты:
1) 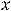
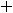
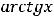


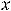

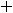
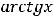


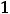
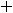
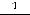
 2)
2) 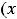
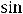
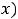


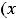
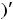
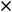
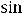
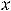
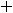
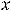
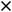
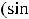
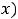


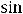
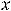
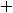
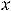
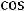
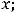
3)
4)
Ответы: 1)
Пример 3. Найти производные следующих сложных функций: 1) |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сложную |
|
функцию |
|
|
|
|
|
можно представить в |
вид |
||||||||||||||||
Решение. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
композиции |
(суперпозиции) двух функций |
|
|
|
|
|
|
|
|
|
, при |
этом |
||||||||||||||||
переменную |
называют промежуточным аргументом. Для её производной |
|||||||||||||||||||||||||||
справедливо |
равенство |
|
|
|
|
где |
|
есть |
производная сложной |
|||||||||||||||||||
функции по |
переменной , |
есть производная |
функции |
|
|
|
по |
|||||||||||||||||||||
переменной |
, а |
|
|
производная функции |
|
|
|
|
по |
. Аналогичное |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
правило верно для любого конечного числа композиций. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Функция |
|
|
|
|
представима в виде |
|
|
|
|
|
. |
|
Так как |
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
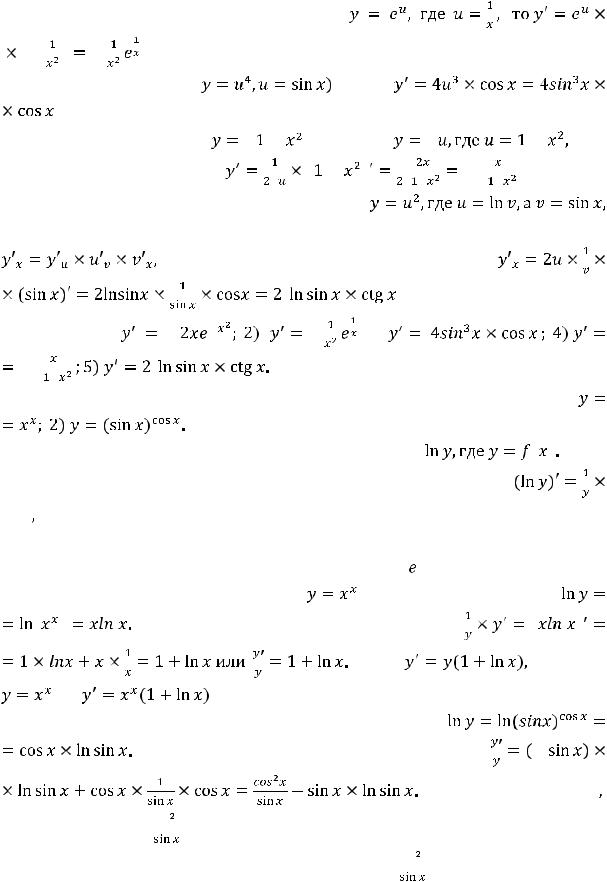
Так как функция 2) представима |
|
в виде |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для третьей функции ( |
|
|
|
|
имеем |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Представив функцию |
|
|
|
|
в виде |
|
|
|
|
|
|
|
по |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
указанному правилу получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последняя функция представляется в виде |
|
|
|
||||||||||||||||||
т.е. она является суперпозицией трёх |
функций. Тогда применяем равенство |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
из которого для данной функции имеем, что |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ответы: 1) |
|
|
|
|
` |
|
|
|
|
|
; 3) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Найти производные степенно-показательных функций: |
1) |
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Пример 4. |
|
|
|||||||||||||||||||
|
Решение. Пусть нужно найти производную функции |
Тогда |
||||||||||||||||||||
по правилу дифференцирования сложной функции имеем равенство |
|
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||
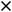
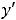 которое называют формулой логарифмического дифференцирования. Эту формулу и используем для прохождения производных заданных функций,
которое называют формулой логарифмического дифференцирования. Эту формулу и используем для прохождения производных заданных функций,
предварительно прологарифмировав их по основанию . |
|
|
|
|
|
|
|||||||
Прологарифмировав функцию |
, получим |
равенство |
|||||||||||
|
|
|
Продиффиринцируем последнее равенство: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Тогда |
|
|
|
|
и так как |
|
, то |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Логарифмируя |
вторую |
функцию, |
получаем |
|
|
|
|
|
|
||||
|
|
|
Дифференцируя это равенство, получаем |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
Так как 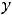

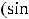
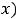
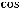

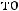
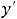

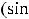
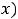
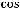

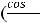


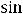
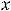
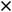
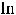
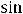
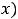 .
.
Ответы: 1) 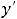

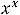
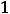
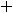
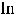
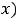

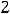
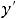

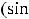
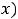
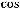

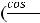


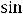
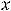
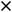
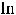
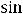
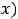 .
.
61

Пример 5. Написать уравнения касательной и нормали к кривой |
|
|
||||
|
|
|||||
в точке с абсциссой |
. |
|
|
|
|
|
Решение. Известно, что уравнение касательной к кривой |
в точке |
|||||
имеет вид |
|
|
|
даёт |
угловой |
|
|
|
|||||
коэффициент этой прямой. Нормаль к кривой – это прямая, проходящая через эту точку и перпендикулярная касательной. Так как угловые коэффициенты
двух |
перпендикулярных прямых связаны |
|
равенством |
|
|
|
|
|
|
то |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнением нормали будет прямая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Таким образом, |
найти |
|
|
|
|
|
|
|
|
для данной функции и подставить эти |
|||||||||||||||||||||||||||||||||||||||||||||||
значения в выписанные уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Сначала найдём |
|
очевидно, что |
|
|
|
|
|
|
|
|
|
. Так как по условию |
, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
, а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
Соответственно |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
получаем |
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
Которые |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
преобразуются к уравнениям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ответы: |
|
|
|
|
|
|
– уравнение касательной; |
|
|
|
|
|
|
|
|
|
|
|
– уравнение |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
нормали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6. |
Найти точки на кривой |
|
|
|
|
|
|
|
|
, в которых касательная |
|||||||||||||||||||||||||||||||||||||||||||||||
1) параллельна оси абсцисс; 2) параллельна прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Решение. Если касательная параллельна оси |
, |
то её угловой коэффициент |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
равен нулю, и тогда |
|
. Так как у данной функции |
, |
то |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
абсциссы таких точек |
являются решениями |
|
|
функционального |
|
уравнения |
|||||||||||||||||||||||||||||||||||||||||||||||||||
. Это уравнение имеет только одно |
решение |
|
|
|
|
|
|
|
|
|
Найдём |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
соответствующую ординату точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Таким |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
образом, точкой на кривой, в которой касательная параллельна оси абсцисс,
является точка |
|
|
Очевидно, что графиком рассматриваемой функции |
|||||
|
||||||||
является парабола; точка |
|
|
является её вершиной. |
|
||||
|
|
|
||||||
Угловым коэффициентом прямой |
|
является число |
. У |
|||||
|
||||||||
касательной к кривой, параллельной этой прямой, должен быть тот же
коэффициент. Тогда |
, т.е. |
имеем уравнение |
, единственным |
|||
решением которого является |
. Вычислив ординату кривой |
, |
||||
получим точки |
. |
|
|
|
||
Ответы: 1) |
|
|
; 2) |
62 |
|
|
|
|
|
||||
|
|
|
|
|
|
|

Пример 7. При объёме |
(в у.е.) выпуска продукции себестоимость (в у.е.) |
|||||||||||||||||||||||||||||||
единицы этой продукции выражается функцией |
|
|
|
|
Найти |
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
эластичность себестоимости при объёме |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Решение. |
Эластичность |
|
|
функции |
определяется равенством |
|||||||||||||||||||||||||||
|
|
|
и показывает, на сколько процентов изменится значение функции |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
при изменении независимой переменной |
|
|
на 1%. |
|
|
|
|
|
|
|
||||||||||||||||||||||
Так как в данном примере |
|
|
|
, |
то |
|
|
|
|
|
|
. Тогда при |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. при объёме выпуска |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
увеличение объёма выпуска на |
приведёт к снижению себестоимости на |
|
. |
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
Ответ: |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример |
8. |
Найти |
точки |
экстремума, точки |
|
перегиба, промежутки |
||||||||||||||||||||||||||
монотонности и выпуклости следующих функций:
1) 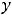

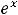

Решение. В данном примере под промежутком будем понимать любое из следующих множеств: 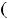

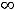
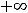
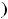 , интервал
, интервал 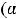
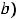 , лучи
, лучи 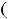

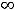
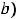 или
или 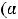
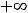
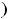 .
.
Если функция на любом таком промежутке дифференцируема (имеет конечную производную) и 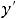
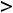
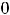
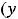

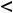
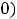 , то она на этом промежутке возрастает (убывает). Если существует вторая производная и
, то она на этом промежутке возрастает (убывает). Если существует вторая производная и 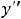
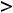
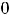
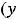
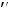
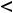
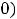 на любом таком промежутке, то кривя на плоскости, заданная функцией
на любом таком промежутке, то кривя на плоскости, заданная функцией 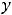

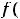
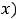 , обращена выпуклостью вниз (вверх).
, обращена выпуклостью вниз (вверх).
В литературе применяются термины «выпуклая кривая» и «выгнутая кривая», однако ввиду разногласий по этим терминам здесь они не применяются.1
Точки области определения непрерывной функции называются её критическими точками первого рода если производная в такой точке либо равна нулю, либо бесконечности, либо вовсе не существует. Критические точки первого рода являются подозрительными на экстремум, однако экстремума в них может и не быть; это увидим при решении задания 4).
1 Выпуклую вверх кривую называют иногда выпуклой, а иногда вогнутой; то же самое относится к кривой, обращённой выпуклостью вниз.
63
Об экстремумах функции, определённой на отрезке 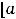
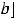 или любом из лучей
или любом из лучей 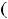

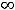
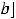 , [
, [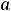
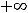
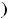 , можно говорить лишь во внутренних точках таких промежутков.
, можно говорить лишь во внутренних точках таких промежутков.
Экстремумы (максимумы и минимумы) функции являются локальными или точечными понятиями. Когда говорим о максимуме (минимуме), то речь идёт о наибольшем (наименьшем) значении функции в точке экстремума 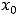 лишь по сравнению с её значениями в достаточно близких к ней точках, т.е. ведётся сравнение значений функции в окрестности
лишь по сравнению с её значениями в достаточно близких к ней точках, т.е. ведётся сравнение значений функции в окрестности 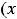


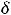
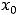
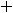
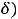 точки
точки 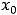 , возможно очень малого радиуса
, возможно очень малого радиуса 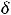 .
.
Когда речь идёт о глобальном экстремуме, то выявляются наибольшее и наименьшее значения функции, если они достигаются, на всей области определения функции или на каком-нибудь промежутке (например, отрезке 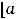
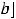 ), являющемся частью её области определения.
), являющемся частью её области определения.
Приведём достаточное условие существования экстремума функций, связанных с понятием её первой производной. В связи с этим говорят о первом правиле исследования на экстремум, пригодном для любой критической точки первого рода.
Пусть функция 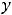

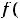
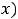 определена в некоторой окрестности критической точки
определена в некоторой окрестности критической точки 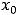 и дифференцируема во всех точках этой окрестности за исключением, может быть, самой точки
и дифференцируема во всех точках этой окрестности за исключением, может быть, самой точки 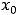 . Если при переходе слева направо через эту точку:
. Если при переходе слева направо через эту точку:
1)производная меняет свой знак с плюса на минус, то в точке 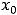 будет максимум (max);
будет максимум (max);
2)производная меняет знак с минуса на плюс, то в точке 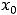 будет минимум
будет минимум
(min);
3)производная своего знака не меняет, то экстремума в точке 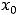 нет.
нет.
Точки 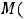
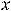
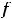
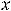
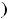 , лежащие на непрерывной кривой
, лежащие на непрерывной кривой 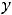

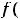
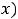 и разделяющие промежутки выпуклости вниз и вверх графика функции, называются точками перегиба.
и разделяющие промежутки выпуклости вниз и вверх графика функции, называются точками перегиба.
В точке перегиба касательная к кривой, если она существует, пересекает эту кривую. В точке перегиба могут быть односторонние касательные или вертикальная касательная.
Внутренние точки области определения непрерывной функции 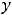

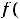
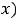 называются её критическими точками второго рода, если вторая производная
называются её критическими точками второго рода, если вторая производная
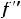
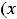
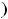 в этих точках равна нулю или бесконечности, или вовсе не существует. На кривой с такими абсциссами возможны точки перегиба, но их может и не быть.
в этих точках равна нулю или бесконечности, или вовсе не существует. На кривой с такими абсциссами возможны точки перегиба, но их может и не быть.
64

Укажем теперь достаточное условие существования точки перегиба на непрерывной кривой.
Пусть 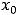 есть критическая точка второго рода непрерывной функции
есть критическая точка второго рода непрерывной функции 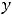


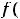
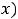 и в некоторой окрестности этой точки за исключением, может быть, её самой, существует конечная вторая производная. Если при переходе через
и в некоторой окрестности этой точки за исключением, может быть, её самой, существует конечная вторая производная. Если при переходе через
вторая производная |
сменит свой знак, то на кривой будет точка перегиба |
||
. Если |
в окрестности |
вторая |
производная имеет одинаковые |
знаки, то на кривой нет точки перегиба. |
|
|
|
Заметим, что исследование функции |
на выпуклость и перегиб с |
||
помощью второй производной |
аналогично исследованию функции на |
||
экстремум с помощью первой производной |
. |
|
|
|
||
Если |
есть точка разрыва функции, то над ней на кривой точки перегиба |
|||||
нет, однако при переходе через |
направление выпуклости может измениться |
|||||
(см. следующий пример). |
|
|
|
|
|
|
Переходим к изучению заданных функций. |
|
|
|
|
||
Функция |
определена и непрерывна на всей числовой оси |
|
|
, |
||
|
||||||
причём |
. Во |
внутренних |
точках области определения |
обе |
||
производные существуют и не обращаются в нуль. Следовательно, у функции нет критических точек ни первого, ни второго рода. Экстремумов нет и так как
на |
|
|
|
|
, то функция возрастает на области определения. Так |
||||
|
|
|
|||||||
как |
|
, то функция на области определения выпукла вниз. Точек |
|||||||
перегиба нет. Её график изображён на рисунке 18. |
|
|
|||||||
Функция |
|
|
|
|
определена и непрерывна на луче |
. |
В этом |
||
промежутке |
|
|
|
|
существует и не обращается в нуль. Нет критических точек |
||||
|
|
|
|
||||||
первого рода, |
тогда нет и экстремумов. Так как |
|
|
на |
, то |
||||
|
|||||||||
функция на области определения возрастает. Вторая производная 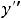

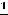



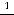 также существует и не обращается в нуль на
также существует и не обращается в нуль на 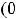
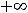
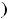 . Точек перегиба нет.
. Точек перегиба нет.
Так как |
|
|
|
на |
, то на этом луче график функции имеет |
|
|
|
выпуклость вверх. График изображён на рисунке 17.
Функция 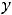

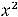 определена и непрерывна на
определена и непрерывна на 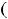

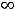
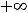
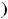 . При этом первая производная
. При этом первая производная 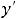

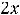 определена на том же множестве. Тогда экстремум может быть только в стационарных точках, т.е. точках, где первая производная обращается в нуль. Очевидно, что такой точкой является только
определена на том же множестве. Тогда экстремум может быть только в стационарных точках, т.е. точках, где первая производная обращается в нуль. Очевидно, что такой точкой является только 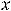

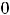 . При
. При
65
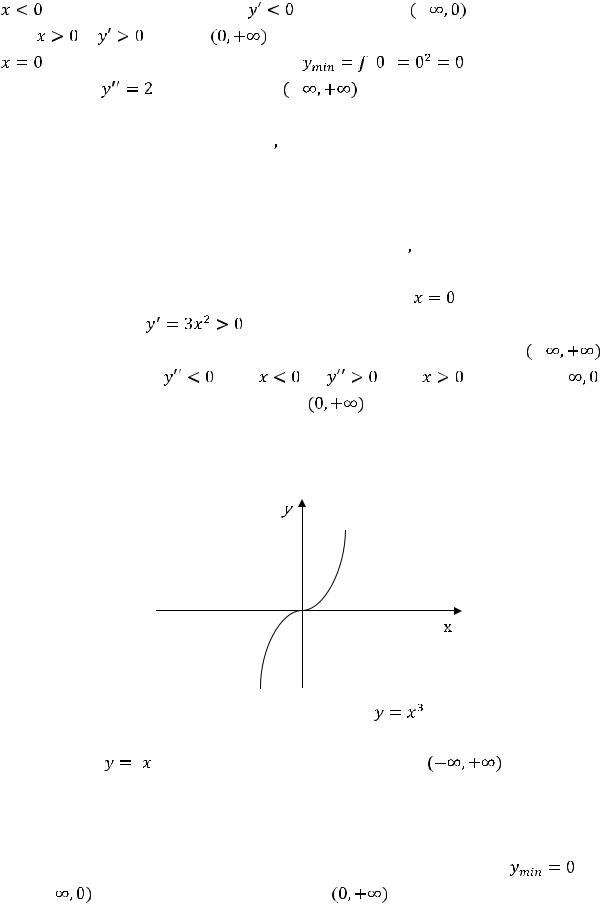
|
выполняется неравенство |
|
, тогда на луче |
|
|
функция убывает. |
||
|
|
|
||||||
При |
и |
на луче |
функция возрастает. Таким образом, в точке |
|||||
|
имеется минимум. При этом |
. |
Так как вторая |
|||||
производная |
существует на |
|
|
и не обращается в нуль, то нет |
||||
|
|
|||||||
критических точек второго рода; следовательно, на кривой нет точек перегиба. Ввиду того что 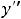

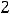
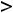
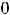 на
на 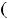

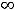
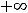
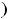 , график функции является выпуклым вниз. График этой функции известен читателю. Им является парабола с вершиной в начале координат, ветвь направлена вверх, а ось ординат есть ось симметрии графика.
, график функции является выпуклым вниз. График этой функции известен читателю. Им является парабола с вершиной в начале координат, ветвь направлена вверх, а ось ординат есть ось симметрии графика.
Функция 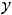

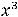 и её производные
и её производные 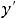

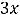
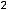
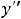

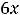 определены и непрерывны на всей числовой оси. Очевидно, что единственной критической
определены и непрерывны на всей числовой оси. Очевидно, что единственной критической
точкой как первого, так и второго рода является точка |
. Экстремума в этой |
|||||||||||
точке нет, так как |
в любой окрестности этой точки (производная |
|||||||||||
при переходе через точку знак не меняет). Функция возрастает на |
|
. |
||||||||||
|
||||||||||||
Вторая производная |
при |
и |
при |
. На луче |
|
|
|
|||||
|
|
|
||||||||||
будет выпуклость вверх, а на луче |
|
выпуклость |
вниз. |
Начало |
||||||||
|
||||||||||||
координат (0,0) является точкой перегиба. |
|
|
|
|
|
|
|
|
||||
График функции |
называется |
кубической |
|
параболой и |
изображён на |
|||||||
рисунке 22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
Рисунок 22 – График функции |
|
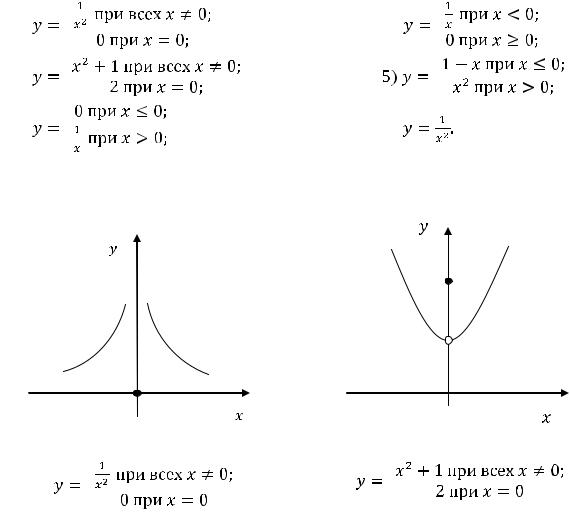
Функция |
определена и непрерывна на |
. Её график |
изображён на рисунке 1. Из графика видно, что в точке (0, 0) график не имеет касательной (односторонние касательные существуют). В точке 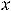

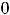 нет ни конечной, ни бесконечной производной. Эта точка является критической точкой
нет ни конечной, ни бесконечной производной. Эта точка является критической точкой
первого рода. Очевидно, что в точке имеется минимум; при этом |
. На |
||
луче (- |
функция убывает, а на луче |
возрастает. Всё это можно |
|
|
66 |
|
|

установить и с помощью первого правила исследования на экстремум.
Действительно, у этой функции |
при |
и |
при |
. |
||
Точка |
является также единственной критической точкой второго рода |
|||||
этой функции, так как |
не существует. Однако о выпуклости этой функции |
|||||
не принято говорить, так как касательная в любой точке этой кривой, кроме точки 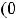
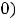 , совпадает с самой кривой (см. рисунок 22). График кривой лежит не ниже и не выше любой её касательной, а совпадает с ней. Здесь имелось в виду определение выпуклости кривой с помощью касательной. При других определениях выпуклости (с помощью хорд или неравенств) также невозможно говорить о промежутках выпуклости той функции. Линейные и постоянные функции на промежутках можно считать как выпуклыми вниз, так и выпуклыми вверх. При других определениях выпуклости (с помощью хорд или неравенств) также невозможно говорить о промежутках выпуклости этой функции. Линейные и постоянные функции на промежутках можно считать как выпуклыми вниз, так и выпуклыми вверх.
, совпадает с самой кривой (см. рисунок 22). График кривой лежит не ниже и не выше любой её касательной, а совпадает с ней. Здесь имелось в виду определение выпуклости кривой с помощью касательной. При других определениях выпуклости (с помощью хорд или неравенств) также невозможно говорить о промежутках выпуклости той функции. Линейные и постоянные функции на промежутках можно считать как выпуклыми вниз, так и выпуклыми вверх. При других определениях выпуклости (с помощью хорд или неравенств) также невозможно говорить о промежутках выпуклости этой функции. Линейные и постоянные функции на промежутках можно считать как выпуклыми вниз, так и выпуклыми вверх.
Функция |
|
|
|
|
|
|
определена и |
непрерывна |
на |
|
|
. |
Её |
первая |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||
производная |
|
|
|
|
|
|
стационарных |
критических |
точек не имеет, так как, |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
очевидно, |
.Точка |
является |
единственной |
критической |
точкой |
|||||||||||||||||||
первого рода, поскольку |
. |
На луче |
|
|
|
|
|
|
выполняется неравенство |
|||||||||||||||
|
||||||||||||||||||||||||
, функция на этом промежутке убывает. |
На луче |
функция |
||||||||||||||||||||||
возрастает, так как на этом промежутке |
. Таким образом, функция в точке |
|||||||||||||||||||||||
имеет минимум; при этом |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вторая |
производная имеет |
вид |
|
|
|
|
|
|
|
|
, |
|
причём |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
Следовательно, точка |
есть |
|
критическая |
точка |
|
второго |
рода для |
|||||||||||||||||
исследуемой функции. |
При любых значениях |
вторая |
производная |
|||
отрицательна ( |
). |
График функции на промежутках |
|
|
и |
|
|
||||||
будет выпуклым вверх. Точка (0,0), подозрительная на перегиб, таковой не является.
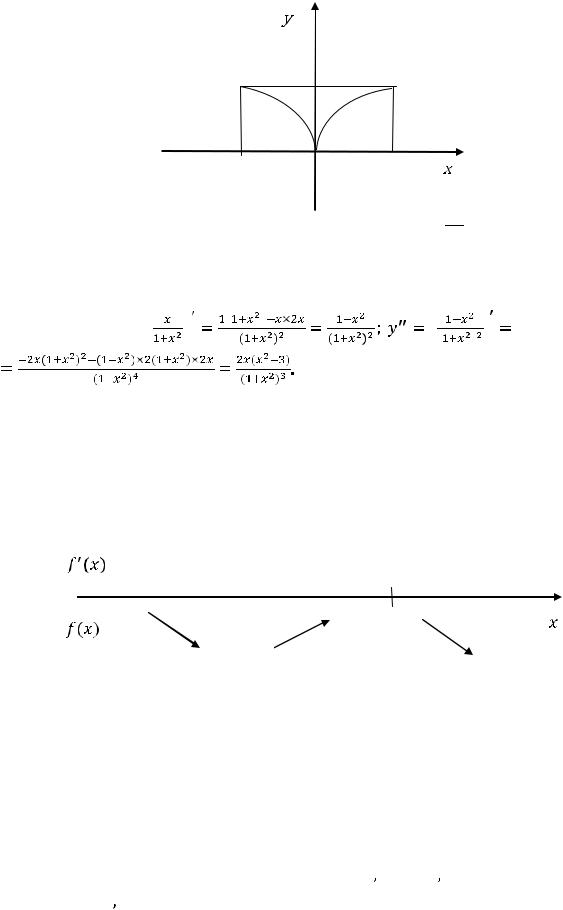
Ниже построен график функции |
|
(рисунок 23). При построении |
учтено, что функция чётна. |
|
|
67
1
0
-1 |
1 |
Рисунок 23 –График функции 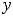

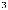
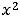
Теперь исследуем функцию 7). Находим её первую и вторую
производные: 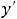

Сама функция и обе производные определены на всей числовой оси.
Так как первая производная всюду существует, то надо находить только стационарные точки. Необходимое условие 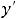

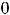 приводит к решению уравнения
приводит к решению уравнения 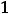

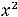

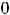 , очевидными корнями которого являются
, очевидными корнями которого являются 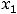


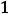 и
и
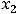

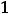 . Для дальнейшего исследования на монотонность и экстремум делаем следующий рисунок 24.
. Для дальнейшего исследования на монотонность и экстремум делаем следующий рисунок 24.
- |
|
+ |
- |
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
1 |
|
|
|
|
|
|
|
min |
|
max |
|
|
|
|
|
||
|
|
|
|
|
Рисунок 24 – Геометрическая интерпретация исследования функции на монотонность и экстремум
Над осью 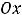 ставится знак первой производной на соответствующем промежутке. При этом знак производной сохраняется для всех точек рассматриваемого промежутка, поэтому его достаточно найти в какой-нибудь точке этого промежутка. Ниже оси
ставится знак первой производной на соответствующем промежутке. При этом знак производной сохраняется для всех точек рассматриваемого промежутка, поэтому его достаточно найти в какой-нибудь точке этого промежутка. Ниже оси 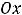 стрелкой помечается тип монотонности. Стрелка вниз означает убывание, а вверх – возрастание на промежутке.
стрелкой помечается тип монотонности. Стрелка вниз означает убывание, а вверх – возрастание на промежутке.
Итак, функция убывает на промежутках 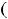

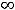

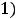 ,
, 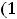
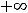
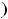 и возрастает на интервале
и возрастает на интервале 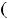

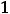
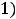 . В точке
. В точке 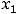


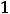 она имеет минимум, а в точке
она имеет минимум, а в точке 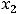

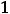

68
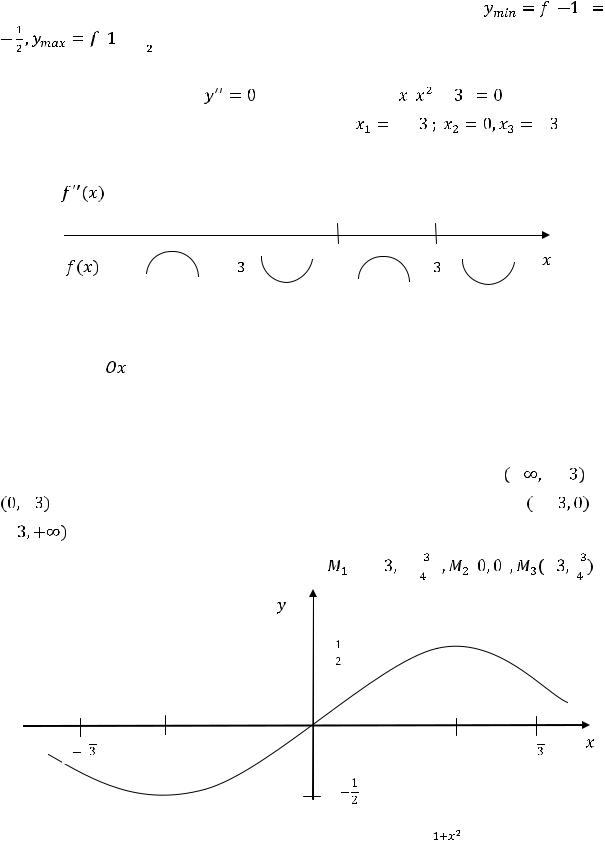
максимум, значения функции в точках экстремума таковы:

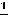 .
.
Так как вторая производная всюду существует, то критические точки второго
рода находятся из условия |
|
|
, т.е. из уравнения |
|
|
. Корни этого |
|||||||||||
|
|
||||||||||||||||
уравнения в порядке возрастания таковы: |
|
|
|
|
|
|
|
|
|
. Для |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
дальнейшего исследования на выпуклость и перегибы делаем рисунок 25. |
|||||||||||||||||
|
- |
|
+ |
- |
|
|
|
|
+ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рисунок 25 |
|
Геометрическая интерпретация исследования |
|||||||||||||||
|
|||||||||||||||||
|
|
|
функции на выпуклость |
|
|
|
|
|
|
|
|
|
|
||||
Над осью |
расставляем знаки второй производной на соответствующих |
||||||||||||||||
промежутках, ниже оси помечаем дугами направления выпуклости. Знак второй производной достаточно найти в какой-нибудь одной точке каждого промежутка, в остальных точках этого промежутка будет такой же знак.
|
Из рисунка 25 делаем следующий вывод. На промежутках |
|
|
|
|
|
|
|
|
|
|
|
и |
|||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
график функции является выпуклым вверх, а на промежутках |
|
|
|
|
|
|
|
|
|
|
и |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
( |
|
|
|
|
|
выпуклым вниз. На кривой, примерный график которого изображён |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
на рисунке 26, имеются три точки перегиба |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
-1
1
Рисунок 26 – График функции 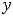

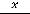 Функция нечётна, её график симметричен относительно начала координат.
Функция нечётна, её график симметричен относительно начала координат.
69
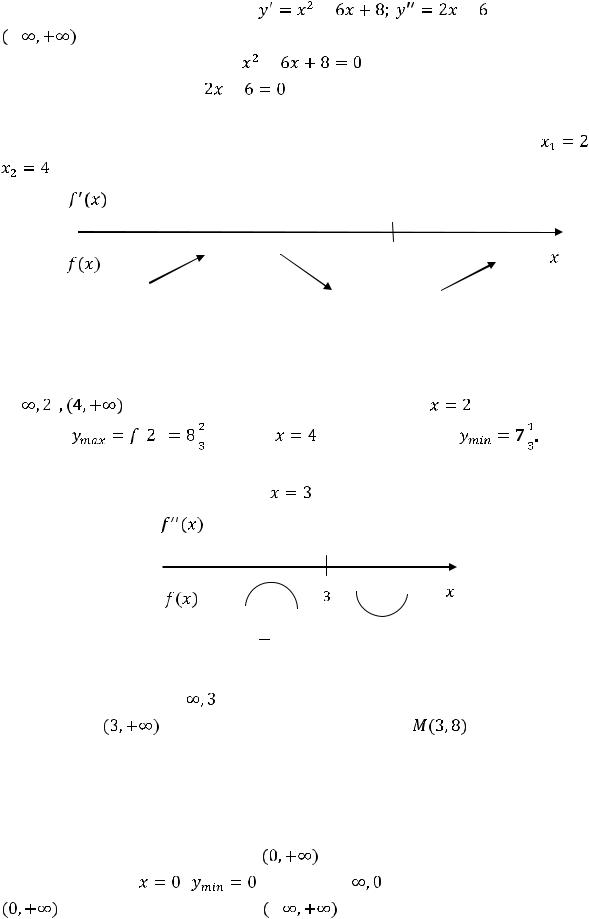
|
|
Функция 8) и её производные |
|
|
|
|
|
определены на |
||
|
|
|
|
|||||||
|
|
. Тогда критические точки первого рода (стационарные точки) есть |
||||||||
|
|
|||||||||
корни квадратного уравнения |
|
|
|
, а критические точки второго |
||||||
|
|
|
||||||||
рода есть корни уравнения |
|
|
. |
|
|
|
|
|||
|
|
|
|
|
||||||
Проведём исследование на монотонность и экстремум по аналогии с
предыдущей функцией, отметив на оси абсцисс стационарные точки |
и |
|||||||||||
|
|
(см.рисунок 27). |
|
|
|
|
|
|
||||
|
|
|
+ |
|
|
|
|
|
- |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
4 |
|
|
|
||
|
|
|
|
|
min |
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рисунок 27 |
|
Геометрическая интерпретация |
|
||||||
|
|
|
|
|
||||||||
|
|
исследования функции на монотонность и экстремум |
|
|||||||||
|
|
Из рисунка |
27 видно, |
что |
функция возрастает |
на промежутках |
||||||
|
|
|
и убывает на интервале (2, 4). В точке |
имеет максимум, |
||||||||
|
|
|
||||||||||
при этом |
|
|
. В точке |
имеет минимум, а |
|
|
|
|||||
|
|
|
|
|
||||||||
Теперь проведём исследование на выпуклость и перегибы. Критической
точкой второго рода является точка |
. |
+ |
- |
Рисунок 28 Геометрическая интерпретация
|
|
|
исследования функции на выпуклость |
|
На промежутке |
|
график обращён выпуклостью вверх, а на |
||
|
||||
промежутке |
|
|
выпуклостью вниз. Точка |
является точкой |
|
|
|||
перегиба. |
|
|
|
|
Рекомендуем читателю построить примерный график этой функции. Ответы: 1) нет точек экстремума и точек перегиба, функция на её области
определения возрастает и выпукла вниз; 2) нет точек экстремума и перегиба,
функция на области определения |
|
|
|
возрастает и выпукла вверх; 3) имеет |
|||
минимум в точке |
, |
, на луче |
|
|
функция убывает, а на луче |
||
|
|
||||||
возрастает; |
график на |
|
|
|
|
|
обращён выпуклостью вниз; 4) |
70 |
|
|
|||||
|
|
|
|
|
|||

возрастает на всей числовой оси, экстремумов нет; начало координат является
точкой перегиба; 5) на |
|
|
|
функция убывает, на |
возрастает; в точке |
|||
|
||||||||
|
имеется минимум, при этом |
; 6) |
эта функция имеет минимум при |
|||||
, |
; на луче |
|
|
она убывает, |
а на луче |
возрастает; на |
||
|
|
|||||||
этих промежутках график является выпуклым вверх, точек перегиба нет; 7)
функция убывает на промежутках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и возрастает на интервале |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
(-1, 1); в точке |
|
имеет минимум, а в точке |
|
максимум; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
; на промежутках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
график функции является |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
выпуклым вверх, а на промежутках, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выпуклым вниз; на |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
кривой имеются три точки перегиба |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 8) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
функция возрастает на промежутках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и убывает на интервале |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
(2,4); в точке |
|
|
имеет максимум |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а в точке |
|
|
минимум |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
( |
|
|
|
|
|
|
на промежутке |
|
|
|
график является выпуклым вверх, а на |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
промежутке |
- |
выпуклым вниз; |
|
|
|
|
|
|
|
|
|
|
есть точка перегиба графика |
||||||||||||||||||||||||||||||||||||||
кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Замечание. При исследовании функций примера 8 на экстремум предполагалась их непрерывность в любой критической точке первого рода. однако в определении экстремума в точке 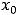 не предполагается непрерывность в
не предполагается непрерывность в
самой этой точке; требуется только, чтобы функция в точке |
была определена. |
||
Приведём это определение. |
|
|
|
Точка является точкой максимума (минимума) функции |
, если можно |
||
указать такую окрестность |
|
этой точки, возможно малого радиуса |
|
|
|||
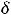 , что для всех точек
, что для всех точек 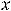 из этой окрестности будет выполняться неравенство
из этой окрестности будет выполняться неравенство
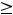
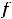
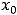
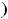 . В случае строгих неравенств
. В случае строгих неравенств 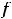
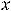
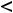
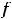
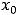 или
или
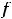
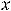
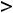
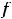
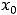 соответствующий экстремум называется собственным или строгим. Строгий экстремум встречается наиболее часто в примерах.
соответствующий экстремум называется собственным или строгим. Строгий экстремум встречается наиболее часто в примерах.
Итак, требуется проводить отдельное исследование на экстремум тех точек, в которых функция определена, но имеет разрыв.
При исследовании функции на монотонность надо обращать внимание и на точки, в которых функция определена, но имеет разрыв.
При исследовании функции на монотонность надо обращать внимание и на точки, в которых функция не определена, но которые являются предельными точками (точками сгущения) её области определения. Такие точки разрыва 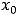
71
надо отмечать на оси абсцисс. Так как функция в 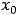 не определена, то об экстремуме в этой точке говорить нельзя. Однако характер монотонности при переходе через
не определена, то об экстремуме в этой точке говорить нельзя. Однако характер монотонности при переходе через 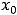 может измениться. Такое бывает даже в случаях, если функция в выколотой окрестности точки
может измениться. Такое бывает даже в случаях, если функция в выколотой окрестности точки 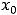 задана одним аналитическим выражением. Тем более это может случиться, если функция левее и правее точки
задана одним аналитическим выражением. Тем более это может случиться, если функция левее и правее точки 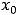 задана различными формулами. Если вид монотонности при переходе через такую
задана различными формулами. Если вид монотонности при переходе через такую 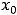 не меняется, то промежуток монотонности не будет единым, а будет состоять из объединения промежутков. Это замечание относится и к исследованию функции на выпуклость.
не меняется, то промежуток монотонности не будет единым, а будет состоять из объединения промежутков. Это замечание относится и к исследованию функции на выпуклость.
Пример 9. Исследовать на экстремум, монотонность и выпуклость следующие функции:
1) |
|
4) |
|
2) |
|
|
|
3) |
|
6) |
|
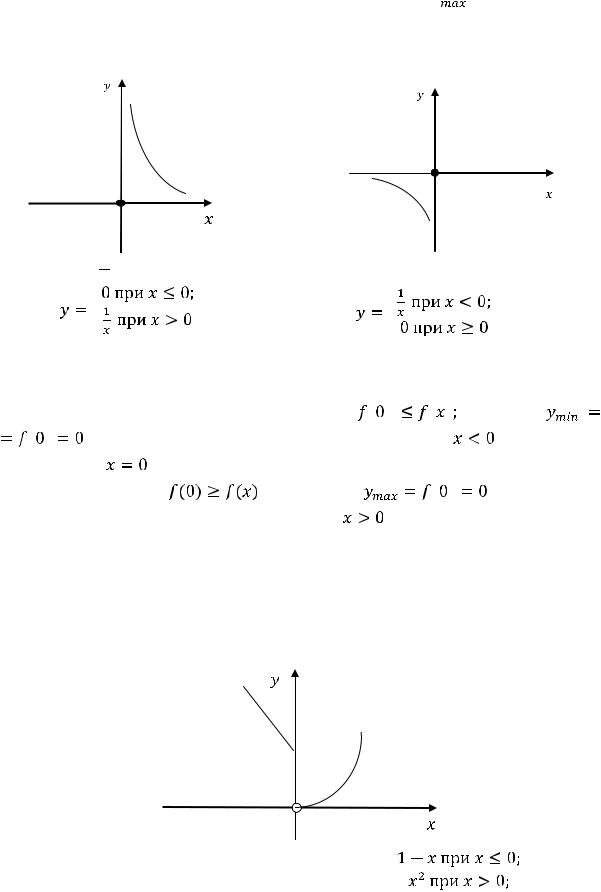
Решение. Ниже на рисунках 29 и 30 изображены графики функций 1) и 2).
|
2 |
|
1 |
0 |
0 |
Рисунок 29 – График функции |
Рисунок 30 – График функции |
Обе функции в точке 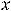

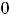 определены, имеют в ней разрыв и строгие экстремумы. Для функции 1) в любой окрестности нуля выполняется неравенство
определены, имеют в ней разрыв и строгие экстремумы. Для функции 1) в любой окрестности нуля выполняется неравенство 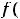
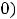
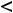
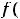
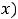 . Т.е. имеется строгий минимум (
. Т.е. имеется строгий минимум (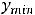

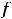
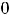

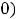 . Для функции 2,) есть окрестность нуля, в которой выполняется неравенство
. Для функции 2,) есть окрестность нуля, в которой выполняется неравенство 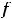
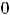
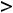
72
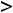
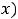 , т.е. имеется строгий локальный максимум (
, т.е. имеется строгий локальный максимум (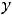

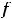
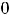

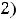
 По графикам легко указать промежутки монотонности и выпуклости этих функций.
По графикам легко указать промежутки монотонности и выпуклости этих функций.
Построим графики функций 3) и 4) (рисунки 31 и 32).
0
0
Рисунок 31 График функции Рисунок 32 – График функции
Обе функции в точке 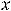

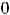 определены, имеют разрыв и не строгие экстремумы. Функция 3) имеет в этой точке минимум, т.к. имеется окрестность
определены, имеют разрыв и не строгие экстремумы. Функция 3) имеет в этой точке минимум, т.к. имеется окрестность
нуля, где выполняется не строгое неравенство |
|
при этом |
|||
(это значение функция принимает и при всех |
). Функция 4) |
||||
имеет в точке |
максимум, т.к. имеется её окрестность, где выполняется не |
||||
строгое неравенство |
; при этом |
|
(это |
нулевое |
|
значение является и значением при всех |
). Предоставляем |
читателю |
|||
указать промежутки монотонности и выпуклости этих функций. |
|
||||
Функция 5), график которой изображён на рисунке 33, определена в точке 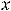

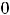 и имеет в ней разрыв. Экстремума в этой точке нет, хотя производная и меняет знак при переходе через эту току. Очевидны промежутки монотонности и выпуклости этой функции.
и имеет в ней разрыв. Экстремума в этой точке нет, хотя производная и меняет знак при переходе через эту току. Очевидны промежутки монотонности и выпуклости этой функции.
 1
1
0
Рисунок 33 – График функции 

73

Функция 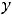

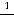 в точке
в точке 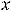

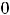 не определена, и поэтому нельзя говорить об экстремуме в этой очке. График функции легко построить, глядя на график функции 1) этого примера. Очевидно, что в точке
не определена, и поэтому нельзя говорить об экстремуме в этой очке. График функции легко построить, глядя на график функции 1) этого примера. Очевидно, что в точке 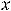

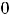 имеется разрыв второго рода. Из-за разрыва нельзя говорить и о точке перегиба на кривой с абсциссой
имеется разрыв второго рода. Из-за разрыва нельзя говорить и о точке перегиба на кривой с абсциссой 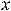

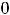 . Однако точку
. Однако точку 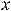

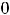 (предельную точку области определения функции) надо учитывать при установлении промежутков монотонности и выпуклости этой функции. Эти промежутки можно установить по знакам
(предельную точку области определения функции) надо учитывать при установлении промежутков монотонности и выпуклости этой функции. Эти промежутки можно установить по знакам 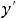


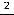
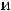
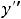

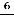 левее и правее нуля. Выводы очевидны из графика функции. Эта функция возрастает на луче
левее и правее нуля. Выводы очевидны из графика функции. Эта функция возрастает на луче 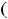

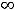
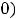 и убывает на луче
и убывает на луче 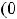
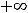
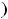 , т.е. характер монотонности при переходе через точку
, т.е. характер монотонности при переходе через точку 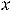

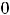 изменился. На этих лучах график функции расположен выпуклостью вниз. Характер выпуклости при переходе через точку
изменился. На этих лучах график функции расположен выпуклостью вниз. Характер выпуклости при переходе через точку 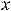

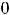 не изменился. Однако промежуток выпуклости не является единым (сплошным). Множеством выпуклости графика функции вниз является множество
не изменился. Однако промежуток выпуклости не является единым (сплошным). Множеством выпуклости графика функции вниз является множество 
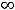
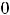
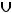
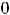
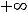 т.е. объединение двух лучей.
т.е. объединение двух лучей.
Ответы: 1) функция имеет строгий минимум в точке 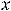

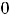 ; 2) в точке
; 2) в точке 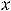

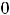 функция имеет строгий максимум; 3) в точке
функция имеет строгий максимум; 3) в точке 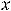

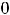 имеется не строгий минимум; 4) в нуле функция имеет не строгий максимум; 5) в нуле экстремума нет; 6) экстремумов нет.
имеется не строгий минимум; 4) в нуле функция имеет не строгий максимум; 5) в нуле экстремума нет; 6) экстремумов нет.
Пример 10. Найти глобальные экстремумы следующих функций:
1) |
2) |
3) |
4) |
Решение. В отличие от локального экстремума глобальным экстремумом называется наименьшее либо наибольшее значение функции на некотором промежутке. Эти значения (одно или оба) могут на рассматриваемом промежутке и не достигаться. Это и покажут задания этого примера.
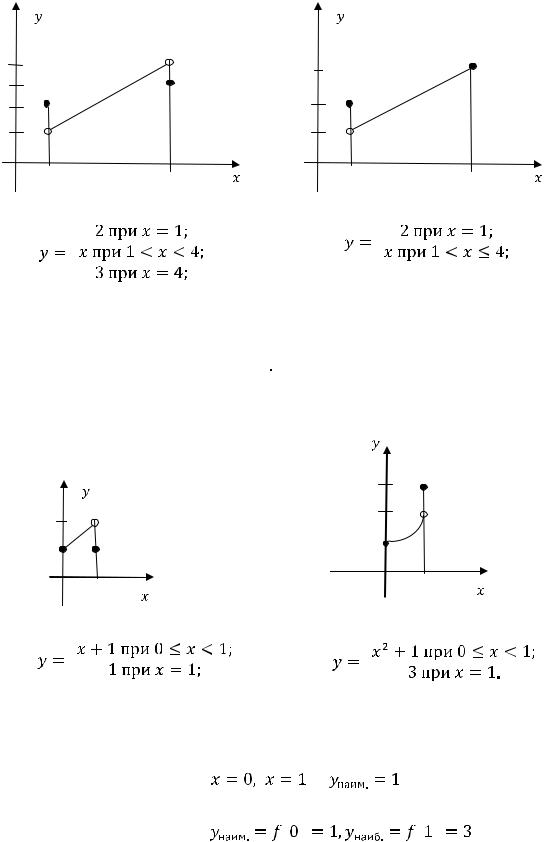
Первая функция задана на отрезке [1, 4] и не имеет на этом отрезке ни наименьшего, ни наибольшего значения (см. график, изображённый на рисунке
34).
74
4 |
|
4 |
|
|
|
|
|
3 |
|
|
|
2 |
|
2 |
|
1 |
|
1 |
|
|
|
|
|
1 |
4 |
1 |
4 |
Рисунок 34 – График функции |
Рисунок 35 – График функции |
||
Вторая функция изображена на рисунке 35. Она определена на отрезке [1, 4] и не достигает на нём наименьшего значения. Наибольшее значение функция принимает в точке 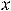

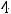 , при этом
, при этом 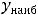

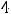 .
.
Исследуем теперь функции 3) и 4), графики которых изображены на рисунках
36 и 37.
|
|
3 |
|
|
2 |
2 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
||
Рисунок 36 – График функции |
Рисунок 37 – График функции |
||
Функция 3), определённая на отрезке [0, 1], не принимает на нём наибольшего значения. Наименьшее значение на этом отрезке достигается,
причём в двух концевых точках |
, и |
. |
Последняя функция, заданная на отрезке |
[0, 1], имеет как наименьшее, так и |
|
наибольшее значение; при этом |
|
. |
Отметим, что все четыре функции этого примера принимают какое-нибудь значение в каждой точке соответствующего отрезка [a, b], но имеют разрывы.
75
Кроме того, все функции являются ограниченными на соответствующем отрезке. Надо ещё иметь в виду, что определённая на отрезке функция может быть неограниченной, тогда глобальные экстремумы (один из них или оба) не достигаются.
Ответы: 1) глобальных экстремумов нет; 2) функция не имеет наименьшего
значения, |
3) |
достигается в точках |
, а |
наибольшего значения нет; 4) |
. |
|
|
Рассмотрим теперь пример исследования на глобальный экстремум непрерывных на отрезке функций.
Пример 11. Найти на указанных промежутках глобальные экстремумы
следующих функций: |
|
|
|
|
|
|
|
|
||||||
1) |
|
|
|
|
|
|
; |
2) |
|
|
|
|
; |
|
|
|
|
|
|
|
|||||||||
3) |
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) |
|
|
|
|
|
|
на отрезках [-2, 2] и [-2, 3]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. В отличие от разрывных функций определённая и неопределённая на отрезке функция будет ограниченной и достигать на нём своих наименьшего и наибольшего значений. Это есть утверждение теорем Вейерштрасса.
Все функции этого примера являются непрерывными на заданных отрезках. Наибольшее значение такой функции может достигаться либо внутри отрезка
(тогда оно достигается в одной или нескольких точках локального максимума, если такие существуют), либо на концах отрезка (одном из концов или обоих). Аналогичное заключение справедливо и о наименьшем значении функции.
Возможны следующие ситуации:
-оба значения достигаются на концах отрезка, каждое из них на одном из концов;
-оба значения достигаются внутри отрезка, это будет в точках локальных экстремумов;
-одно из значений достигается внутри отрезка, а другое – на конце (одном или обоих).
Следовательно, для нахождения глобальных экстремумов непрерывной функции 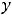

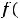
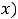 на отрезке [a, b] нужно:
на отрезке [a, b] нужно:
-найти на интервале (a, b) все критические точки первого рода;
-провести исследование этих точек на локальный экстремум;
-вычислить значения функций в критических точках и на концах отрезка, то есть вычислить 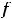
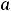
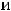
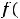
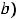 ;
;
76

Из |
всех найденных |
( как правило, их будет конечное число) и |
|
чисел |
выбрать наименьшее (это будет |
) и наибольшее (это будет |
|
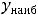 ).
).
Очевидно, что для упрощения исследования пункт 2) описанной процедуры можно исключить. Глобальные экстремумы обязательно будут обнаружены, так как они достигаются либо в критических точках, либо на концах отрезка.
Критической точкой первой функции является только точка 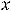

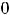 принадлежащая данному отрезку [-2, 2]; экстремума в этой точке нет ввиду строгого возрастания функции. Тогда глобальные экстремумы достигаются на
принадлежащая данному отрезку [-2, 2]; экстремума в этой точке нет ввиду строгого возрастания функции. Тогда глобальные экстремумы достигаются на
концах отрезка. Очевидно, что |
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, что функция |
внутри заданного отрезка имеет локальные |
||||||||||||||||||||||
экстремумы в точках |
|
|
|
|
|
|
|
, при этом |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
На концах отрезка |
|
|
|
|
|
|
|
|
Следовательно, имеем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ситуацию, когда глобальные экстремумы достигаются внутри отрезка среди
точек локальных экстремумов. В данном задании
= |
|
|
Третья функция |
в точке |
имеет локальный минимум |
, |
а на концах отрезка [-1, 1] принимает равные значения |
|
|
|
|||
. |
Таким образом, наименьшее значение она принимает внутри |
||
отрезка, а именно в точке |
локального минимума ( |
= |
|
|
|
|
|||||
наибольшего |
значения достигает |
на обоих концах отрезка |
( |
|
|
|
|||||
|
|
|
|||||||||
Очевидно, |
что функция |
|
|
|
на отрезке [-1, |
1] |
имеет |
локальный |
|||
|
|
||||||||||
максимум в единственной точке |
|
. При этом |
|
4. |
На концах |
||||||
отрезка значения функции |
таковы: |
|
|
. |
Как и |
в третьем |
|||||
|
|||||||||||
задании, наблюдаем ситуацию 3): один из глобальных экстремумов достигается внутри отрезка, а другой – на конце отрезка. В данном задании 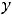

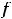

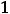


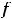
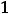

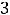 , т.е. наименьшее значение достигается на обоих концах отрезка, а
, т.е. наименьшее значение достигается на обоих концах отрезка, а
функция приняла внутри отрезка в точке
локального максимума. |
|
|
|
Исследуем функцию 5). Так как её производная |
|
|
существует на |
|
|
||
(- ,+ ), то остаётся найти стационарные точки, |
т.е. точки, где |
||
77 |
|
|
|
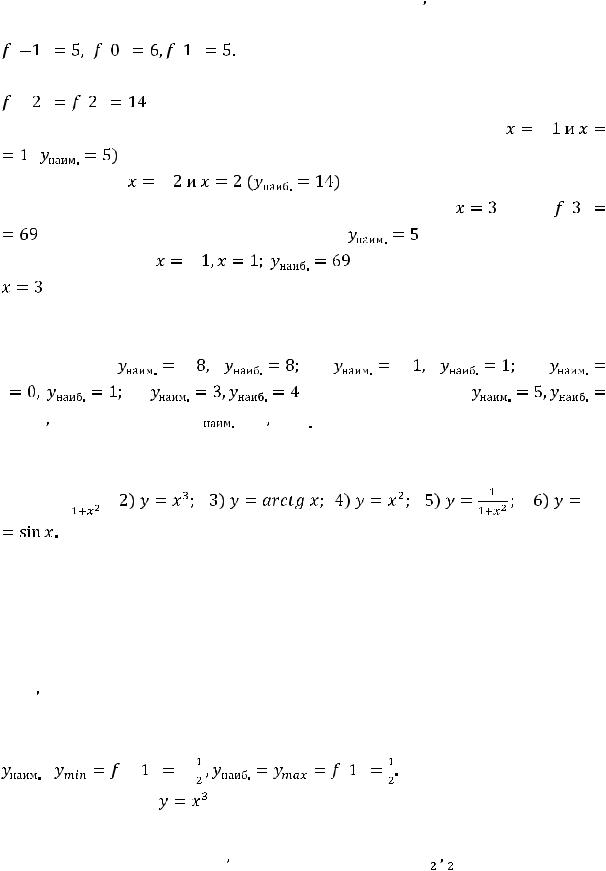
Уравнение , 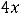
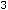

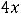

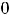 имеет три корня
имеет три корня 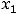 =-1,
=-1, 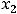

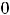
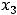

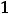 . Исследовать на экстремум их не будем. Найдём только значения функции в этих точках:
. Исследовать на экстремум их не будем. Найдём только значения функции в этих точках:
Найдём глобальные экстремумы функции 5) на отрезке [-2, 2]. Очевидно, что
|
|
|
(данная функция чётная). Тогда наименьшее значение |
||||||||||||
|
|
|
|||||||||||||
функции достигается внутри этого отрезка, при этом в двух точках |
|
|
|||||||||||||
|
|
||||||||||||||
( |
. Наибольшее значение функция имеет на конце отрезка, |
причём |
|||||||||||||
на обоих концах |
|
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||
|
Теперь рассмотрим эту функцию на отрезке [-2, 3]. При |
имеем |
|
||||||||||||
. |
На этом отрезке |
имеем следующее: |
|
|
и |
принимается |
в двух |
||||||||
внутренних точках |
|
|
|
и достигается на правом конце |
|||||||||||
|
|
|
|||||||||||||
|
|
|
этого отрезка. |
|
|
|
|
|
|
|
|
|
|||
|
Рекомендуем построить графики для всех заданий примера. |
|
|||||||||||||
|
Ответы: 1) |
|
|
2) |
|
|
|
3) |
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
4) |
|
|
|
|
|
; 5) на отрезке [-2, 2] |
|
|||||

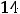 а на отрезке [-2, 3]
а на отрезке [-2, 3] 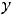

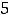
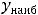

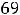
 Пример 12. Исследовать на глобальный экстремум следующие функции в
Пример 12. Исследовать на глобальный экстремум следующие функции в
областях их определения:
1)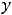

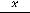

Решение. Функция в своей области определения может достигать глобального экстремума (любого из них или обоих), а может и не достигать, даже если она непрерывна и ограничена. Это и выяснится из заданий данного примера.
Все функции примера определены и непрерывны на всей числовой оси
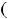

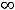
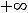
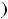 .
.
График первой функции изображён на рисунке 26. Функция является
ограниченной и достигает |
своего наибольшего |
|
и наименьшего значений: |
||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График функции |
изображён на рисунке |
22. На области определения |
|||||||
функция не ограничена, не имеет как наименьшего, так и наибольшего значения. Третья функция на 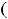

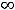
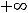
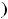 ограничена (
ограничена (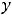
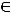
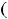

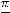
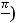
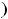 , но не имеет ни
, но не имеет ни
наименьшего, ни наибольшего значения. Её график изображён на рисунке 19. 78

Хорошо известная читателю функция |
ограничена снизу, но не |
ограничена сверху. Наименьшее значение |
принимает в точке |
локального минимума, а наибольшего значения не имеет.
График функции 5) изображён на рисунке 20. Функция ограничена;
наименьшего значения не имеет, а наибольшее значение |
|
принимает в |
||||||||||||||||||
точке |
локального максимума. |
|
|
|
|
|
|
|
|
|
|
|||||||||
График |
функции |
|
|
|
|
называется |
синусоидой |
и |
хорошо |
известен |
||||||||||
читателю. Функция ограничена |
|
|
|
|
. Наименьшее значение |
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||
принимается на бесконечном множестве точек |
|
|
|
|
|
|
, |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
являющихся точками локальных минимумов. Наибольшее значение |
|
|
|
|||||||||||||||||
достигается на бесконечном множестве точек |
|
|
|
|
, |
|||||||||||||||
|
|
|
||||||||||||||||||
являющихся точками |
локальных максимумов. При |
этом |
все |
|
|
|
||||||||||||||
|
|
|
||||||||||||||||||
(совпадает с наименьшим значением), а все |
|
|
|
(совпадают с наибольшим |
||||||||||||||||
значением). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: |
1) |
|
|
|
|
|
|
|
|
|
глобальных |
экстремумов |
нет; 4) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
=0, наибольшего значения функция не имеет; 5) |
|
, наименьшего |
||||||||||||||||||
значения нет; 6) 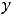


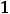
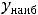

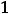
 Пример 13. Исследовать на глобальный экстремум следующие функции на
Пример 13. Исследовать на глобальный экстремум следующие функции на
указанных промежутках:
Решение. Всякая непрерывная функция, определенная на отрезке, имеет на нём как наименьшее, так и наибольшее значение. Эти значения были указаны для функций примера 11, заданных на соответствующих отрезках. Для разрывных на отрезке функций любое из этих значений могло не достигаться. Такие функции были рассмотрены в примере 10. То же может случиться и для функций, заданных на каком-нибудь из следующих промежутков: интервале 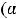
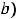 , полуотрезке [
, полуотрезке [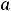
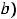 или полуотрезке (
или полуотрезке (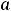
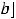 . Это может быть даже для непрерывной и ограниченной функции, заданной на таком промежутке.
. Это может быть даже для непрерывной и ограниченной функции, заданной на таком промежутке.
Отметим, что каждая функция этого примера есть сужение известных читателю функций на соответствующий промежуток, являющийся подмножеством области её определения. Их графики, на этих промежутках
79

легко построить. Кроме того, все рассмотренные функции, на указанных промежутках, непрерывны.
Линейная функция 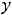

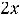
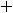
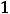 на любом из указанных промежутков является ограниченной и возрастающей. Так как на интервале (0, 1) она возрастает, но в
на любом из указанных промежутков является ограниченной и возрастающей. Так как на интервале (0, 1) она возрастает, но в
точках |
не определена, то не имеет на нём ни наименьшего, |
ни |
||
наибольшего значения. На полуотрезке [0, 1) имеем следующее: |
|
|||
; наибольшего значения нет, т.к. функция в точке |
не определена. |
На |
||
отрезке (0,1] нет наименьшего значения, а |
|
. |
|
|
Функция |
(обратная к |
) на |
указанных промежутках |
|
ограничена. На интервале (-1, 1) не имеет ни наименьшего, ни наибольшего
значения, т.к. возрастает, а в точках |
|
|
|
|
не |
определена. На |
|||||||
|
|||||||||||||
полуотрезке [-1, 1) имеем следующее: |
|
|
|
|
|
|
, наибольшего |
||||||
|
|
|
|
|
|
||||||||
значения нет. На интервале (-1, 1] нет наименьшего значения, а |
|||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Третья |
функция на заданных промежутках |
убывает, но |
|
не ограничена |
||||||||
( |
|
|
|
). На интервале (0, 2) глобальных экстремумов не имеет. На |
|||||||||
|
|
|
|||||||||||
полуотрезке (0, 2) не имеет наибольшего значения, а наименьшее значение существует и 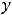

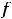
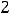

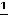 .
.
Ответы: 1) на (0,1) наименьшее и наибольшее значения не существуют; на
[0, 1) достигается наименьшее значение |
|
|
|
|
|
, а наибольшего нет; на |
||||||||
(0, 1] нет наименьшего значения, а |
|
|
|
|
; 2) на (-1,1) глобальных |
|||||||||
экстремумов нет; на [-1, 1) |
|
|
|
|
|
|
, а наибольшего значения нет; |
|||||||
|
|
|
|
|
|
|||||||||
на (-1,1] нет наименьшего значения, а |
|
|
|
|
|
|
; 3) на интервале (0,2) |
|||||||
|
|
|
|
|
|
|||||||||
наименьшего и наибольшего значений нет; на полуотрезке (0, 2] |
|
|||||||||||||
|
|
, а наибольшего значения нет. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 14. Имеется |
погонных метров металлической сетки. |
(Пусть для |
|||||||||||
примера |
). Этой сеткой надо огородить прямоугольную площадку |
|||||||||||||
наибольшей площади. Найти размеры сторон этой площадки. |
|
|||||||||||||
|
Решение. Обозначим длины сторон |
прямоугольника через |
. Тогда |
|||||||||||
площадь |
площадки |
будет равна |
. Получили функцию |
двух |
||||||||||
переменных, которую пока исследовать не умеем. Учтём, что задан периметр 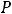
площадки. Так как |
, то имеем ещё ограничение, т.е. равенство |
. |
|
|
80 |
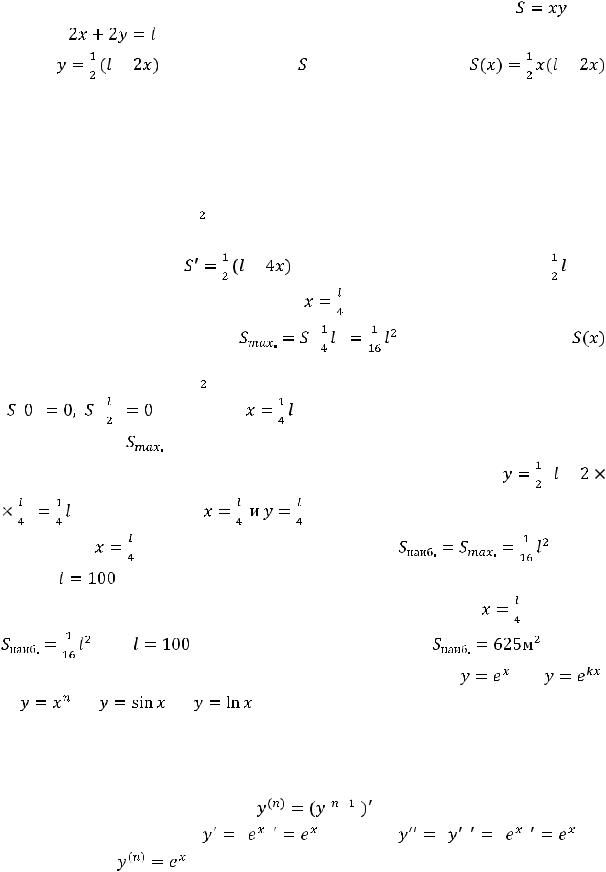
Таким |
образом, надо найти наибольшее значение функции |
|
|
|
при |
||||
условии |
|
|
|
|
, которое называют уравнением связи. Из этого уравнения |
||||
имеем |
|
|
|
|
. Тогда площадь задаётся функцией |
|
|
|
|
|
|
|
|
|
|
|
|
||
одной переменной 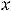 , которую надо исследовать на наибольшее значение. Очевидно, что область определения этой функции удовлетворяет неравенствам
, которую надо исследовать на наибольшее значение. Очевидно, что область определения этой функции удовлетворяет неравенствам 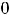
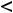
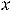
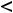
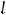 (длина стороны не может быть отрицательной и равной всему периметру, а также большей периметра; ограничение на
(длина стороны не может быть отрицательной и равной всему периметру, а также большей периметра; ограничение на 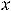 сверху можно даже уточнить, т.е. считать
сверху можно даже уточнить, т.е. считать 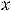
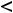
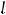 , исходя из условия
, исходя из условия 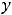
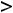
 ).
).
Далее действуем по обычной схеме исследования на глобальный экстремум.
Так как производная |
|
|
|
|
существует на интервале (0, |
|
|
), то |
||||||
|
|
|
|
|
||||||||||
критической точкой первого рода будет |
|
|
|
|
. Можно показать, что в этой точке |
|||||||||
|
|
|
|
|||||||||||
имеется максимум. При этом |
|
|
|
|
|
|
. Поскольку функция |
|
||||||
|
|
|
|
|
|
|||||||||
непрерывна на отрезке [0, 
 ] и её значения на концах этого отрезка равны нулю
] и её значения на концах этого отрезка равны нулю
( |
|
|
|
|
|
|
|
|
|
), то при |
|
|
|
|
|
функция будет иметь и |
|
наибольшее |
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
значение, равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Из уравнения связи находится другая сторона прямоугольника: |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
. Таким образом, |
|
|
|
|
|
, т.е. площадка должна быть квадратной |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
со стороной |
|
. При этом её наибольшая площадь |
|
|
|
|
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
При |
|
|
|
|
|
сторона квадрата должна быть равна 25 м. |
|
|
|
|
|
|
|
|
|
|||||||||
|
Ответ: Площадка должна быть квадратной со стороной |
|
|
, |
при этом |
||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
; при |
м сторона квадрата будет 25м, а |
|
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Пример 15. Найти производные n-го порядка функций 1) |
, 2) |
, |
||||||||||||||||||||||
3) |
|
|
, 4) |
|
|
|
, 5) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Будем находить несколько производных и затем устанавливать закономерность. Первые производные всех функций, кроме 2), имеются в таблице производных основных элементарных функций. Производная n-ого
порядка определяется равенством |
|
|
. |
|
|
|
|
||||
У первой |
функции |
. Тогда |
и, |
||
следовательно, |
. |
|
|
|
|
|
|
81 |
|
|
|

|
|
Рассмотрим вторую функцию |
|
|
. По правилу производной сложной |
|||||||||||||||||
функции |
получим |
|
. Тогда |
|
|
|
|
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
. Следовательно, |
. |
|
|
|
|
|
|
|
|
||||||
|
|
У функции |
под n подразумеваем натуральное число, а не любое |
|||||||||||||||||||
действительное число. |
Так как |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
, |
то очевидно, |
что |
|
|
|
|
|
|
|
. |
Следовательно, |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
(читается n-факториал). |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Для функции |
имеем |
следующее: |
, |
|
|
, |
||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
, |
. Четвёртая производная совпала с самой функцией. |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
Следующая совпадёт с первой и т.д., т.е. имеется некоторое повторение. Можно
понять, что при любом натуральном |
числе |
n |
справедливо равенство |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для последней |
|
|
функции |
|
|
согласно |
таблице производных имеем |
|||||||||||||||||||||||||||||||||||
следующее: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Очевидно, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
что каждая |
|
производная |
получается из |
равенства |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
(напомним, что |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответы: 1) |
; 2) |
|
|
; 3) |
|
; 4) |
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
5) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 16. Найти в данной точке |
при заданном приращении |
|
аргумента |
|||||||||||||||||||||||||||||||||||||||
дифференциалы следующих функций: 1) |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
Дифференциал |
функции |
|
|
|
определяется |
равенством |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
, при этом |
приращение |
аргумента функции |
называется |
||||||||||||||||||||||||||||||||||
дифференциалом аргумента и обозначается |
( |
|
|
. Поэтому формулу для |
||||||||||||||||||||||||||||||||||||||
дифференциала функции обычно записывают в виде |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Из выписанных формул видно, что дифференциал функции зависит как от
точки , в которой он вычисляется, так и от заданного приращения |
аргумента |
|||||
функции. Обозначения , , |
рассматриваются как единые символы. |
|
|
|||
Для первой функции имеем |
|
|
и тогда |
|
|
|
|
|
|
|
|
||
. Следовательно, |
|
|
. Последняя |
запись |
||
означает, что дифференциал этой функции, вычисленный в данной точке |
, |
|||||
|
82 |
|
|
|
|
|

зависит ещё от величины |
|
. Так как по условию |
, то |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производной функции |
|
|
является функция |
|
. |
Так как |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
то |
|
|
|
|
|
|
|
. При |
имеем, что |
||||
|
|
|
|
|
|
. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ответы: 1) |
|
; 2) |
|
|
|
|
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Пример 17. Найти приближённые значения следующих чисел: |
1) |
; |
|||||||||||||||||||||||
2) |
; 3) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. Для |
дифференцируемой функции |
справедливо |
равенство |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
есть величина более высоко порядка малости, чем |
||||||||||||
|
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Отбросив величину |
|
, получим приближённое равенство |
|
Тогда |
|||||||||||||||||||||
из определений приращения и дифференциала функции получим приближённое
равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, которое |
тем точнее, чем меньше |
||||||||||||||||||||||||||||||||
величина |
|
|
|
|
|
|
|
приращение аргумента |
функции. |
Это равенство |
|
позволяет |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
вычислить приближённое значение функции в точке |
|
|
|
|
|
|
|
близкой к точке |
, |
||||||||||||||||||||||||||||||||||||||||||
если в последней известно само значение функции и значение её производной. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Для случая 1) в качестве функции надо взять функцию |
|
|
. Так как |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
, то для данной функции приближённое равенство примет вид |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая в этом равенстве |
, |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Во втором случае за функцию берём |
|
|
|
|
|
. Так как |
, |
|
то |
||||||||||||||||||||||||||||||||||||||||
имеем приближённое равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Для вычисления |
надо в нём положить |
|
|
(что соответствует углу в |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
это число |
соответствует |
углу в |
, |
тогда |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
(радианная |
мера угла |
|
). В результате |
получим |
следующее: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83
