
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

Тестовые задания с решениями
Задание |
1. Объединением множеств |
|
и |
|
является множество… |
|
|
|
|
Варианты ответов: 1) {3,5,10}; 2) {1,3,5,7,10,12}; 3) {1,7,12}; 4) {1,12}. |
|
|||
Решение. |
Объединением множеств |
и |
называется множество |
= |
= |
, т.е. множество, состоящее из элементов обоих множеств |
|||
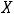 ,
, 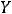 (при этом одинаковые элементы учитываются один раз). Очевидно, что в
(при этом одинаковые элементы учитываются один раз). Очевидно, что в
данном задании |
= |
. Правильным ответом является ответ 2). |
|
||
Задание |
2. |
Пересечение множеств |
и |
|
|
является множество… |
|
|
|
||
Варианты ответов: 1) {3,5,12}; 2) {1,7,12}; 3) {3,5,10}; 4) {1,3,5,7,10,12}. |
|
||||
Решение. |
Пересечение множеств |
и |
называется множество |
= |
|
|
|
, т.е. множество, состоящее из элементов, принадлежащих |
|||
как , так и |
. Общими элементами заданных множеств являются числа 3,5,10. |
||||
Следовательно, правильным ответом является ответ 3).
Задание 3. Пересечением полуотрезков [5, 15] и [1, 8) является множество…
|
Варианты ответов: 1) |
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение: Общим элементом обоих множеств являются |
числа |
, |
|||||||||||
удовлетворяющие неравенствам 5< |
. Отметим, что числа |
и |
|
|||||||||||
пересечению заданных множеств не принадлежат, поскольку |
|
не |
||||||||||||
принадлежит полуотрезку (5, 15], а |
- полуотрезку [1, 8). Таким образом, |
|||||||||||||
пересечением этих множест является интервал (5, 8). |
|
|
|
|
|
|
||||||||
|
Задание 4. Функция |
|
отражает отрезок |
на множество… |
|
|||||||||
|
Варианты ответов: 1) (0, + |
); 2) |
; 3) (0,1); |
4) [0,1]. |
|
|
|
|||||||
|
Решение. Функция |
|
определена на луче (0, +∞) и строго возрастает. |
|||||||||||
Поскольку |
и |
, то заданный отрезок отображается на ось ординат |
||||||||||||
в отрезок [0,1]. Правильным ответом является ответ 4). |
|
|
|
|
|
|
||||||||
|
Задание |
5. Областью |
|
значений |
функции |
|
|
|
|
является |
||||
|
|
|
|
|
||||||||||
множество… |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Варианты ответов: 1) (0, + |
); 2) |
; 3) ( |
|
|
); 4) [5, |
|
). |
|
|||||
|
|
|
||||||||||||
|
Решение. |
Очевидно, |
что значения этой функции увеличиваются с |
|||||||||||
увеличением |
абсолютной |
величины |
аргумента . |
Так как |
|
, |
то |
|||||||
|
||||||||||||||
|
|
|
. Следовательно, областью значений функции является |
|||||||||||
|
|
|
||||||||||||
множество 2), т.е. луч |
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
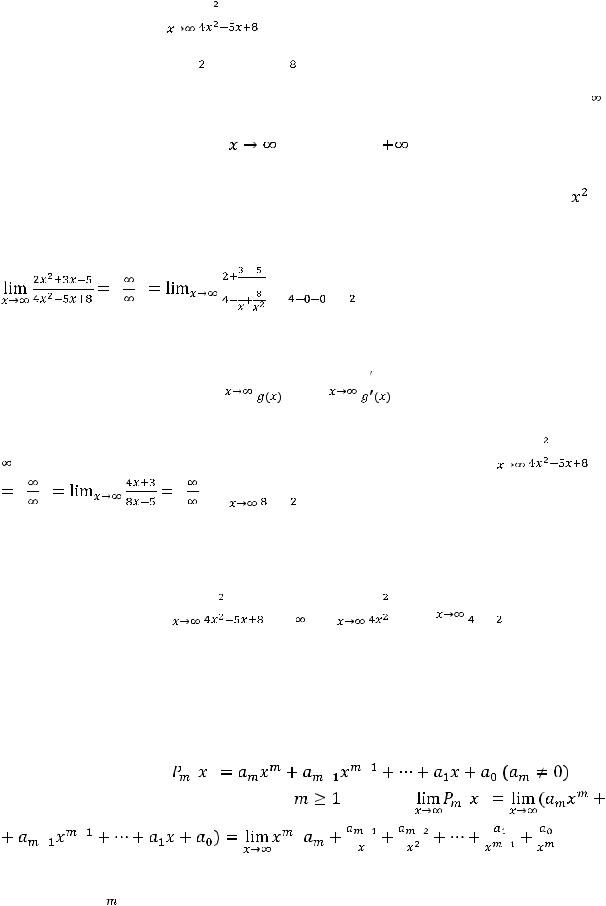
Задание 6. Предел 

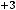


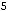 равен…
равен…
Варианты ответов: 1) 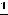 ; 2) ∞; 3)
; 2) ∞; 3) 
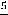 ; 4) 0.
; 4) 0.
Решение. При вычислении этого предела имеем неопределённость вида 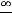 .
.
Это следует из того, что обе функции (в числители и знаменателе
рассматриваемой дроби) при |
стремятся к |
, (см., например, графики |
|
этих функций, которыми являются параболы). |
|
|
|
Для вычисления этого предела разделим числитель и знаменатель на |
и |
||
воспользуемся теоремами о пределах (предел суммы; предел частного (дроби); предел величины, обратной к бесконечно большой). В результате получим
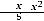


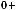


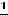 . Верным ответом является ответ
. Верным ответом является ответ
1).
Для раскрытия этой неопределённости можно применить правило Лопиталя,
которое утверждает, что 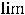
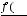
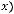

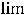

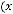
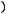 , если предел справа в этом
, если предел справа в этом
равенстве существует. Если предел справа снова представляет неопределённость
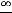 , то правило повторяют. Сказанное приводит к следующему:
, то правило повторяют. Сказанное приводит к следующему: 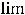

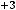


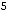


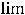
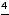

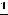 . Получен тот же результат.
. Получен тот же результат.
Ответ можно получить ещё проще. При вычислении предела отношения многочленов (полиномов) при 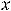
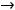
 достаточно оставить в числителе и знаменателе старшие члены (главные члены по поведению многочлена на
достаточно оставить в числителе и знаменателе старшие члены (главные члены по поведению многочлена на
бесконечности). Тогда 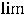

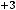


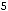

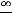

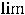
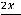

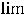
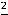

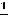 .
.
Замечание. В последнем задании в числителе стоят многочлены одинаковой (второй) степени. Применённое правило замены многочленов своими старшими членами (при вычислении на ∞ предела дробно-рациональной функции, т.е. отношения двух многочленов) можно использовать и для отношений многочленов произвольных, в том числе разных степеней. Поясним законность
этого действия. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
есть |
||||
|
|
|
|
|
||||||||||||||||||
многочлен (полином) степени |
|
. Тогда |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предел выражения квадратной скобки, очевидно, будет равен первому слагаемому 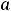 , т.к. остальные слагаемые этой скобки являются бесконечно
, т.к. остальные слагаемые этой скобки являются бесконечно
9
малыми величинами. Следовательно, |
Это |
утверждение нельзя было доказать на основании теоремы о пределе суммы, т.к. разные слагаемые многочлены могут иметь различные знаки и тогда будут возникать неопределённости вида ∞ 
 . Заметим, что значение
. Заметим, что значение 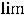
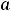
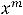 будет
будет
зависеть от знака коэффициента |
, степени |
(чётной и нечётной) и |
||||||
стремления аргумента |
к бесконечности |
|
Это правило |
|||||
|
||||||||
будет применяться в модуле 2. |
|
|
|
|||||
Задание 7. Предел |
|
|
|
|
равен… |
|
||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Варианты ответов: 1) 1; 2) 3; 3) 0; 4) 2.
Решение. Функция в точке 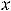

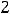 не определена, но об её пределе при
не определена, но об её пределе при 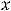
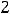 можно говорить, т.к. эта точка является предельной (точкой сгущения) для области определения функции. Подставив
можно говорить, т.к. эта точка является предельной (точкой сгущения) для области определения функции. Подставив 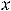

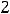 в формулу для функции, сразу установим, что имеется неопределённость вида
в формулу для функции, сразу установим, что имеется неопределённость вида 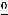 . Проще всего эта
. Проще всего эта
неопределённость раскрывается по правилу Лопиталя, которое утверждает, что
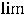
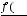
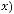

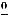

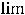

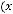
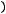 , если предел в правой части этого равенства существует. Правило повторяется, если неопределённость не раскрылась. Тогда
, если предел в правой части этого равенства существует. Правило повторяется, если неопределённость не раскрылась. Тогда
имеем |
|
|
|
|
|
|
|
|
|
|
, т.е. правильным |
|
|
ответом |
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является ответ 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример можно решить иначе. Так как имеется неопределённость |
|
|
, то это |
|||||||||||||||
|
|
|||||||||||||||||
значит, что |
является корнем уравнений |
|
|
и |
|
|
. |
|||||||||||
|
|
|
||||||||||||||||
Найдём два других корня этих квадратных уравнений. Ими являются
соответственно |
|
|
|
и |
|
|
|
|
. Тогда справедливы равенства |
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(многочлены |
разложены |
на |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
множители). Воспользовавшись |
этим, приступим к |
вычислению предела: |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Получен тот же результат. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 8. Предел 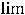
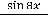 равен…
равен…
Варианты ответов: 1) 0; 2) 1; 3) 4; 4) ∞.
Решение. Так как 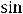
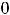

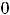 и
и 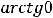

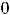 , то имеем неопределённость вида
, то имеем неопределённость вида 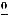 .
.
Величины 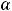

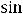
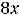 и
и 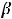

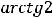
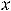 являются бесконечно малыми при
являются бесконечно малыми при 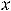
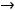
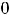 . Для вычисления исходного предела проще всего воспользоваться теоремой о замене бесконечно малых
. Для вычисления исходного предела проще всего воспользоваться теоремой о замене бесконечно малых 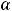 ,
, 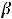 соответствующими эквивалентными им
соответствующими эквивалентными им
10

бесконечно малыми величинами 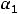 ,
, 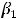 . Эта теорема утверждает, что если
. Эта теорема утверждает, что если 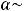
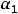 ,
,
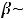
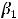 , то либо справедливо равенство
, то либо справедливо равенство 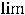
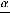

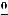

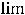
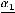 , при условии
, при условии
существования хотя бы одного из выписанных пределов, либо оба предела не
существуют. |
Известно, |
что при |
( |
, |
( |
. |
|||
Применяя |
теорему, |
получим |
|
|
|
|
|
. |
Правильным |
|
|
|
|
|
|||||
является ответ 3).
Этот предел можно найти и с помощью правила Лопиталя (см. решение
задания |
7). |
Действительно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 9. |
Правосторонний предел функции |
|
|
|
|
|
|
в точке |
|
равен… |
||||
|
|
|
|
|
|
|
||||||||
Варианты ответов: 1) 2; 2) |
; 3) 5; 4) . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Функция в точке |
не определена, однако о пределе при |
|||||||||||||
можно говорить, т.к. точка |
является предельной для области определения |
|||||||||||||
этой функции. Теоремой о пределе дроби воспользоваться нельзя из-за того, что

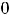 . Следовательно, имеем особый случай
. Следовательно, имеем особый случай 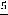 . Известно, что величина,
. Известно, что величина,
обратная к бесконечно малой, есть величина бесконечно большая (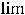
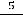

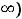 .
.
Односторонние же пределы в точке |
будут бесконечностями со знаком. |
Именно, правосторонний передел будет равен 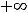 :
: 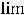
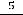

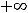 . Поясним
. Поясним
это. Функция при 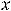
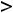
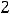 принимает положительные значения, а при
принимает положительные значения, а при 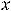
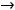
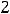 справа её значения будут увеличиваться. Действительно, при
справа её значения будут увеличиваться. Действительно, при 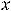

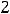
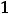 имеем
имеем 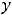

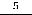

|
|
, при |
получим |
, а при |
значение функции |
||||||
|
|
||||||||||
уже равно 5000. Правильным ответом является 2). |
|
|
|||||||||
|
Задание 10. Производная функции |
равна… |
|
|
|||||||
|
Варианты ответов: 1) |
|
|
|
; 2) |
; |
|
||||
3) |
|
|
; |
4) |
|
|
. |
|
|
||
|
|
|
|
|
|||||||
|
Решение. Функция |
представляет |
собой произведение |
функций |
, |
||||||
|
|
. Производная |
произведения |
вычисляет по |
формуле |
||||||
|
|
. Так как |
, |
, |
то |
|
|||||
|
|
или |
|
, т.е ответом является 1). |
|
|
|||||
11

Задание 11. Производная функции |
|
равна… |
|
|
Варианты |
ответов: 1) |
; 2) |
; 3) |
; |
4) |
. |
|
|
|
Решение. Данная функция есть сложная функция. Точнее, она представляет
собой суперпозицию (композицию) |
трёх функций |
, |
|
, |
||||||
. Для вычисления производной её следует представить так: |
, |
|||||||||
, |
. Так |
как |
, |
|
и |
, то |
по |
правилу |
||
производной |
сложной |
функции |
получим |
|
|
|
или |
|||
|
|
|
|
, |
при |
этом |
применили |
|||
тождество |
|
|
. Правильным ответом является 4). |
|
|
|
|
|||
Задание 12. При цене |
спрос |
на товар задаётся функцией |
|
|
, |
|||||
|
||||||||||
где 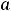 – некоторая постоянная величина. Значение показателя эластичности этой
– некоторая постоянная величина. Значение показателя эластичности этой
функции при цене |
(ден. ед.) будет равно… |
|
|
|
|
|
|
|
|||||||||||||||||
Варианты ответов: 1) |
|
2; 2) 0; |
3) |
|
8; 4) 4. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Решение. Эластичность |
функции |
определяется равенством |
|||||||||||||||||||||||
|
|
|
|
|
|
. Для данной функции |
|
|
|
|
и тогда |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
. |
При |
цене |
|
|
получим |
|
|
, т.е. ответ 3). |
|||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
Поясним экономический смысл результата: при цене |
ден. ед. повышение |
||||||||||||||||||||||||
цены товара на 1% вызовет снижение спроса на 8%. Так как |
, |
|||||||||||||
то спрос относительно цены считают эластичным. |
|
|
|
|
||||||||||
Задание 13. Производная третьего порядка функции |
|
|
равна… |
|||||||||||
|
||||||||||||||
Варианты ответов: 1) |
2) |
|
|
|
; 3) |
|
, 4) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
Решение. Вычисления можно провести по правилу нахождения производной
от дроби |
|
|
|
(на первом |
этапе |
|
|
|
|
|
). Лучше |
пользоваться равенством |
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
. Так как функцию можно записать в виде |
|
|
|
|
|
|
|
, то |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. По тому же равенству при |
|
|
имеем |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
. Тогда |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
. Правильным |
ответом |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
является ответ 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задание 14. Приближённым значением числа |
является число… |
|
|
|
|
|
|||||||||||||||||||||||||||||
Варианты ответов: 1) |
2) |
; 3) |
; 4) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. |
|
Для приращения |
|
|
функции |
|
|
и её дифференциала |
|||||||||||||||||||||||||||
справедливо приближённое равенство |
, из которого следует формула |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Это равенство тем точнее, чем меньше величина |
(приращение аргумента |
|||||||||||||||
). Для функции |
= |
эта |
формула примет |
вид |
|
|
|
|
|
|
, |
|||||
поскольку |
|
|
|
. Полагая в последнем приближённом равенстве |
||||||||||||
|
|
и учитывая, что |
|
|
|
. |
Таким образом, |
|||||||||
ответом является ответ 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Этот же результат следует из разложения функции |
а ряд Маклорена, т.е. из |
|||||||||||||||
равенства |
|
|
|
|
|
(выписанный ряд сходится для любого |
||||||||||
|
|
|
|
|
||||||||||||
действительного числа |
и своей суммой имеет |
). |
Если положить в этом |
|||||||||||||
равенстве |
|
, то ответ становится очевидным. |
|
|
|
|
|
|
|
|
|
|
||||
Задание 15. |
Область определения функции |
|
|
|
|
|
|
|
задается точками |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
плоскости, координаты которых удовлетворяют неравенству… |
|
|
||||||||||||||
Варианты |
ответов: |
1) |
2) |
|
|
|
; |
|
3) |
; |
||||||
4) 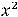
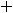
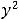
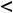
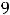 .
.
Решение. Должно выполняться неравенство 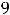

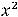

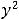
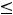
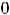 , поскольку корень извлекается из неотрицательных чисел и знаменатель дроби не может быть нулем. Это неравенство равносильно неравенству
, поскольку корень извлекается из неотрицательных чисел и знаменатель дроби не может быть нулем. Это неравенство равносильно неравенству 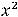
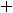
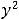
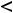
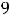 , т. е. имеет ответ 4). Геометрически это неравенство задаёт на плоскости открытый круг радиуса
, т. е. имеет ответ 4). Геометрически это неравенство задаёт на плоскости открытый круг радиуса 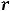

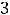 с центром в начале координат (круг без его границы – окружности
с центром в начале координат (круг без его границы – окружности
). |
|
|
|
|
|
|
|
|
|
|
|
Задание 16. Линиями уровня функции |
|
|
двух |
переменных |
|||||||
являются на плоскости кривые … |
|
|
|
|
|
|
|
|
|||
Варианты ответов: 1) |
; |
2) |
; 3) |
|
; 4) |
|
|
|
|
||
|
|
|
|
|
|||||||
Решение. |
Обычно уравнение |
|
задаёт в некотором пространстве |
||||||||
некоторую поверхность. В данном задании |
уравнение |
|
|
|
|
задаёт |
|||||
параболу, поскольку сечением в плоскости |
является парабола |
|
|
|
, а в |
||||||
плоскости |
- |
парабола |
|
. Линия уровня, |
определяемая |
|
уравнением |
||||
, является проекцией на плоскость |
всех точек |
пересечения |
|||||||||
поверхности |
с |
плоскостью |
( – |
некоторое |
постоянное |
число), |
|||||
перпендикулярной оси |
(параллельной координатной |
плоскости |
). В |
||||||||
каждой точке |
|
линии уровня функция принимает постоянное значение . |
|||||||||
Термин «линия уровня» заимствован из картографии. В экономике линию уровня называют кривой безразличия, поскольку безразлично, какую взять точку
на этой линии, чтобы получить одно и то же значение функции |
. |
13 |
|

Придавая числу |
различные значения |
(однако такие, чтобы имело место |
пересечение поверхности с плоскостью |
), будем получать различные линии |
|
уровня. Очевидно, что линии уровня заданной функции определяются уравнением 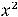
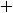
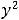

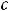 , причём
, причём 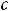
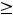
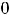 . При
. При 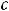
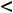
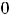 плоскость
плоскость 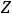

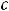 не будет пересекать параболу. Таким образом, линиями уровня рассматриваемой
не будет пересекать параболу. Таким образом, линиями уровня рассматриваемой
функции являются концентрические окружности радиуса |
|
|
. |
|
При |
|
|||||||||||||||||||||||||||||||
уравнение |
задаёт одну точку (0,0), которую называют вырожденной |
||||||||||||||||||||||||||||||||||||
линией уровня. В этой точке функция имеет |
|
наименьшее |
|
значение |
. |
||||||||||||||||||||||||||||||||
Правильным ответом является 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Задание 17. Частная производная |
|
функции |
|
|
|
|
|
|
|
равна… |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Варианты ответов: |
1) |
|
|
|
|
|
; |
2) |
|
|
; |
3) |
|
|
|
|
|
|
|
; |
4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Функция является сложной. Она представима в виде |
, где |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
есть функция двух переменных |
|
. При вычислении частной |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
производной функции |
|
|
по переменной |
величину |
считают постоянной. |
||||||||||||||||||||||||||||||||
Тогда |
|
. Очевидно, |
что |
|
|
|
|
|
|
. По правилу |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Верным является ответ 1). |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Задание 18. Стационарной точкой функции |
|
|
|
|
|
|
|
|
|
|
|
|
является… |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Варианты ответов: 1) |
2) |
|
|
|
3) |
|
; 4) |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Решение. Стационарными точками дифференцируемой функции двух переменных называются точки, в которых обе частные производные обращаются
в нуль ( |
. Таким образом, эти точки находятся как решения системы |
||||||||||
уравнений |
|
. Очевидно, что в случае заданной функции |
|
|
|||||||
|
|
|
|||||||||
|
|
. |
Тогда |
система уравнений |
|
|
, |
|
|
имеет |
|
|
|
|
|||||||||
единственное |
решение |
Стационарной |
точкой этой |
функции |
|||||||
является точка (2,1), т.е. имеем ответ 3). В модуле 4 выясним наличие экстремума в этой точке.
Задание 19. Неопределённый интеграл от функции |
|
|
|
|
|
|
|
равен… |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Варианты ответов: 1) |
; 2) |
; 3) |
|
; 4) |
|||||
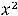
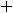
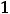
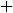
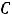 .
.
Решение. |
есть некоторая первообразная функции |
, |
|
то |
|
где C – произвольное постоянное число. Тогда будет |
|
выполняться |
равенство |
, по которому |
проверяется |
|
|
14 |
|

справедливость ответа. В данном задании имеем |
|
|
|
|
|
|
|
|
, так |
||||||||||
|
|
|
|||||||||||||||||
|
|
||||||||||||||||||
как производная правой части совпадает с подынтегральной функцией |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
. |
Действительно, ( |
|
|
|
|
|
|
|
|
|
. Правильным |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
ответом является 4). |
|
|
|
|
|
|
|
||||||||||||
|
Этот |
интеграл можно найти методом замены |
переменной (методом |
||||||||||||||||
подстановки). |
Положим |
|
|
|
|
|
|
, |
|
|
тогда |
|
|
|
, а |
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. При этом |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
воспользовались табличным интегралом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Задание |
20. |
|
|
|
|
Площадь |
|
фигуры, |
|
ограниченной |
кривыми, |
заданными |
||||||||||||||||||||||||||
управлениями |
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
, равна… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Варианты ответов: 1) |
2) |
|
|
|
; 3) |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Решение. Площадь S фигуры, ограниченной графиками непрерывных |
||||||||||||||||||||||||||||||||||||||
функций |
|
|
|
|
|
и |
, |
|
вычисляется по |
|
формуле |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
При этом предполагается: кривые пересекаются только в двух точках; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
есть проекции точек пересечения кривых на ось |
и |
; |
|
|
|
|
|
|
на |
|||||||||||||||||||||||||||||||
отрезке |
, |
т.е. |
график функции |
|
|
на этом отрезке расположен выше |
||||||||||||||||||||||||||||||||||
графика функции |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В данном задании прежде всего надо уравнения разрешить относительно переменной 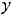 , т.е. получить виды функций. Первое уравнение (алгебраическое уравнение второй степени) приводится к виду
, т.е. получить виды функций. Первое уравнение (алгебраическое уравнение второй степени) приводится к виду 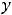

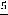 . Оно задаёт равностороннюю гиперболу, асимптотами которой являются оси координат, с
. Оно задаёт равностороннюю гиперболу, асимптотами которой являются оси координат, с
ветвями, расположенными |
в первой и третьей четвертях. |
Второе |
уравнение |
||
(алгебраическое уравнение |
первой степени) приводится к |
виду |
|
|
и |
|
|
||||
задаёт на плоскости прямую линию. Читателю рекомендуем построить графики этих кривых.
Теперь надо найти точки пересечения кривых (это поможет и построению их графиков). Для этого надо решить систему уравнений
15

Координаты этих точек практически очевидны: |
|
|
|
|
|
. Если |
||||||
читателю это не очевидно, то надо решать уравнение |
|
|
|
|
или |
|
|
|
. |
|||
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||
Тогда |
|
|
и, следовательно, |
|
|
(надо |
применить |
|||||
|
|
|
||||||||||
формулу нахождения |
корней квадратного уравнения |
или теорему Виета). |
||||||||||
Подставляя корни |
|
|
|
|
|
|
|
|
в любое уравнение системы, |
|
|
найдём |
||||||||||||||||||||
соответствующие ординаты точек пересечения кривых: |
|
|
|
|
|
.Числа |
||||||||||||||||||||||||||
|
|
|
есть проекции |
точек |
на ось |
|
абсцисс. |
Они |
являются |
|||||||||||||||||||||||
пределами интегрирования при вычислении площади |
по указанной формуле. |
|||||||||||||||||||||||||||||||
Так как на отрезке |
выполняется неравенство |
|
|
|
|
|
|
|
, |
то за |
|
|
надо |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
взять функцию |
|
, а |
|
за |
– функцию |
|
|
|
|
. Тогда |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. правильным ответом является 4). При вычислении интеграла была применена основная формула интегрального исчисления – формула Ньютона-
Лейбница |
|
|
, где |
есть первообразная |
|
||||
непрерывной подынтегральной функции |
, а также таблица первообразных |
|||
основных элементарных функций. |
|
|
||
Просматривая варианты ответов, можно |
было бы |
сразу остановиться на |
||
четвёртом ответе. Действительно, первое уравнение приводится к виду |
|
|
|
|
и, |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
следовательно, в интеграле для вычисления |
должна присутствовать функция |
|
, |
||||||||||||||||||||
|
|||||||||||||||||||||||
первообразной которой |
является |
функция |
|
|
. В |
первых трёх |
|
ответах |
|||||||||||||||
натуральный логарифм какого-нибудь числа не участвует. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задание 21. Значение |
|
|
|
|
|
равно… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Варианты ответов: 1) |
|
|
2) |
3) 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Так как первообразной функции |
|
|
является |
функция |
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
(действительно, |
|
|
), то |
по приведённой при |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
решении задания 20 формуле Ньютона-Лейбница получим |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||

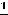
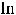
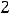 .
.
Ответом является 1).
16

Задание 22. Значение несобственного интеграла |
|
|
|
|
|
равно… |
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
Варианты ответов: 1) 0; 2) + ; 3) 1 |
4) -1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
Отметим, |
что подынтегральная функция |
|
|
|
|
|
|
|
|
|
непрерывна на |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
промежутке интегрирования |
|
. Вычисление интеграла можно было бы |
|||||||||||||||||||||||||||
провести |
по |
определению |
такого |
несобственного |
|
|
интеграла, |
т.е. по |
|||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
( |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычисление же |
|
(в данном случае интеграла |
|
|
|
|
|
|
|
|
) провести по |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
формуле Ньютона-Лейбница. Предоставляем это читателю. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Проще |
воспользоваться |
обобщённой |
|
|
|
формулой |
|
|
|
Ньютона-Лейбница: |
|||||||||||||||||||
|
|
|
|
, |
|
где |
– |
|
первообразная |
функции |
и |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
. |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Здесь |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
применена условная запись |
|
|
(величина, обратная к бесконечно большой. |
||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Есть величина бесконечно малая). Получили ответ 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Задание 23. Решением дифференциального уравнения |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
является функция… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Варианты ответов: 1) |
|
|
|
; |
2) |
|
|
|
|
|
; |
3) |
; |
|
|||||||||||||||
4) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. После подстановки функции и её производных в уравнение должно получиться тождество. Тогда ясно, что ответы 1), 3) и 4) отпадают. Например,
функция |
|
|
|
является многочленом, её производные также будут |
||||||||||||||||
многочленами |
( |
|
|
|
|
, |
а справа |
в уравнении |
стоит |
|||||||||||
тригонометрическая функция |
|
. Надо проверять функцию |
. |
|||||||||||||||||
Подставив эту функцию и её |
производные |
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
в данное уравнение, действительно получим тождество: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Решением |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дифференциального уравнения является функция из ответа 2). |
|
|
|
|
|
|
||||||||||||||
|
|
Задание 24. Общим решением дифференциального уравнения |
|
|
|
|||||||||||||||
|
|
|
|
|
|
является функция… |
|
|
|
|
|
|
|
|
|
|||||
|
|
Варианты ответов: |
1) |
|
|
; 2) |
; |
3) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
; 4) |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Решение. |
Уравнение является линейным однородным дифференциальным |
|||||||||||||||||
уравнением |
второго |
порядка с |
постоянными |
коэффициентами. |
|
|
Его |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|

характеристическое (вековое) уравнение имеет вид |
. |
Корнями |
|||||||||||||||
этого уравнения являются действительные числа |
|
|
|
|
|
. |
Так как |
||||||||||
|
|
||||||||||||||||
корни различны, то фундаментальная система решений состоит из |
функций |
||||||||||||||||
|
|
, |
|
|
. Общим решением будет функция |
|
|
|
|
|
|
|
, где |
||||
|
|
|
|
|
|
|
|
||||||||||
– производные постоянные. Имеем ответ 4). |
|
|
|
|
|
|
|
|
|||||||||
Задание 25. Решением задачи Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
является функция… |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Варианты |
ответов: 1) |
2) |
|
|
3) |
|
|
|
|
|
|
|
|||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
Искомая функция |
|
должна удовлетворять |
|
самому |
||||||||||
дифференциальному уравнению и должны выполняться |
начальные |
условия |
|||||||||||||||
|
|
|
|
|
. Если один из предложенных ответов является верным, то |
||||||||||||
достаточно проверить для рассматриваемой функции выполнение этих условий.
Первое из этих равенств |
выполняется для функции из ответов 1) и 3). |
|
Ответы 2) и 4) отпадают. Второе равенство |
для функции |
|
(первый вариант ответа) не выполняется, т.к. |
и тогда |
|

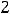 . Таким образом, остаётся ответ 3). Предоставляем читателю проверить, что для функции ответа 3) равенство
. Таким образом, остаётся ответ 3). Предоставляем читателю проверить, что для функции ответа 3) равенство 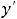
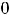

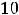 выполняется.
выполняется.
Теперь приведём подробное решение этого задания. Сначала надо найти
общее решение уравнения |
|
|
|
. Его |
характеристическим |
|||||
|
|
|
||||||||
уравнением является алгебраическое |
равнение |
|
|
или |
|
|
||||
|
|
|||||||||
|
, корень которого |
является двукратным. Тогда фундаментальная |
||||||||
|
||||||||||
система решений этого уравнения состоит из функций |
, а его |
|||||||||
общим решением является функция |
, где |
– производные |
||||||||
постоянные. Если ищется частное решение т.е. решение, удовлетворяющее
заданным |
начальным условиям |
(в |
данном |
случае |
условием |
|||
|
), |
то |
будут конкретными действительными числами. Эти числа |
|||||
находятся из |
вида общего решения и этих условий. Так как |
|
||||||
, а по первому начальному условию |
, |
то получим первое |
||||||
равенство |
|
. |
Теперь находим |
|
|
|
||
|
|
|
|
|
. Тогда |
|
|
, а по второму |
начальному |
условию |
. |
Получим второе равенство |
. |
||||
Таким образом, |
есть решения системы , |
|
|
из двух |
||||
линейных |
алгебраических уравнений |
с двумя |
неизвестными |
. Решение |
||||
|
|
|
|
|
18 |
|
|
|
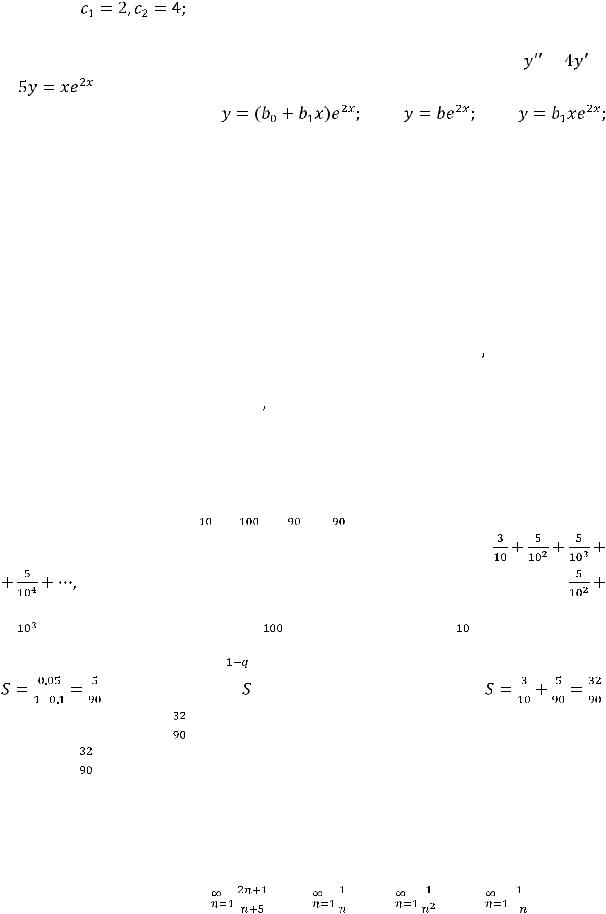
очевидно: |
при этом оно единственное. Подставляя эти значения в |
|||||||
форму общего решения, получим ответ 3). |
|
|
|
|
|
|
||
|
Задание 26. Частное решение дифференциального уравнения |
|
|
|
|
|||
|
|
|||||||
|
имеет вид… |
1) |
2) |
3) |
|
|
|
|
|
|
|
|
|
||||
|
Варианты ответов: |
|
|
|
|
|||
4) 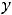

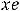
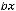

Решение. Уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами и правой частью 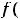
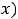 вида
вида 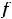
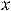

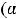

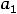
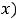
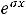 , при этом в данном задании контрольное число
, при этом в данном задании контрольное число 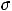

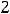 . Вид частного решения зависит от вида
. Вид частного решения зависит от вида 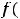
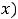 и от связи контрольного числа
и от связи контрольного числа 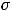 с корнями характеристического уравнения соответствующего приведённого однородного дифференциального уравнения, которое в данном задании имеет вид
с корнями характеристического уравнения соответствующего приведённого однородного дифференциального уравнения, которое в данном задании имеет вид 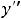

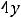


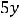

 . Тогда характеристическое уравнение таково:
. Тогда характеристическое уравнение таково: 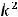

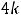

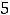

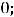 его корнями являются числа
его корнями являются числа 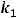


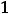
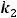

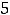
 Так как
Так как 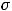

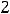 не совпадает ни с одним из корней, то частное решение надо искать в виде
не совпадает ни с одним из корней, то частное решение надо искать в виде 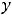

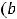

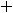
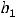
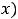
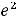
 . Числа
. Числа 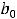
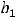 подлежат нахождению. Таким образом, частное решение надо искать в виде 1).
подлежат нахождению. Таким образом, частное решение надо искать в виде 1).
Задание 27. Бесконечная десятичная периодическая дробь 0,3(5) представляется обыкновенной дробью в виде…
Варианты ответов: 1) 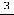
 2)
2)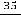 ; 3)
; 3) 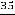
 4)
4) 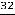

Решение. Число 0,3(5)=0,3555… записывается в виде ряда
отбросив первый член которого получим геометрический ряд
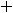
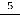
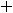
 с первым членом
с первым членом 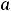

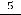 и знаменателем
и знаменателем 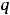

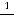 , сумма которого вычисляется по формуле
, сумма которого вычисляется по формуле 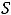

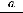 . В данном случае сумма геометрического ряда
. В данном случае сумма геометрического ряда
|
|
|
|
|
|
|
|
и тогда сумма исходного ряда есть число |
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, 0,3(5)= |
|
, т.е. правильным ответом является 4). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
Число |
|
|
|
специально не сокращали, чтобы читатель мог понять |
правило |
||||||||||||
|
|
|
|||||||||||||||
перевода бесконечных десятичных периодических дробей в обыкновенные дроби. Другие типы примеров будут приведены в модуле 7.
Задание 28. Из данных в вариантах ответов числовых рядов сходящимся является ряд…
Варианты ответов: 1) |
|
; 2) |
19 |
|
; 3) |
|
; 4) |
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|

Решение. Сходящимся рядом является только ряд 3). Общий член |
первого |
||||
ряда |
|
не стремится к нулю ( |
|
|
. Он |
|
|
||||
является расходящимся, поскольку не выполнено необходимое условие сходимости числового ряда, т.е. условие 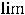
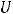

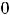 . Второй ряд называется гармоническим; известно, что он расходится, хотя необходимое условие
. Второй ряд называется гармоническим; известно, что он расходится, хотя необходимое условие
сходимости |
|
|
выполнено. Третий и четвёртый ряды |
||
|
|
||||
относятся к обобщённому гармоническому ряду |
|
. Известно, что ряды |
|||
|
|||||
такого вида сходятся при |
(таким является ряд 3)) и расходятся при |
||||
(таким является ряд 4)). |
|
|
|
|
|
Докажем сходимость ряда 3) с помощью интегрального признака Маклорена-
Коши. Этот признак утверждает следующее: если функция |
на промежутке |
|||||
непрерывна, неотрицательна, не возрастает и |
|
, то |
||||
положительный числовой ряд |
и несобственный интеграл |
|
|
|
||
одновременно сходятся или расходятся. |
|
|
|
|
|
|
Очевидно, что в этом примере в качестве |
надо взять функцию |
|
|
, |
||
|
||||||
которая всем условиям сформулированной теоремы удовлетворяют. Вычислим соответствующий интеграл: 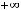
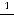
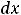


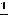


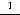

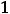

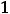 . Так как
. Так как
он сходится, то сходится и ряд 3). Специальными методами устанавливается, что сумма этого ряда равна 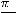 .
.
Расходимость рядов 2) и 4) можно доказать с помощью этого же признака (см. примеры модуля 7). Расходимость ряда 4) можно установить и с помощью признака сравнения, так как при 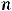
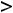
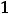 выполняется неравенство
выполняется неравенство 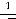
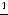 , то его
, то его
сравниваем с гармоническим рядом.
Сходимость ряда 3) можно доказать и с помощью признака сравнения. Для
этого его можно сравнить со сходящимся |
рядом |
|
. Читателю |
||||||||
|
|||||||||||
предлагаем установить, что частичная сумма |
этого последнего ряда равна |
||||||||||
|
|
|
|
. В соответствии с определением суммы |
ряда получим |
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
20

Задание 29. Областью |
сходимости |
степенного |
ряда |
|
|
является |
|||
|
|
||||||||
промежуток… |
|
|
|
|
|
|
|
||
Варианты ответов: 1) |
|
|
; 2) |
|
; 3) |
; 4) |
(-1,1). |
|
|
|
|
|
|
||||||
Решение. Исследуемый ряд является степенным. |
Для нахождения области |
||||||||
сходимости можно было бы применить предельный признак Даламбера к ряду
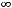
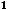
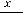 , составленному из абсолютных величин членов исходного ряда.
, составленному из абсолютных величин членов исходного ряда.
Обычно область сходимости устанавливают так. Сначала находят число 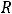 -
-
радиус сходимости степенного ряда. Если |
|
|
есть конечное число, |
не равное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нулю, то ряд будет сходиться на интервале |
|
|
|
, а вне этого интервала будет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
расходиться. Остаётся провести исследование на сходимость в точках |
|
|
|
|
|
|
|
|
, т.е. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
на концах интервала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Радиус сходимости |
|
можно найти по формуле |
|
, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
есть коэффициент при , т.е. коэффициент общего члена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Эта |
||||||||||||||||||||||||||||||||||||||||||||||
формула очень удобна в данном задании. Так как |
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
, то |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Тогда ряд |
сходится |
на |
интервале |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(-1,1). Теперь проверим его сходимость в точках |
|
|
|
|
и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
При |
|
|
|
|
|
|
|
|
получим числовой знакочередующийся ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Очевидно, что его члены убывают по абсолютной величине и |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
предел общего члена |
|
|
|
|
|
равен нулю; это значит, что ряд является рядом типа |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и, следовательно, сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
При |
|
|
|
|
|
|
имеем положительный числовой ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
сходимость которого установлена в предыдущем задании. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Из всего сказанного следует, что ряд сходится на отрезке |
|
|
|
|
, |
|
т.е. имеем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ответ 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Задание 30. Член ряда Маклорена функции |
|
|
|
|
|
|
|
|
, |
|
|
содержащий |
|||||||||||||||||||||||||||||||||||||||||||||||||||
четвёртую степень переменной |
, имеет вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Варианты ответов: 1) |
|
|
2) |
|
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Решение. Степенной ряд вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
называется рядом Маклорена функции |
|
|
. Для функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеем |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а |
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
