
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

Если выписанный предел существует и конечен, то интеграл называют сходящимся, а в противном случае – расходящимся.
Приступим к исследованию данных интегралов, т.к. они являются интегралами описанного типа, т.е. функция имеет особенности только на левых концах соответствующих промежутков.

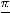 , т.е.
, т.е.
первый интеграл сходится и равен 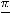 .
.


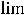
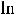
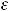

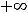 , т.е. этот
, т.е. этот
интеграл расходится.
Ответы: 1) 
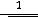
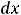

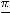 (сходится); 2) интеграл расходится.
(сходится); 2) интеграл расходится.
Замечание. Имеются ещё несобственные интегралы второго рода с конечным промежутком 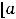
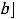 интегрирования и особенностью во внутренней точке с этого промежутка
интегрирования и особенностью во внутренней точке с этого промежутка 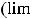
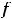
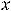

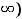 . Если эта точка единственная, то интеграл
. Если эта точка единственная, то интеграл
определяется равенством 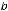
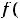
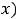
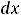


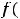
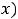
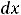
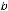
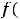
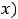
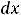 . Интегралы, стоящие справа в этом равенстве, уже рассмотрены в предыдущих примерах 9 и 10; один из них имеет особенность на правом конце, а другой – на левом.
. Интегралы, стоящие справа в этом равенстве, уже рассмотрены в предыдущих примерах 9 и 10; один из них имеет особенность на правом конце, а другой – на левом.
Модуль 6. Дифференциальные уравнения
Пример 1. |
Указать тип уравнения |
|
|
|
и проверить, является ли |
|
|
|
|||
функция |
его решением. |
|
|
|
|
Решение. Уравнение относится к обыкновенным дифференциальным уравнениям второго порядка, поскольку неизвестная функция 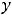

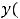
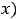 является функцией одной переменной и производной высшего порядка, входящей в
является функцией одной переменной и производной высшего порядка, входящей в
уравнение, является производная второго порядка. |
|
Решением дифференциального уравнения называется |
такая функция |
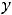

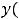
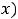 , которая при подставке в уравнение вместе с содержащимися в нем её производными обратит уравнение в тождество. Отметим, что сама функция и её производные некоторого порядка, кроме высшего, могут явно в уравнении не присутствовать.
, которая при подставке в уравнение вместе с содержащимися в нем её производными обратит уравнение в тождество. Отметим, что сама функция и её производные некоторого порядка, кроме высшего, могут явно в уравнении не присутствовать.
101

Подставив |
|
, в данное уравнение, |
получим тождество |
. Следовательно, функция |
является одним из |
решений этого уравнения. |
|
|
Ответ: Уравнение является обыкновенным дифференциальным уравнением
второго порядка, а функция |
|
является одним из его решений. |
|
||
Пример 2. Выяснить, является ли функция |
решением |
||||
дифференциального уравнения |
|
|
|
. |
|
|
|
|
|||
Решение: Уравнение относится к дифференциальным уравнениям второго порядка в частных производных. Очевидно, что частные производные первого порядка таковы: 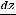

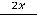
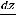

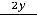 .
.
Вычислим теперь входящие в уравнение частные производные второго порядка:
,
.
Очевидно, что при их подстановке в уравнение получится тождество.
Ответ: Функция является решением данного дифференциального уравнения
в частных производных. |
|
|
|
|
|
|
|||||||
|
Пример 3. Найти решения дифференциальных уравнений |
1) |
|
|
; |
||||||||
|
|
||||||||||||
2) |
|
|
|
|
; 3) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решение: Запись дифференциального |
уравнения первого |
порядка в |
виде |
|||||||||
|
|
|
|
|
|
|
|
называется дифференциальной формой. |
Если |
эта |
|||
форма |
примет вид |
, |
то дифференциальное |
уравнение |
|||||||||
называют уравнением с разделенными переменными. Проинтегрировав последнее равенство, получим общее решение такого уравнения в виде интегралов (квадратур) 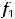
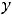
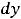

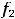
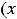
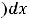 .
.
Если интегралы выражаются через элементарные функции, то получим решение 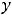

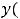
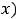 , в явном или неявном виде.
, в явном или неявном виде.
Во всех заданных уравнениях переменные разделены. В результате
интегрирования получим следующие результаты: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
; |
|
||||||||
|
|
|
|||||||||||
102 |
|
||||||||||||

. |
|
Общее решение первого уравнения получилось в неявном виде |
. |
Семейством интегральных кривых является множество концентрических
окружностей с центром в начале координат радиуса |
. В явном виде решения |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
задаются полуокружностями |
|
|
и |
|
|
|
|
. |
||
|
|
|
||||||||
Интегральными кривыми второго уравнения являются прямые линии
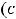
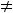
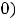 .
.
Решение последнего уравнения записано в квадратурах, выписанные
интегралы не выражаются через элементарные функции. |
|
||||||
Ответы: 1) |
; 2) |
; 3) |
|
|
. |
||
|
|
||||||
Пример 4. |
Найти общие |
решения дифференциальных уравнений |
|||||
1) |
|
|
; 2) |
. |
|
|
|
|
|
|
|
|
|||
Решение: |
Если дифференциальная форма имеет |
вид |
|||||
|
|
|
, то дифференциальное уравнение называется уравнением с |
||||
разделяющимися переменными. |
Делением на |
оно приводится к |
|||||
уравнению с разделёнными переменными, общий интеграл которого в квадратурах имеет вид 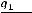
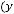
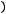
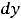

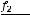
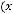
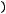
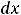 .
.
Отметим, что при делении возможна потеря частных решений.
Оба уравнения относятся к уравнениям с разделяющимися переменными.
Разделив первое уравнение на |
|
|
|
, получим уравнение |
|
|
|
с |
||||||||||
|
|
|
||||||||||||||||
разделёнными переменными. Интегрируя его, получим |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
или |
|
|
|
|
|
. Тогда |
|
|
|
. При делении на |
потеряли |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
||||||||||||||||||
очевидное решение |
. Это решение можно учесть предыдущим равенством, |
|||||||||||||||||
если в нём положить |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Окончательно имеем, что общее решение первого уравнения можно записать
в виде |
|
|
, где – любое постоянное число. |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
Второе уравнение также разделим на |
. Получим уравнение |
с |
||||||||||
разделёнными переменными |
|
|
. Интегрируем его, |
при этом интеграл |
||||||||
|
||||||||||||
от функции |
|
|
|
|
берется подстановкой |
. |
Получим |
|
||||
|
|
|
|
|
||||||||
|
|
|
|
или |
. |
При делении на |
потеряли |
|||||
решение |
|
|
, которое исходному |
уравнению |
удовлетворяет. |
Итак, |
= |
|||||
|
|
|
|
|
|
|
|
103 |
|
|
|
|


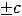
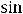
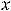
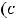
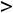
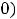 и
и 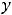

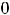 , тогда общее решение есть функция
, тогда общее решение есть функция 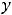

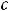
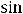
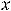 , где
, где
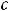 – произвольная постоянная.
– произвольная постоянная.
Ответы: 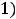

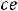

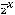

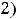
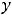

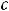
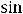
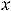

Пример 5. Найти общее решение линейного дифференциального уравнения
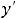

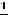
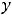

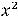 .
.
Решение. Решим соответствующее линейное приведённое однородное
уравнение |
|
|
|
|
|
. Разделив переменные в последнем уравнении, получаем |
|||
|
|
|
|
||||||
уравнение |
|
|
|
|
|
|
|
, интегрируя которые имеем |
или |
|
|
|
|
|
|
||||
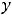

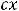 ; где
; где 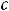
 любая постоянная ( случай
любая постоянная ( случай 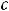

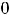 учитывает потерянное решение
учитывает потерянное решение
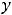
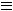
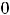 ).
).
Итак, 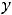

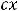 есть решение приведённого однородного уравнения. Решение исходного уравнения получим так называемым методом вариации произвольной постоянной. В записи
есть решение приведённого однородного уравнения. Решение исходного уравнения получим так называемым методом вариации произвольной постоянной. В записи 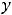

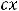 будем считать
будем считать 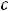 функцией переменной
функцией переменной 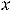 , т.е. решение исходного уравнения будем находить в виде
, т.е. решение исходного уравнения будем находить в виде
Метод получил название в связи с тем, что постоянную варьируем (изменяем). По существу совершается замена переменной 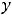

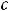
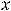
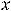 , где
, где 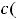
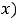 – новая неизвестная функция.
– новая неизвестная функция.
Теперь функцию (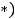 и её производную
и её производную 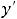

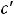
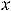
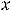
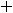
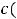
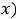 подставляем в исходное уравнение. После очевидного упрощения имеем уравнение
подставляем в исходное уравнение. После очевидного упрощения имеем уравнение 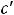
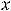
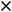
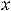

|
|
или |
. |
|
Тогда |
|
|
, где |
– любая |
постоянная, не |
|
||||||||||
зависящая от |
. Подставив найденную функцию |
в ( , получим |
||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Очевидно, |
что |
|
есть частное |
решение |
исходного |
неоднородного |
|||
|
|
|||||||||
уравнения, получающееся из его общего решения при 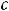

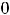 .
.
Ответ: 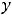

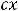
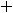
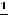
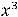 .
.
Пример 6. Найти решение задачи Коши 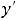

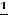
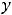

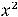
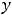
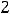

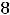 .
.
Решение. Решение задачи Коши (задачи с начальным условием) есть решение дифференциального уравнения, удовлетворяющее заданному начальному условию. В данном примере этим условием является 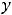
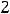

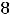 . Такое решение называется частным решением дифференциального уравнения.
. Такое решение называется частным решением дифференциального уравнения.
104

Геометрически это трактуется так: из всего семейства интегральных кривых (из общего решения) надо выделить интегральную кривую, проходящую через заданную точку 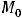
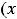

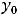
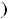 .
.
Частное решение дифференциального уравнения находится из его общего решения путём подбора соответствующей постоянной 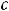 .
.
Общее решение данного уравнения уже найдено в примере 5. Из его вида
|
|
найдём |
|
|
|
|
. С другой стороны, по |
||
|
|
|
|
||||||
условию дано |
. Тогда |
|
и, следовательно, |
. Итак, |
|||||
частным решением является функция |
|
|
. |
|
|||||
|
|
||||||||
Ответ: |
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
||||
Пример 7. Найти общие решения следующих дифференциальных уравнений:
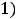
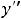

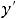

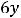

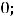
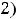
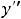

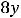

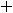
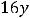

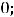
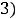
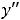
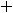
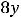

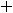
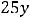

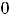 .
.
Решение. Все уравнения примера являются линейными однородными дифференциальными уравнениями второго порядка с постоянными
коэффициентами. |
|
Пусть функции |
линейно независимы |
являются решениями линейного однородного уравнения второго порядка
Тогда говорят, что они образуют фундаментальную систему решений этого уравнения. В таком случае выражение 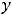

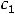
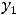
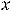
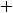
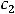
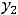
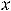 где
где 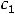
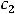 – произвольные постоянные, содержит все решения этого уравнения (особых решений нет). Таким образом, общее решение линейного однородного уравнения второго порядка есть линейная комбинация функций, образующих его фундаментальную систему решений.
– произвольные постоянные, содержит все решения этого уравнения (особых решений нет). Таким образом, общее решение линейного однородного уравнения второго порядка есть линейная комбинация функций, образующих его фундаментальную систему решений.
Фундаментальная система решений уравнения 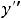
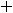

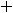
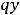

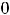 с постоянными коэффициентами связана с корнями его характеристического
с постоянными коэффициентами связана с корнями его характеристического
уравнения |
|
|
|
|
Справедливы следующие утверждения: |
|
|
|
Если корни |
характеристического уравнения действительны и различны |
|
( |
, то фундаментальную систему образуют функции |
. |
|
|
Если характеристическое уравнение имеет один корень |
кратности 2, то |
|
Если корни комплексны (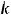

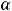
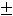
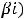 то
то 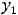

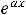
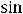
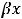

105

Характеристическим уравнением первого дифференциального уравнения
является алгебраическое уравнение |
|
|
|
|
|
. Его корни таковы: |
|||||||||
|
|
||||||||||||||
|
|
. Функции |
|
|
|
|
образуют |
фундаментальную |
|||||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
систему решений этого уравнения. Действительно, |
|
|
и легко проверить, |
||||||||||||
|
|
||||||||||||||
что каждая функция является решением этого уравнения. Функция |
|
|
|||||||||||||
|
|||||||||||||||
|
|
есть общее решение уравнения 1). |
|
|
|
|
|
||||||||
Алгебраическое уравнение |
|
|
|
есть |
характеристическое |
||||||||||
|
|
||||||||||||||
уравнение для дифференциального уравнения |
2). Оно имеет только один корень |
|
(кратности 2). Для 2) фундаментальную систему решений образуют |
||
функции |
(проверьте это); |
общее решение имеет вид |
В случае 3) имеем 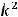
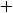
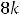
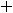
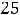

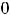
 Тогда
Тогда 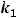
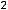

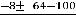

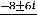


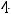
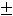
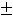
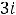 , т.е. имеем пару комплексно сопряжённых корней. Фундаментальную систему решений составляют функции
, т.е. имеем пару комплексно сопряжённых корней. Фундаментальную систему решений составляют функции 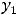

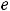

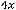
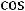
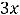
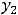

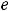

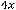
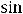
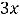 , а общее решение
, а общее решение 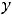

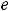

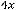
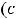
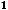
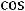
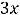
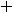
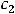
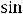
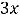
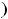

Ответы:
Пример 8. Найти решения дифференциального уравнения 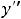

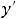

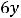

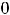 , удовлетворяющее начальным условием
, удовлетворяющее начальным условием 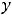
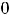

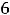
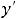
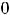

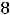

Решение. Речь идёт о задаче Коши или задаче с начальными условиями для данного дифференциального уравнения. Это значит, что из всего множества решений (из общего решения) надо выбрать ту функцию, которая удовлетворяет заданным начальным условиям. Эта функция есть частное решение этого дифференциального уравнения.
Общее решение данного уравнения найдено в задании 1) примера 7. Оно
имеет вид |
|
|
|
|
|
. Постоянные |
найдутся из заданных |
||||||
|
|
|
|
|
|||||||||
начальных условий. |
|
|
|
|
|
|
|||||||
Вычислим |
при |
|
|
|
|
. С другой стороны, |
|||||||
по условию примера |
. Тогда имеем равенство |
. |
|||||||||||
Так как |
|
|
|
|
|
|
|
, то |
|
|
. С другой стороны, по |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
условию примера |
|
|
|
|
|
. Тогда имеем второе равенство |
|
|
|||||
|
|
|
|
|
|
||||||||
Таким образом, |
для |
нахождения постоянных |
|
|
имеем следующую |
||||||||
систему линейных алгебраических уравнений: |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
106 |
|
|
|
|
|

Её решениями являются числа |
. |
|
|
||
Частным решением является функция |
|
|
. |
||
|
|||||
Ответ: |
|
. |
|
|
|
|
|
|
|
||
Пример 9. Указать вид, в котором надо искать частное решение линейного
неоднородного уравнения второго порядка |
|
|
|
если |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||
Решение. |
Пусть |
коэффициенты |
уравнения |
|
||||||||
постоянны |
и |
правая |
часть |
имеет |
вид |
|
где |
есть |
||||
конкретный многочлен |
степени |
|
|
с действительными коэффициентами. |
||||||||
Заметим, что |
при |
|
правая |
часть |
уравнения |
будет представлять |
собой |
|||||
многочлен |
|
. Действительное число |
будем называть контрольным числом |
|||||||||
правой части уравнения. |
|
|
|
|
|
|
|
|
|
|||
Справедливы следующие положения: |
|
|
|
|
|
|
||||||
Если |
не является корнем характеристического уравнения |
|
||||||||||
то частное решение ищется в виде |
|
|
|
|
|
|
|
|
||||
Если |
является |
двукратным корнем характеристического уравнения, то |
||||||||||
частное решение ищут в виде |
|
|
|
|
|
|
|
|
||||
Во всех трёх последних равенствах многочлен |
|
есть многочлен той же |
||||||||||
степени, то и многочлен |
, стоящий в правой части уравнения, т.е. |
|
||||||||||
Коэффициенты |
|
|
|
этого многочлена подлежат нахождению. |
||||||||
Способ их нахождения покажем в следующем примере.
Характеристическим уравнением в данном примере является уравнение
корнями которого являются числа |
|
|
Очевидно, что в ситуации 1) |
контрольное число |
и не |
совпадает ни с одним из корней характеристического уравнения. Тогда частное
решение надо искать в виде |
|
|
|
|
|
|
|
|
|
В ситуации 2) число |
, а многочленом является нулевой степени |
||||||||
. Так как совпадает с корнем |
, то частное решение надо искать в виде |
||||||||
. |
|
|
|
|
|
|
|
|
|
В последней ситуации |
|
|
|
|
(совпадает с корнем |
|
|
), а многочленом |
|
|
|
|
|
||||||
является многочлен первой |
степени |
. Тогда |
частное решение надо |
||||||
искать в виде |
|
|
|
|
|
107 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|

Ответы: 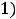
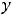

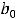
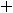
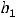
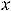
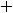
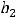
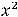

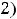
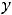

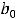
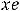
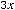

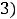
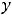

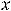
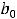
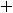
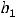
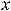
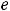

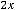

Пример 10. Найти общее решение неоднородного дифференциального уравнения 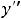

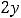

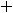
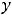

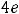
 .
.
Решение. Решение любого линейного неоднородного дифференциального
уравнения имеет следующую структуру: |
, где |
есть общее решение |
|
соответствующего приведённого однородного |
уравнения |
, а |
– некоторое |
частное решение самого неоднородного уравнения. Нахождение функций 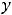 и
и 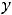 описано в предыдущих примерах 7 и 9.
описано в предыдущих примерах 7 и 9.
Характеристическим уравнением приведённого однородного уравнения
|
|
|
|
является |
алгебраическое |
уравнение |
|
|
или |
|
|
|
|
|
|
||||||
|
|
|
|
Оно имеет двукратный корень |
. Тогда |
. |
||||
|
|
|
|
|||||||
|
Теперь надо найти какое-нибудь частное решение |
самого неоднородного |
||||||||
уравнения. Его правая часть |
имеет вид, описанный в примере 9. |
|||||||||
Контрольное число |
совпадает |
с корнем |
характеристического |
|||||||
уравнения, который является двукратным. Многочленом является многочлен
нулевой степени |
. Тогда |
|
и частное решение ищется в виде |
|||
. Остаётся найти число . |
|
|
|
|||
Для нахождения |
находим первую и вторую производные функции |
|||||
, после чего |
подставляем в исходное неоднородное уравнение. |
|||||
Дифференцируя функцию, получаем |
|
|
|
|||
. Подставляя |
в уравнение, приходим к равенству |
|
||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
Сократив последнее |
равенство |
на |
и сгруппировав члены |
квадратной |
||
скобки, получаем равенство |
. Следовательно, |
. |
|
|||
Итак, частным решением исходного уравнения является функция |
. |
|||||
Общее решение уравнения определяется равенством |
|
|
||||
Ответ: 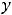

Пример 11. Найти общее решение системы дифференциальных уравнений
Решение. Систему решим методом исключения из неё одной из неизвестных функций 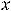
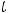
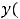
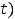 . Тогда на первом этапе система сведётся к решению линейного дифференциального уравнения второго порядка с одной неизвестной
. Тогда на первом этапе система сведётся к решению линейного дифференциального уравнения второго порядка с одной неизвестной
108
