
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание
y |
y |
0 |
x |
0 |
x |
|
|
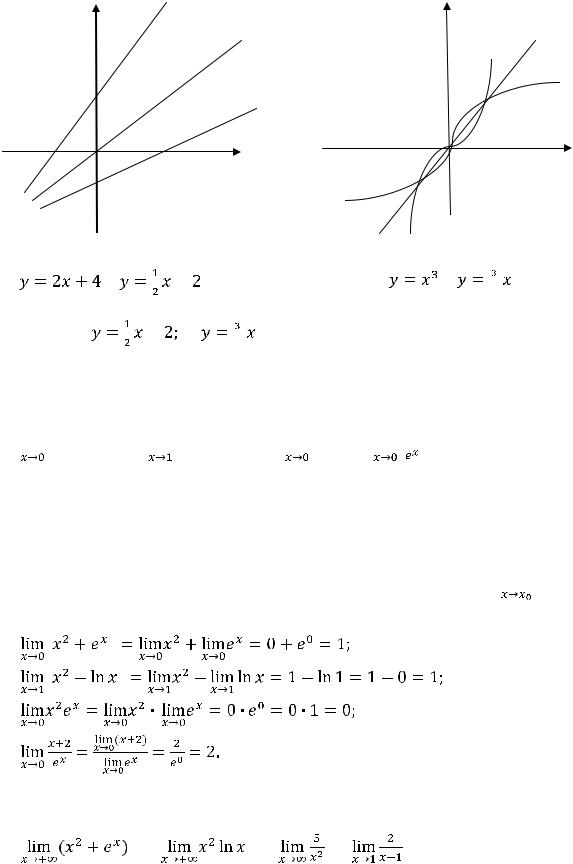
Рисунок 3 – Графики функций |
|
Рисунок 4 – Графики функций |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
и |
|
|
|
|
|
и |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: 1) |
|
|
|
|
|
|
2) |
. |
|
|
|||
|
|
|
|
|
|||||||||
Модуль 2. Пределы и непрерывность
Пример 1. Найти следующие пределы:
1) 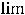
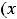
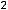
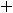
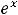
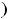 ; 2)
; 2) 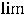
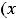
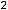

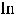
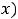 ; 3)
; 3) 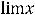
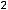
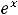 ; 4)
; 4) 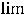
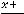
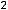 .
.
Решение. При вычислении этих пределов применимы теоремы о пределах суммы, разности, произведения и частного двух функций, если пределы соответствующих функций конечны и в случае дроби предел её знаменателя отличен от нуля. При этом воспользуемся тем, что в случае непрерывной функции её предел в точке 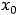 равен значению функции в этой точке
равен значению функции в этой точке 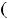
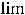
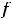
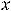


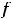
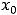
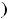 . Воспользовавшись сказанным, получим следующее:
. Воспользовавшись сказанным, получим следующее:
1) |
|
|
|
|
2) |
|
|
|
|
3) |
|
|
|
|
4) |
|
|
|
|
Ответ: 1) 1; 2) 1; 3) 0; 4) 2. |
|
|
|
|
Пример 2. Найти пределы: |
|
|
|
|
1) |
; 2) |
; 3) |
; 4) |
. |
34

Решение. В данном примере имеем особые случаи, когда упомянутые теоремы о пределах суммы, разности, произведения и частного ответа не дают. Однако ответы легко получить. Проведём очевидные записи:
1) 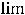
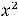
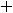
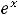
 2)
2) 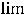
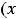
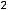
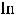
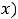
 3) )
3) ) 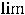
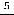

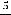

4) 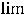
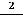

В третьем примере применена теорема о том, что величина, обратная к бесконечно большой, будет бесконечно малой величиной (условная запись
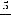

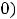 . В четвёртом примере можно применить теорему о том, что величина,
. В четвёртом примере можно применить теорему о том, что величина,
обратная к бесконечно малой, будет бесконечно большой величиной (условная запись 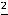

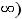

Ответ: 1) 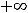 ; 2) +
; 2) +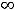 ; 3) 0; 4)
; 3) 0; 4) 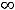 .
.
Пример 3. Вычислить следующие пределы:
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
6) |
|
; |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
8) |
|
|
|
|
|
|
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
9) |
|
|
; |
|
|
|
|
|
|
|
|
|
10) |
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
12) |
|
|
|
|
|
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
13) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
14) |
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. В этом примере рассматриваются простейшие случаи на раскрытие неопределённостей. Неопределённости возникают при вычислении пределов суммы, разности, произведения, частного двух функций и степеннопоказательного выражения, когда основные теоремы, как и в особых случаях примера 2, неприменимы. Различают неопределённости следующих видов
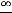

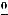

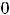

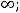
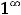

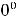

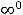
 В этих ситуациях никакого общего заключения о пределе сделать нельзя. В зависимости от участвующих в выражениях функций возможны различные ответы: пределом является конечное число (в частности,
В этих ситуациях никакого общего заключения о пределе сделать нельзя. В зависимости от участвующих в выражениях функций возможны различные ответы: пределом является конечное число (в частности,
35
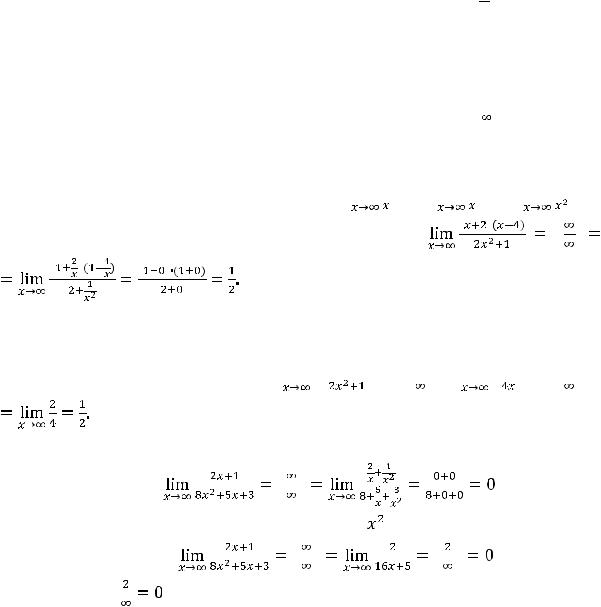
нуль), предел бесконечен, предела нет (ни конечного, ни бесконечного). Когда при исследовании предел будет установлен, то говорят, что неопределённость раскрыта.
При раскрытии неопределённостей применяются различные приёмы: преобразование выражения с последующим применением основных теорем о пределах и особых случаев, метод замены бесконечно малых величин на эквивалентные им, метод сведения к известным замечательным пределам, правило Лопиталя. Для некоторых неопределённостей применимы различные из этих приёмов, иногда они используются совместно. Действие некоторых из этих методов уже показывалось в заданиях в решениями (см. стр. 9 11). Для более глубокого понимания теории пределов читателю будет полезно обратиться к рекомендуемой литературе.
Приступим к вычислению выписанных пределов.
В первом случае, очевидно, имеем неопределённость вида 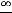 . Преобразуем выражение, разделив числитель и знаменатель этой дроби на
. Преобразуем выражение, разделив числитель и знаменатель этой дроби на 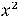 , т.е. на высшую степень
, т.е. на высшую степень 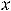 числителя и знаменателя. Далее воспользуемся теоремами о пределе частного, произведения, суммы и тем, что
числителя и знаменателя. Далее воспользуемся теоремами о пределе частного, произведения, суммы и тем, что 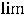
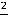

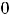 ,
, 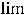
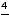

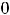 ,
, 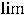
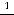

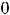
(см. рассуждения примера 2). В результате получим
Здесь и далее в скобках будем помечать вид
неопределённости.
В этом случае ещё проще получить ответ, применив последовательно два раза правило Лопиталя. Действительно, 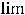
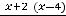

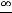

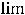
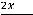

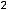

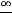

Второй случай разберём сначала с помощью метода преобразования
выражения. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(при этом |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
числитель |
и знаменатель дроби разделили на |
|
). Действуя же по правилу |
|||||||||||||||||||
Лопиталя, |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(применена |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
условная запись |
|
|
, см. пример 2). |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
36

Вычислим третий предел, в котором имеем дело с неопределённостью 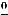 . Так как при
. Так как при 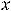
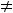
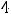 справедливо равенство
справедливо равенство 

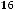

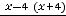

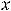
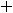
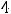 , то
, то 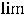


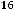


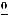

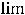
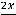

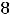
 Применив правило Лопиталя, получим тот же ответ:
Применив правило Лопиталя, получим тот же ответ:
Для вычисления предела 4), представляющего неопределённость вида 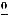 ,
,
разложим числитель и знаменатель на множители, предварительно найдя корни
многочленов. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
преобразованную дробь |
сократили |
|
на множитель |
|
|
; |
такое сокращение |
|||||||||||||||||
|
|
|||||||||||||||||||||||
возможно, так как |
|
|
при |
стремится к нулю, но не |
равно нулю. |
|||||||||||||||||||
|
||||||||||||||||||||||||
Теперь для вычисления этого предела применим правило Лопиталя. В
результате получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. тот же ответ. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае 5) также имеем неопределённость вида |
|
|
|
Применим подстановку |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
, при этом справедливо соответствие |
|
|
|
|
|
|
|
. При этом |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В следующей ситуации 6) имеем уже неопределённость вида
Преобразовав исходное выражение |
|
|
к виду |
|
|
|
, получим неопределённость |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, к которой применим правило Лопиталя. В итоге получим |
||||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, при вычислении |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
этого предела применили два приёма |
|
|
преобразование выражения и правило |
||||||||||||||||||
|
|
||||||||||||||||||||
Лопиталя. |
|
|
|
|
|
|
|
||||||||||||||
|
В случае 5) также имеем неопределённость вида |
|
|
. Применим подстановку |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, при этом справедливо соответствие |
|
|
|
при этом |
= , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
37

|
В следующей ситуации 6) |
имеем уже |
неопределённость вида 0 |
. |
|||||||||||||||||
Преобразовав исходное выражение |
|
|
к виду |
|
|
|
, получим неопределённость |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, к которой применим правило |
Лопиталя. В |
итоге получим |
|
|||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при вычислении этого предела применили два приёма – преобразование выражения и правило Лопиталя.
В заданиях 7) и 8) имеем неопределённости вида 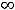

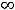 . В обоих случаях исходную функцию преобразуют, умножая и деля её на так называемое
. В обоих случаях исходную функцию преобразуют, умножая и деля её на так называемое
сопряжённое к ней выражение (в 7) на |
|
|
|
в 8) на |
|
). Тогда для |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
предела |
7) |
|
|
|
|
|
|
|
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае же 8) имеем

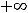 . Во второй ситуации,
. Во второй ситуации,
кроме преобразования выражения, которое привело к другой неопределённости, применили ещё правило Лопиталя.
Приступим к вычислению предела 9). Здесь можно применить три метода раскрытия этой неопределённости, которая, очевидно, имеет вид 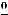 .
.
Исходное выражение преобразуем, чтобы результат свести к применению первого замечательного предела 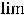




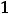 . Итак,
. Итак, 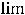

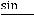
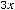

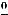

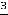 .
.
Теперь применим метод замены бесконечно малых величин на эквивалентные
им (см. стр. 10 |
|
11). Так как при |
, |
имеем эквивалентность |
||||||||||||
|
||||||||||||||||
(следовательно, |
и |
), то |
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|||||||||||
Теперь будем |
действовать по |
правилу |
Лопиталя: |
|
|
|
|
|||||||||
|
|
|||||||||||||||


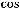
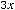


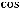


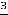 .
.
Предел 10) можно вычислить с помощью сведения к первому замечательному пределу и по правилу Лопиталя, что предоставляем читателю. Проще всего
38

заменить функции на эквивалентные им (при 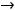 имеем эквивалентности:
имеем эквивалентности:
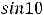
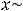
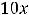
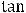
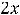
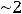
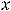 ). Тогда
). Тогда 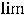
В заданиях 11) и 12) имеют место неопределенности вида 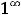 , так как пределы оснований этих степенно-показательных выражений равны единице, а пределы показателей бесконечны (+
, так как пределы оснований этих степенно-показательных выражений равны единице, а пределы показателей бесконечны (+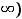 . Оба предела будем сводить ко второму
. Оба предела будем сводить ко второму
замечательному пределу |
|
. Для этого будем |
|
проводить соответствующие преобразования исходных функций.
В случае 11) имеем следующее:

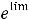
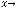
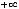
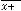


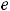
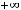

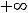 . При вычислении воспользовались тем, что предел квадратной скобки (основания нового степенно-показательного выражения) равен
. При вычислении воспользовались тем, что предел квадратной скобки (основания нового степенно-показательного выражения) равен 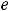 , а предел показателя, очевидно, есть (
, а предел показателя, очевидно, есть (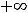
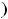 . Получили особый случай
. Получили особый случай 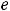
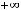 , но так как
, но так как 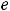
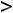
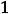 , то
, то 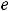
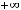 =
=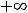 .
.
В случае 12) имеем

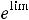
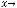

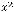

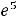 . При этом воспользовались тем, что предел квадратной скобки равен числу
. При этом воспользовались тем, что предел квадратной скобки равен числу 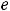 ( это легко понять с помощью замены переменной
( это легко понять с помощью замены переменной 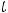

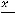 ),
),
апредел показателя равен 5.
Вслучае предела 13) имеем неопределённость 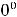 . Для вычисления предела
. Для вычисления предела
прологарифмируем равенство |
по основанию |
. |
Получим, |
что |
|||
. Теперь перейдём |
в |
равенстве |
|
|
к |
пределу при |
|
: |
|
(воспользовались |
уже |
вычисленным |
|||
пределом 6)). Итак, |
. |
Так как |
логарифмическая |
функция |
|||
непрерывна в своей области определения, то знак предела и знак функции
можно переставить местами. Тогда |
и из равенства |
||
|
на основании определения логарифма имеем |
|
|
т.е. |
. |
|
|
В последней ситуации 14), очевидно, |
имеем неопределенность |
. Будем |
|
проводить действия, аналогичные предыдущему случаю. Прологарифмируем
равенство |
|
по основанию |
, в новом равенстве перейдём к пределу и |
|
|||
|
|
|
39 |
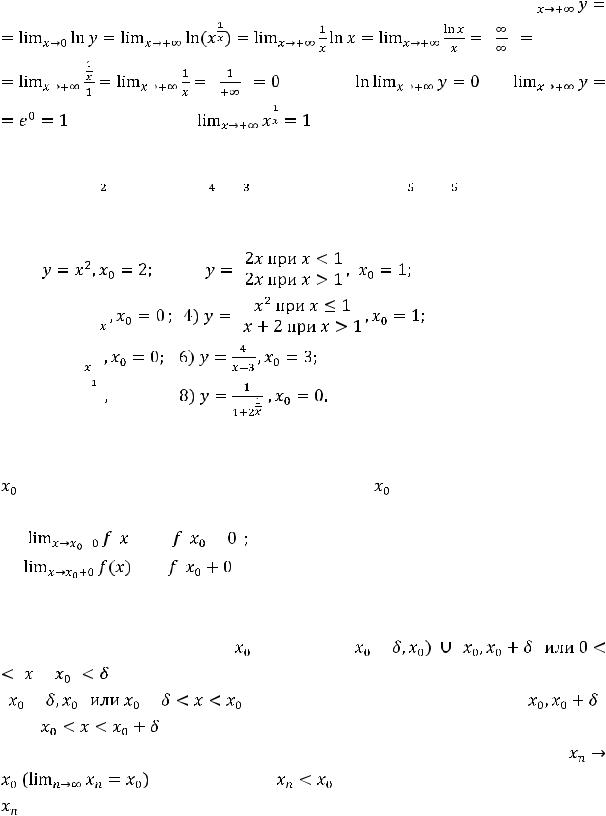
переставим символы предела и функции. В результате получим 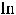
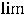
. Так как |
, то |
. Таким образом, |
|
. |
|
Ответ: 1) 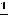 ; 2) 0; 3) 8; 4)
; 2) 0; 3) 8; 4) 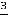 ; 5)
; 5) 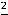 ; 6) 0; 7) 0; 8) +
; 6) 0; 7) 0; 8) +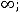
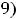
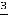 ; 10)
; 10) 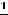 ; 11) +
; 11) +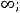 12)
12) 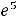 ; 13) 1; 14) 1.
; 13) 1; 14) 1.
Пример 4. Найти в указанных точках 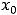 односторонние пределы функций:
односторонние пределы функций:
1) |
2) |
3) 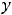

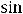
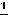
5) 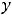



7) 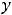

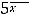


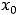

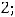
Решение. Кроме понятия предела функции 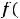
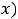 в конечной точке
в конечной точке 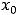 , существуют ещё понятия односторонних пределов в этой точке: предела слева в
, существуют ещё понятия односторонних пределов в этой точке: предела слева в
(левостороннего предела) |
и предела справа в |
(правостороннего предела). |
|||
Эти пределы соответственно обозначаются так: |
|
||||
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
или |
. |
|
|
Односторонние пределы на языке окрестностей определяются почти так же, как обычный предел в точке, но в определении рассматривается не вся
проколотая окрестность точки |
(множество ( |
|
|
|
||||||||
|
|
|||||||||||
|
|
|
|
), |
|
а |
только |
соответствующая |
полуокрестность |
|||
|
|
|||||||||||
|
|
|
|
|
|
|
|
в случае левостороннего предела и |
||||
|
|
|
|
|
|
|
|
|||||
или |
|
|
в случае правостороннего предела. При определении |
|||||||||
предела на языке |
последовательностей должно выполняться условие |
|||||||||||
|
|
|
|
|
|
и неравенство |
в случае левостороннего предела, |
|||||
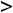
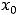 в случае правостороннего предела.
в случае правостороннего предела.
Любой из односторонних пределов может оказаться бесконечностью.
Если функция в какой-нибудь внутренней точке промежутка имеет конечный предел, то она имеет в этой точке и оба односторонние пределы, причём все три
40

предела равны, т.е. 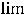
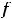
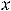

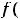
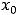

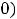

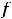
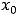
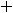
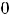 но функция может иметь односторонние пределы и при отсутствии обычного предела в точке.
но функция может иметь односторонние пределы и при отсутствии обычного предела в точке.
Если же функция в некоторой точке имеет односторонние пределы, равные между собой, то это общее значение будет и пределом функции в этой точке.
Ещё раз подчеркнём, что о любом пределе функции в точке 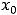 можно говорить как в случае, когда функция в этой точке определена, так и в случае, когда она в ней не определена. Но эта точка должна быть всегда предельной точкой (точкой сгущения) области определения функции.
можно говорить как в случае, когда функция в этой точке определена, так и в случае, когда она в ней не определена. Но эта точка должна быть всегда предельной точкой (точкой сгущения) области определения функции.
В первом задании в точке 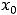

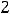 определена и имеет все три предела (обычный и оба односторонние), значениями которых является общее число 4.
определена и имеет все три предела (обычный и оба односторонние), значениями которых является общее число 4.
Во втором случае функция по самому способу её задания не определена в
точке |
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
|
|
|
|
определена для всех |
Её график заключён между |
||||||
|
|
|
|
|||||||||
горизонтальными прямыми |
|
и |
причём волнами сжимается к оси |
|||||||||
|
||||||||||||
ординат. Все три предела не существуют. |
|
|
|
|||||||||
В случае функции 4), которая в точке |
определена и имеет значение |
|||||||||||
|
, обычного предела в этой точке нет. Оба односторонние пределы |
|||||||||||
существуют, при этом |
|
|
|
|
, т.е. односторонние |
|||||||
пределы различны. |
|
|
|
|
|
|||||||
Функция |
|
|
|
в точке |
|
не определена. Известно, что |
|
. |
||||
|
|
|
|
|
||||||||
Этот предел называется первым замечательным пределом. Оба односторонние
пределы также равны единице. |
|
|
|
|
|
|
|
|||||||||||
В задании 6) имеем следующее: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом легко убедиться, подставляя в функцию значения, |
близкие к |
и |
||||||||||||||||
находящиеся слева (например, |
|
|
|
|
, справа (например, |
|
||||||||||||
|
|
|
|
. Все пределы являются бесконечностями, при этом |
||||||||||||||
односторонние пределы есть бесконечности со знаком. |
|
|
||||||||||||||||
В заданиях 7) и 8) функции в |
указанных точках |
не определены. Их |
||||||||||||||||
пределы (обычные) в этих точках не существуют. При этом односторонние пределы таковы: 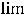
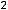

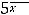



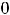
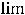
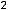

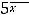



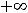
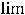


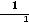

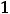
41


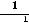

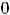 . При
. При 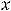
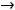
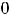

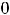 применяют ещё запись
применяют ещё запись 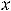
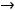
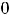
 , а при
, а при 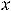
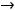
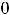
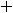
- |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Читателю рекомендуем указать виды графиков всех функций этого примера. |
|||||||||||||||||||
Ответ: |
1) |
|
|
|
|
2) |
|
|
3) |
||||||||||
|
|
|
|
|
|||||||||||||||
односторонние пределы |
не существуют; |
4) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5. Исследовать на непрерывность следующие функции: 1)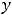

Решение. Обе функции определены на |
промежутке (- |
. |
Функция |
||||||
называется непрерывной в любой точке |
|
её области определения, если |
|||||||
выполняется равенство |
, где |
|
|
есть приращение аргумента, а |
|||||
|
|
есть приращение функции в точке |
. Определение |
||||||
|
|
||||||||
означает, что бесконечно малому приращению аргумента в точке |
|
должно |
|||||||
соответствовать |
|
бесконечно |
малое |
приращение |
функции |
(из |
|||
|
|
|
. |
|
|
Обозначения |
|
|
|
рассматриваются как единые символы. |
|
|
|
|
|
|
|||
Для функции |
|
имеем |
|
|
|
|
|
. Тогда в |
|
|
|
|
|
|
|
||||
любой точке из области определения |
|
|
|
|
|
|
|||

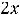
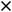
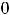
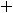
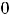

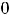 , что и означает непрерывность функции на её области определения (-
, что и означает непрерывность функции на её области определения (-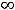
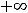
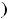 .
.
При исследовании второй функции воспользуемся тригонометрическим тождеством
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Покажем, |
что |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
величина |
|
при |
|
|
|
|
является бесконечно малой. Действительно, на |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
основании |
|
первого |
|
|
|
|
|
|
замечательного |
|
|
предела |
имеем |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так |
как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
величина |
|
|
|
|
|
|
|
|
является ограниченной |
|
|
|
|
|
|
|
то |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
представляет собой произведение ограниченной величины на бесконечно малую
42

величину и, следовательно, является бесконечно малой величиной. Таким образом, 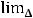

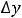

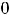 , что и означает непрерывность этой функции.
, что и означает непрерывность этой функции.
Ответ: обе функции непрерывны на (-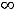
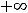
 Пример 6. Для следующих функций указать точки разрыва и их характер:
Пример 6. Для следующих функций указать точки разрыва и их характер:
1)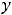

2) |
|
|
|
|
3) |
|
|
|
|
|
|
|
|
||
4) |
|
|
|
|
5) |
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|||||||
6) |
|
|
|
|
7) |
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
||||||||
8) |
|
|
|
9) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
10) |
|
|
|
|
|
|
11) |
|
|
|
|
|
12) |
|
|
|
|
. |
13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
14) |
|
|
|
|
|
|
15) |
|
. |
|||
Решение. Функция |
называется непрерывной в точке , если она |
|
определена в этой точке (существует значение |
, имеет конечный предел |
|
и выполняется равенство |
(предел функции в |
|
точке совпадает со значением функции в ней).
Требования наличия предела означает, что функция должна быть определена и в некоторой окрестности точки 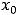 .
.
Из данного определения следует, что о непрерывности функции можно говорить лишь по отношению к точкам, в которых функция определена. Отметим, что при определении предела в точке такое условие не ставится;
предел может |
существовать и в точках, в которых функция не определена |
(значение |
в определении предела не участвует). |
Кроме того, используется и понятие так называемой односторонней непрерывности.
43

Функция |
называется непрерывной в точке |
слева (справа), если |
|||
|
|
|
( |
). Это |
означает, что и при |
односторонней непрерывности функция должна быть определена в этой точке. Легко понять, что функция, непрерывная во внутренней точке своей области
определения, будет одновременно непрерывна в этой точке слева и справа. Справедливо и обратное утверждение: если функция непрерывна слева и справа в некоторой внутренней точке, то она будет и непрерывной в этой точке. Однако функция может быть непрерывна только с одной стороны.
Функция 

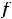
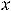 называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Если таким промежутком является отрезок [
называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Если таким промежутком является отрезок [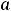
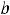 ] (или любой из полуотрезков [
] (или любой из полуотрезков [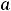
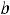 ), (
), (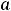
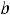 ]), то на принадлежащих ему концах подразумевается односторонняя непрерывность: в
]), то на принадлежащих ему концах подразумевается односторонняя непрерывность: в
точке |
непрерывность справа ( |
, а в точке |
|
непрерывность |
||
|
||||||
слева ( |
|
|
. |
|
|
|
|
|
|
|
|||
Точкой разрыва функции называется всякая точка, в которой функция определена, но не непрерывна. Тогда либо функция в этой точке не имеет конечного предела, либо конечный предел в этой точке существует, но не
совпадает со значением функции в ней ( |
. |
Термин «непрерывная функция» связан с |
представлением непрерывности |
(сплошности) кривой. Являющейся графиком функции на плоскости. Такая кривая может быть получена непрерывным движением точки по ней. В связи с этим к точкам разрыва функции обычно причисляют ещё точки, в которых функция не определена, но которые являются предельными точками (точками сгущения) её области определения. Напомним, что точка 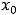 называется предельной точкой некоторого множества, если в любой её окрестности имеется хотя бы одна точка этого множества, отличная от точки
называется предельной точкой некоторого множества, если в любой её окрестности имеется хотя бы одна точка этого множества, отличная от точки 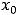 .
.
Для разрывов функции проводится некоторая классификация.
Если в точке 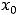 функция имеет разрыв и хотя бы один из односторонних пределов в ней бесконечен или вообще не существует, это разрыв называется разрывом второго рода.
функция имеет разрыв и хотя бы один из односторонних пределов в ней бесконечен или вообще не существует, это разрыв называется разрывом второго рода.
Все остальные разрывы относят к разрывам первого рода. К таким разрывам относят и так называемые устранимые разрывы, которые поясним ниже при
разборе заданий. |
|
Первая функция, называемая функцией Дирихес, определена на |
, |
т. е. на всей числовой оси. Ни в одной точке она не имеет предела (ни конечного,
44
ни бесконечного). Следовательно, она терпит разрыв второго рода в каждой точке области определения. Её график изобразить невозможно, но можно представить мысленно. Бесконечное множество точек графика лежит на прямой 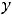

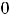 и бесконечное – на прямой
и бесконечное – на прямой 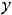

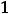 , при этом множеством значений функции является конечное множество {0, 1}.
, при этом множеством значений функции является конечное множество {0, 1}.
Функция задания 2) также определена на всей числовой оси. В частности, она определена и в точке 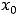

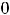 (по условию
(по условию 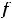
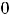

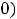 . Однако
. Однако 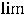

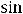
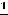 не существует (в нуле нет ни конечного, ни бесконечного предела, см. задание 3) из примера 4). Следовательно, в точке
не существует (в нуле нет ни конечного, ни бесконечного предела, см. задание 3) из примера 4). Следовательно, в точке 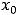

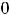 имеется разрыв второго рода. График этой функции изобразить очень трудно. В окрестности нуля он совершает бесконечное множество колебаний, сжимаясь к оси ординат.
имеется разрыв второго рода. График этой функции изобразить очень трудно. В окрестности нуля он совершает бесконечное множество колебаний, сжимаясь к оси ординат.
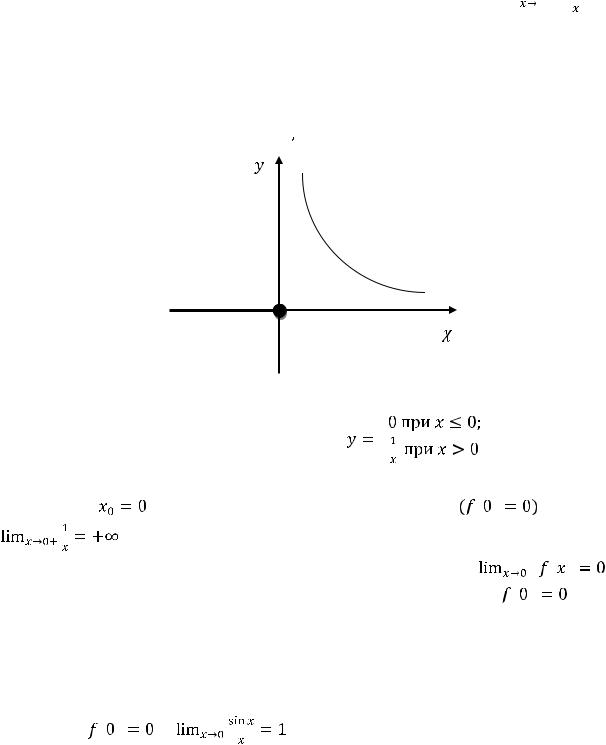
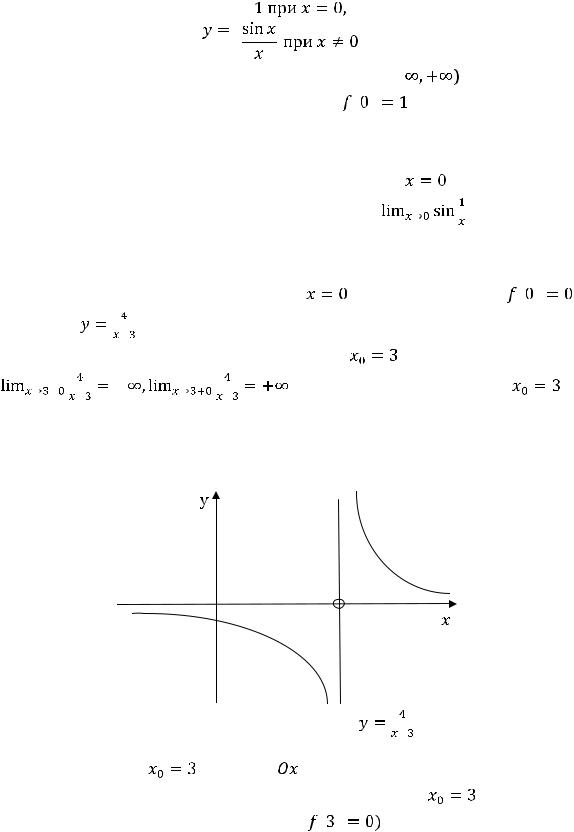
Третья функция определена на 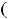

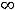
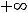
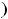 , её график изображён на рисунке 5.
, её график изображён на рисунке 5.
|
|
|
Рисунок 5 – |
График функции |
|
|
|
|
|
В точке |
она по |
самому заданию |
определена |
|
, однако |
||||
|
|
|
. Так как правосторонний предел в нуле равен бесконечности, то |
||||||
|
|
|
|||||||
в этой точке происходит разрыв второго рода. В то же время |
|
|
|||||||
(левосторонний |
предел в нуле равен нулю, |
см. рисунок 5) и |
|
, т.е. |
|||||
левосторонний предел в нуле совпадает со значением функции в нуле. Таким образом, при 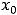

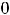 имеется непрерывность слева, а справа – разрыв. При построении графика совершается бесконечный скачок.
имеется непрерывность слева, а справа – разрыв. При построении графика совершается бесконечный скачок.
В задании 4) функция определена а всей координатной прямой. При этом по
её заданию |
, а |
|
(первый замечательный предел) получили |
|
|||
|
|
45 |
|
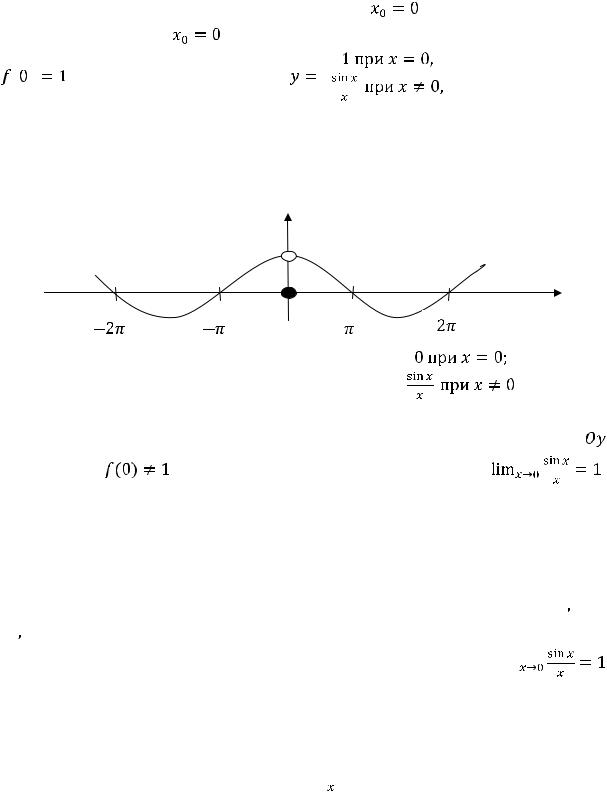
ситуацию, что предел в точке 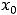

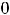 не совпадает со значнием функции в этой точке. Так как предел существует и конечен, то имеем разрыв первого рода. Этот разрыв относят к устранимым разрывам. Его можно устранить, переопределив
не совпадает со значнием функции в этой точке. Так как предел существует и конечен, то имеем разрыв первого рода. Этот разрыв относят к устранимым разрывам. Его можно устранить, переопределив
(изменив) значение функции только в точке |
. Для этого в качестве |
||||
значения |
функции в |
надо взять предельное |
значение, т.е. положить |
||
. |
Получим новую функцию |
|
|
которая от прежней |
|
отличается только значением в одной точке 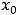

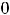 , но которая в этой точке является непрерывной. Любое другое переопределение (изменение) значения функции в нуле, кроме
, но которая в этой точке является непрерывной. Любое другое переопределение (изменение) значения функции в нуле, кроме 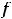
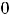

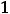 , разрыва в этой точке не устранит. На рисунке 6 указан примерный вид графика исходной функции.
, разрыва в этой точке не устранит. На рисунке 6 указан примерный вид графика исходной функции.
0
Рисунок 6 – График функции 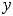

Жирная точка на оси 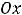 означает, что
означает, что 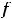
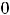

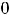 ; выколотая точка на оси
; выколотая точка на оси
означает, что |
. Рисунком 6 пояснено и утверждение, что |
|
. |
|
В нуле нет ни левосторонней, ни правосторонней непрерывности.
Читатель без труда может изобразить график переопределённой функции, уже непрерывной в нуле и на всей области определения.
В ситуации 5) функция определена для всех 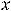 , кроме
, кроме 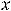

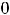 . Очевидно, что эта точка является предельной точкой для множества (-
. Очевидно, что эта точка является предельной точкой для множества (-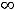
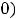
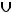
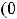
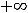
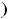 ,являющегося областью определения рассматриваемой функции.
,являющегося областью определения рассматриваемой функции.
Следовательно, её надо считать точкой разрыва функции. Так как 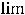
(предел существует и конечен), то имеем разрыв первого рода. Разрыв относят к устранимым разрывам. Действительно, разрыв устраняется следующим образом. Надо доопределить функцию в нуле, а именно: положить 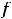
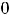

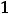 (за значение
(за значение 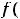
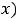 в нуле приняли предельное значение
в нуле приняли предельное значение 
 в этой точке). Новая функция (уже применявшаяся в задании 4))
в этой точке). Новая функция (уже применявшаяся в задании 4))
46
будет непрерывной и в нуле и на всём множестве (- |
. Любое другое |
доопределение исходной функции в нуле, кроме |
, разрыва не устранит. |
Рекомендуем читателю построить график функции 5) и сравнить с графиком
предыдущей функции 4). |
|
|
|
В следующем случае функция не определена в точке |
, которая является |
||
предельной для её области определения. При этом |
|
|
не существует |
|
|
||
(см. задание 6) примера 4). В этой точке имеет место разрыв второго рода. Рассматриваемая функция напоминает функцию 2) этого примера. Различие
состоит лишь в том, что функция 2) в точке |
|
принимает значение |
. |
||||||||||||||||
Функция |
|
|
|
|
|
рассматривалась в |
задании 6) примера 4. При |
этом |
|||||||||||
|
|
|
|
|
|||||||||||||||
установлено, что односторонние пределы в точке |
таковы: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
Это означает, что в точке |
(в |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
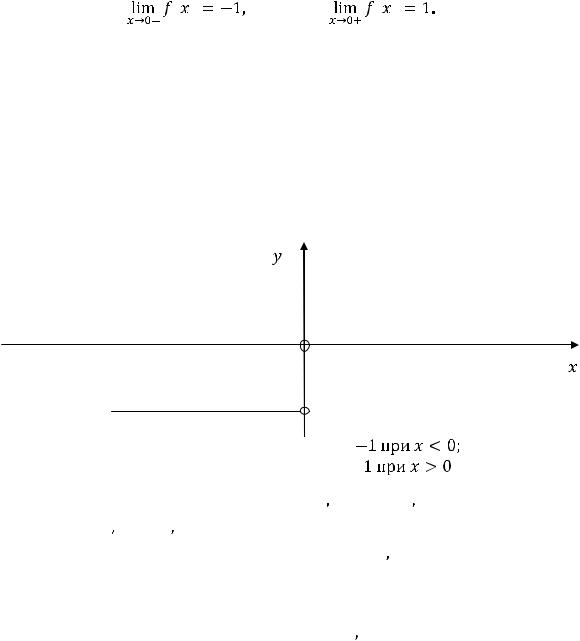
ней функция не определена) происходит разрыв второго рода. Такой разрыв в точке принято называть ещё разрывом с бесконечным скачком. Функция на области определения не ограничена. На рисунке 7 изображён её график.
3
|
Рисунок 7 – График функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Выколотая точка |
на оси |
означает, |
|
что |
функция в ней не |
||||
определена. Разрыв сохраняется, если функцию в точке |
|
доопределим |
|||||||
каким-нибудь образом (например, положим |
|
. |
|
|
|
|
|
|
|
Сделаем важное замечание относительно функций 5) |
|
7). Каждая из них |
|||||||
|
|||||||||
является непрерывной на своей области определения (см. приведённое выше определение непрерывности функции на промежутке). Это не противоречит
47
тому, что они имеют по одной точке разрыва, так как указанные точки разрыва соответствующей области определения функции не принадлежат. Каждая из этих функций будет непрерывной на любом промежутке, являющемся частью своей области определения (сужение функции непрерывно).
Обычно функцию 8) обозначают 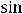
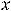 (знак
(знак 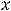 ). Она не определена в нуле. Односторонние пределы в этой точке существуют и конечны:
). Она не определена в нуле. Односторонние пределы в этой точке существуют и конечны:
Таким образом, в нуле имеем разрыв первого рода. Этот разрыв называют ещё разрывом с конечным скачком. При таком разрыве в точке 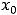 величину
величину 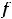
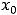
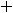
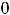

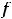
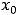

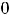 , т.е. разность между правосторонним и левосторонним пределами в точке
, т.е. разность между правосторонним и левосторонним пределами в точке 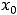 , называют скачком функции. Для этой функции скачок в нуле есть величина
, называют скачком функции. Для этой функции скачок в нуле есть величина 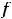
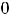
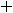

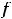
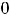


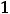


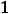

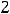
 При скачке разрыв не устраним при любом доопределении функции в точке разрыва
При скачке разрыв не устраним при любом доопределении функции в точке разрыва 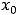 . Эта функция в нуле не обладает односторонней неопределённостью. Её график изображён ниже на рисунке 8.
. Эта функция в нуле не обладает односторонней неопределённостью. Её график изображён ниже на рисунке 8.
1 
0
-1
Рисунок 8 – График функции 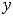

Выколотые точки означают, что 
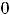
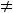
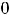
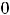
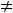

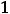
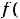
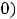
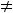
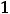
 На области определения
На области определения 
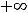
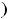 функция является непрерывной.
функция является непрерывной.
Функция 9) определена на всей числовой оси 
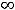
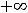
 можно считать, что предыдущая функция доопределена в точке
можно считать, что предыдущая функция доопределена в точке 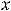

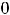 нулём
нулём 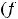
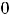

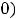 . И всё же в нуле имеем разрыв первого рода. Так как точка
. И всё же в нуле имеем разрыв первого рода. Так как точка 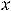

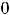 уже входит в область определения функции, то на этой области
уже входит в область определения функции, то на этой области 
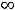
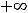 функцию надо считать разрывной из-за разрыва в точке
функцию надо считать разрывной из-за разрыва в точке 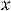

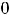 . График функции изображён на рисунке
. График функции изображён на рисунке
9.
48
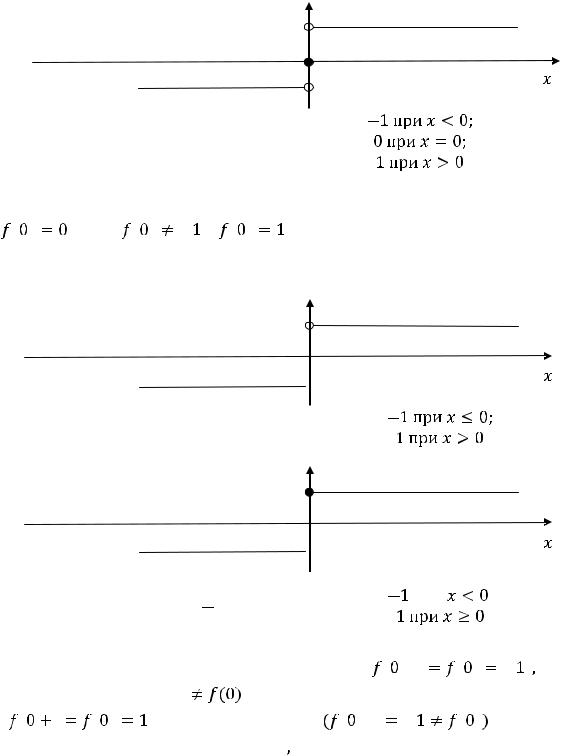
y 1
-1
Рисунок 9 – График функции 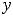

Согласно принятым |
ранее |
обозначениям на этом чертеже показано, что |
|
(тогда |
|
и |
). |
|
|||
Обратимся к функциям 10) и 11), которые определены на всей числовой оси. Ниже построены их графики (рисунки 10 и 11).
1
0  -1
-1
Рисунок 10 – График функции 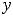

1
0  -1
-1
Рисунок 11 График функции 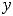

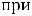
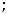 Обе функции определены в нуле и имеют в этой точке разрыв первого рода.
Обе функции определены в нуле и имеют в этой точке разрыв первого рода.
При этом функция 10) непрерывна в нуле слева |
|
|
|
|
|
не имеет |
||
|
|
|
|
|
||||
разрыв справа (f(0+)=1 |
). Функция 11) |
непрерывна в |
нуле справа |
|||||
, но разрывна слева |
|
|
|
. |
Обе функции |
|||
|
|
|||||||
разрывны на области определения (-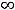
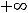
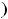
 Для исследования функции 12) и 13) построим их графики (рисунки 12, 13).
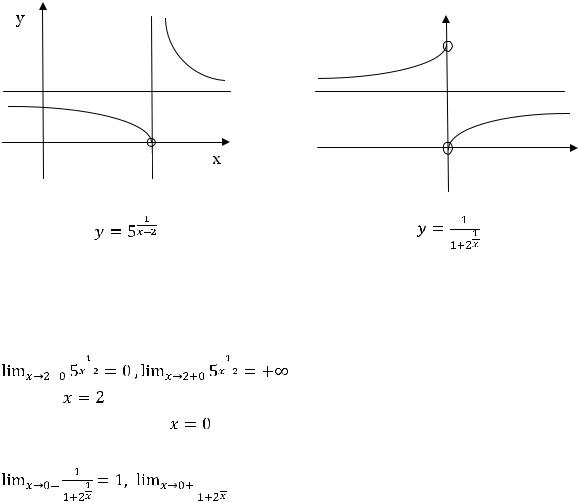
Для исследования функции 12) и 13) построим их графики (рисунки 12, 13).
49
|
|
|
y |
|
|
|
|
1 |
|
|
|
|
|
y=0,5 |
|
|
y=1 |
|
|
0 |
x=2 |
2 |
0 |
x |
Рисунок 12 – График функции |
Рисунок 13 – График функции |
|||
Рисунки позволяют сделать следующие заключения.
Функция 12) не определена в точке 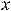

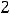 и имеет в ней разрыв второго рода, причём с бесконечным скачком. Односторонние пределы в этой точке таковы:
и имеет в ней разрыв второго рода, причём с бесконечным скачком. Односторонние пределы в этой точке таковы:
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В точке |
|
|
нет непрерывности как слева, так и справа. |
|||||||
Функция 13) в точке |
не определена, а односторонние пределы в ней |
|||||||||
таковы:
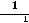

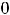 . Следовательно, в этой точке наблюдаем
. Следовательно, в этой точке наблюдаем
разрыв первого рода, причём с конечным скачком. Доопределением функции в точке 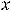

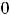 разрыв устранить невозможно. Разрыв в точке
разрыв устранить невозможно. Разрыв в точке 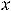

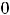 как слева, так и справа.
как слева, так и справа.
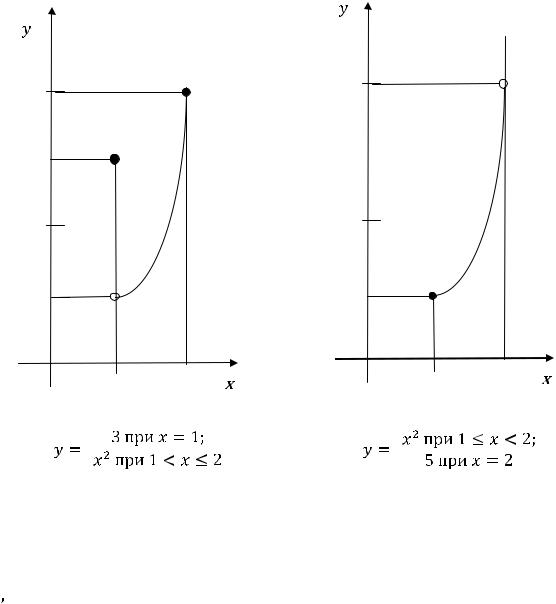
Обе функции 12) и 13) на их областях определения являются непрерывными. Две последующие функции определены на одном и том же отрезке [1,2]. При
этом первая терпит разрыв на левом конце 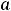

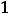 , а вторая – на правом конце
, а вторая – на правом конце 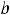

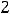 (см. рисунки 14, 15).
(см. рисунки 14, 15).
50
5 
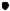
4 |
4 |
|
3
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Рисунок 15 – График функции |
|||||
Рисунок 14 – График функции |
||||||||||
Читателю предлагаем переопределить каждую функцию на соответствующем конце отрезка [1,2] так, чтобы новая функция (с изменённым значением на одном конце) стала непрерывной на всём отрезке, и указать эту функцию.
Рекомендуем также привести пример функции, определённой на отрезке [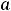
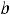 ] и имеющей разрыв второго рода на каком-нибудь из концов этого отрезка или на обоих его концах.
] и имеющей разрыв второго рода на каком-нибудь из концов этого отрезка или на обоих его концах.
Ответ: 1) в каждой точке области определения имеем разрыв второго рода; 2) в нуле имеем разрыв второго рода; 2) в нуле имеем разрыв второго рода; 3) в нуле функция имеет разрыв второго рода, причём слева непрерывна, а справаразрыв; 4) в нуле имеем разрыв первого рода, причём разрыв устранимый; 5) в нуле функция терпит разрыв первого рода, причём устранимый; 6) в нуле разрыв второго рода; 7) в точке 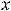

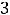 функция терпит разрыв второго рода, при этом разрыв с бесконечным скачком; 8) в точке
функция терпит разрыв второго рода, при этом разрыв с бесконечным скачком; 8) в точке 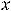

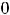 разрыв первого, причём с конечным скачком (разрыв устранить нельзя); 9) в нуле разрыв первого рода; 10) разрыв первого рода в нуле, при этом функция в нуле непрерывна слева; 11) разрыв в нуле первого рода с непрерывностью в этой точке справа; 12) в точке
разрыв первого, причём с конечным скачком (разрыв устранить нельзя); 9) в нуле разрыв первого рода; 10) разрыв первого рода в нуле, при этом функция в нуле непрерывна слева; 11) разрыв в нуле первого рода с непрерывностью в этой точке справа; 12) в точке
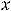

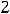 разрыв второго рода, причём с бесконечным скачком; 13) разрыв первого
разрыв второго рода, причём с бесконечным скачком; 13) разрыв первого
51
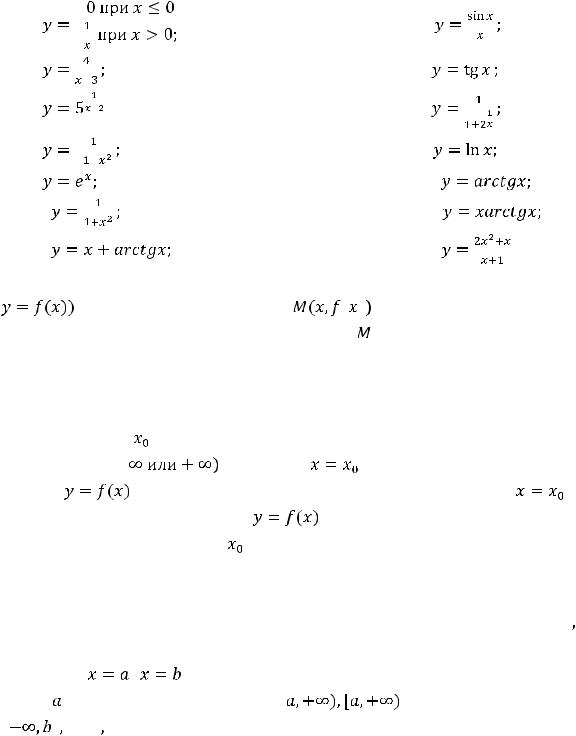
рода в нуле, при этом с конечным скачком; 14) разрыв первого рода на левом конце 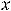

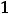 отрезка [1,2]; 15) разрыв первого рода на первом конце
отрезка [1,2]; 15) разрыв первого рода на первом конце 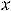

 отрезка [1,2].
отрезка [1,2].
Пример 7. Найти асимптоты следующих кривых:
1) |
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) |
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) |
|
|
|
|
|
|
; |
6) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7) |
|
|
|
|
|
|
|
|
8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9) |
|
|
|
|
|
|
|
|
10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11) |
|
|
|
|
|
|
|
|
|
12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13) |
|
|
|
|
|
|
|
|
14) |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Прямая линия называется асимптотой кривой (графика функции
, если расстояние от точки |
, лежащей на кривой, до этой |
||||
прямой стремится к нулю при удалении точки |
по какой-нибудь части кривой |
||||
в бесконечность. |
|
|
|
|
|
Различают три вида асимптот |
|
вертикальные, горизонтальные и наклонные. |
|||
|
|||||
Опишем, как их находить. |
|
|
|
|
|
Если в точке |
хотя бы один из односторонних пределов функции равен |
||||
бесконечности (- |
, то прямая |
будет вертикальной асимптотой |
|||
кривой |
. Верно и обратное утверждение: если прямая |
есть |
|||
вертикальная асимптота кривой |
|
, то хотя бы один из односторонних |
|||
пределов функции в точке |
бесконечен. |
Следовательно, для |
нахождения |
||
вертикальных асимптот функции нужно находить её точки разрыва второго рода с бесконечным скачком.
Если функция определена на каком-нибудь из промежутком 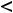
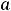
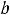
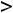 (интервале, отрезке или любом из полуотрезков), то возможны вертикальные
(интервале, отрезке или любом из полуотрезков), то возможны вертикальные
асимптоты |
, |
на границах промежутка. То же самое можно сказать о |
|
конце бесконечных промежутков ( |
и о конце в промежутков |
||
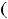

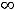
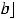 .
.
Вертикальных асимптот может быть сколько угодно, даже бесконечное число.
52

Горизонтальных асимптот не может быть более двух. Для их нахождения
надо найти пределы |
|
|
|
|
Если они конечны (соответственно |
) и различны ( |
, то есть две |
||
горизонтальные асимптоты: |
. Если |
или только один из |
||
этих двух пределов конечен, то будет одна горизонтальная асимптота. Если же таких конечных пределов нет, то нет и горизонтальных асимптот.
Наклонные асимптоты имеют вид |
|
. Такая прямая будет наклонной |
|||||||||||||
асимптотой графика функции |
|
тогда и только тогда, когда при |
|
|
|
|
|||||||||
|
|
|
|
||||||||||||
или |
|
|
будут существовать |
|
конечные пределы |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Наклонных асимптот не может быть более двух (одной при |
|
|
|
|
и одной |
||||||||||
|
|
|
|
||||||||||||
при |
). Если хотя бы один из указанных пределов (как при |
|
|
|
|
, так и |
|||||||||
|
|
|
|
||||||||||||
при |
) не существует, то соответствующей асимптоты (левосторонней |
||||||||||||||
или правосторонней) нет. |
|
|
|
|
|
|
|
|
|
|
|
||||
Отметим, что горизонтальную асимптоту |
можно считать |
частным |
|||||||||||||
случаем наклонной асимптоты |
|
. Тогда при вычислении указанного |
|||||||||||||
предела для вычисления углового |
коэффициента |
наклонной |
|
|
асимптоты |
||||||||||
получим, что он равен нулю |
. При этом должен существовать второй |
||||||||||||||
конечный |
предел |
|
|
|
т.е. |
тот |
предел, |
||||||||
|
|
|
|||||||||||||
который и применялся для нахождения горизонтальных асимптот.
Обратимся к заданным функциям 1) 3) данного примера. Воспользуемся тем, что графики этих функций уже изображены при решении примера 6. Часть нужных пределов уже указана. Вычисление остальных предоставляем читателю. Из графиков получаем следующие выводы: функция 1) имеет вертикальную
асимптоту |
(ось |
и горизонтальную асимптоту |
(ось |
; функция |
|
2) имеет |
горизонтальную асимптоту |
при этом |
график |
функции на |
|
бесконечностях, колеблясь (принимая как положительные, так и отрицательные
значения), сближается |
с асимптотой – осью |
; третья функция имеет |
вертикальную асимптоту |
и горизонтальную – |
. |
Четвёртая функция |
изучалась в |
школе. График функции, |
называемый тангенсоидой, имеет бесконечное число вертикальных асимптот,
которыми являются прямые |
|
функция терпит разрывы второго рода с |
|
||
бесконечным скачком. |
|
|
|
53 |
|
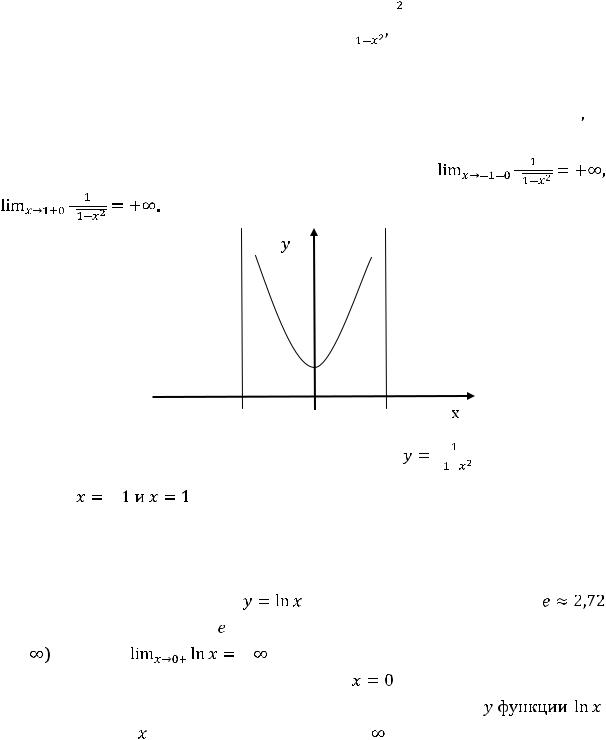
Обратимся к функциям 5) и 6), графики которых уже изображены при решении предыдущего примера. Первая из этих функций имеет вертикальную асимптоту 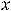

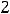 (можно сказать – одностороннюю, см. график) и одну горизонтальную асимптоту
(можно сказать – одностороннюю, см. график) и одну горизонтальную асимптоту 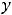

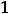 , которую можно назвать двусторонней (пределы при
, которую можно назвать двусторонней (пределы при 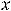
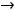

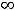 и
и 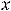
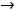
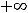 совпадают и равны единице). Функция 6) имеет одну двустороннюю горизонтальную асимптоту
совпадают и равны единице). Функция 6) имеет одну двустороннюю горизонтальную асимптоту 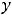


Приступим к исследованию функции 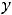

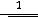 график функции изображён на рисунке 16.
график функции изображён на рисунке 16.
Очевидно, что область определения функции задаётся неравенством 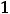

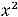
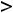
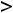
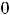
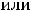
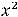
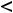
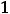 ; таким образом. этой областью является интервал
; таким образом. этой областью является интервал 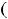

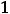
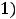 .
.
Концами этого интервала и определяются вертикальные асимптоты.
Односторонние пределы в этих точках таковы:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|||
|
-1 |
|
|
1 |
|
|
|
|
|
|
|
|
Рисунок 16 – График функции |
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
Итак, |
|
есть вертикальные |
асимптоты этой функции; они |
|||||||
|
||||||||||
связаны с границей области определения функции. О горизонтальных и наклонных асимптотах говорить невозможно, так как функция определена на промежутке конечной длины.
Логарифмическая функция |
|
|
с |
основанием |
логарифмов |
|
|
(логарифмы с основанием |
называются |
натуральным) |
определена на |
луче |
|||
(0,+ . Так как |
|
|
, то с левой границей области определения |
||||
|
|
||||||
этой функции связана вертикальная асимптота |
. |
|
|
||||
Выясним наличие наклонных и горизонтальных асимптот |
. |
||||||
Так как аргумент можно устремить только к + |
, то возможны только правая |
||||||
|
54 |
|
|
|
|
||

наклонная |
асимптота. |
|
Вычислим |
коэффициент |
|
|
|
|
|
||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
. При раскрытии неопределённости применили |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
правило |
Лопиталя. |
|
|
Теперь |
вычисляем |
|
|
||||||
|
|
|
|||||||||||
|
|
|
|
|
это означает, что нет ни наклонной, ни горизонтальной |
||||||||
асимптоты.
Функция 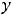

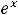 относится к показательным функциям. Она определена и непрерывна на всей числовой оси
относится к показательным функциям. Она определена и непрерывна на всей числовой оси 
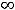
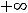
 так как основание
так как основание 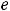
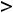
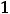 , то она является строго возрастающей на всей области определения. В силу непрерывности отсутствуют вертикальные осаимптоты.
, то она является строго возрастающей на всей области определения. В силу непрерывности отсутствуют вертикальные осаимптоты.
Приступим к нахождению наклонных асимптот. Обратим внимание, что надо рассмотреть обе ситуации: 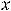
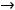

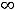
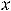
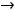
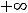
 Для коэффициента
Для коэффициента 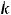 имеем
имеем
следующее: 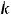

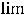
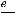



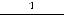

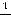

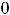 (при вычислении
(при вычислении
пределы использованы символические записи, с которыми читатель должен быть знаком); 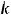

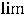
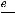

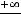

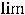
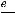

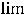
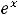

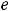
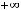

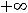 (этот случай означает, что на +
(этот случай означает, что на +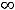 наклонной асимптоты нет). Коэффициент
наклонной асимптоты нет). Коэффициент 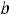
надо вычислять только на (- |
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
||||||
Подставляя найденные |
|
в уравнение |
получаем, что y=0. |
|||||||
Следовательно, ось |
( |
есть горизонтальная асимптота. |
|
|
|
|||||
Функции |
|
называют экспоненциальной и |
часто |
применяют |
||||||
обозначение |
|
её график называют экспонентой. |
Функции |
|
|
и |
||||
имеют многочисленные применения, в том числе и в экономике. Их графики изображены на рисунках 17, 18. Функции являются взаимно обратными.
1
1 |
е |
|
Рисунок 17 – График функции |
Рисунок 18 – График функции |
55
|
|
Функция |
, рассмотренная на интервале |
|
|
|
|
|
|
с областью значений |
||||||
|
|
|
|
|
|
|||||||||||
(- |
|
|
|
|
|
имеет обратную, которой и является функция |
область |
|||||||||
определения последней есть (- |
, а область значений является интервал |
|||||||||||||||
|
|
|
|
|
|
. |
Так |
как функция непрерывна на всей |
числовой оси, то |
|||||||
|
|
|
|
|||||||||||||
вертикальных асимптот нет. Проведём исследование на наличие наклонных
асимптот. Вычислим коэффициент |
при |
|
Это означает, |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что возможны только горизонтальные асимптоты. Вычислим соответствующие
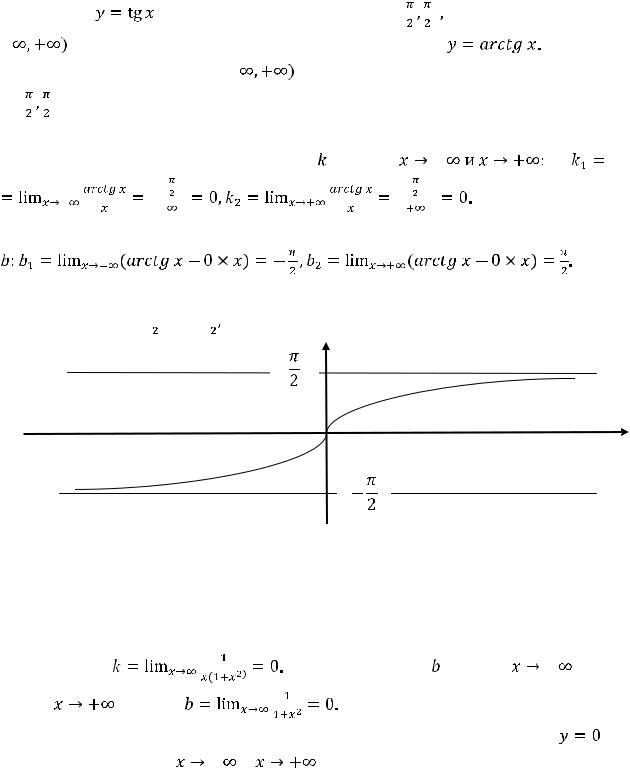
Таким образом, функция 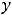

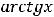 имеет две односторонние горизонтальные асимптоты
имеет две односторонние горизонтальные асимптоты 
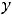


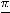 и
и 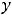

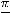 что и изображено ниже на рисунке 19.
что и изображено ниже на рисунке 19.
Рисунок 19 – График функции 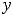

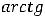
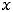
Функция 11) определена на всей числовой оси и непрерывна на ней, так как является частным двух непрерывных функций 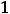
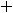
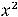
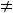
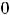
 Следовательно, вертикальных асимптот нет. Исследуем на наличие наклонных асимптот.
Следовательно, вертикальных асимптот нет. Исследуем на наличие наклонных асимптот.
Очевидно, что |
|
|
|
|
|
Для коэффициента (как при |
|
, так |
|
|
|
|
|
|
|
||||
и при |
) имеем |
|
|
|
Таким образом, график функции, |
||||
|
|
|
|||||||
построенный на рисунке 20, |
имеет единую двустороннюю асимптоту |
, |
|||||||
поскольку предела при |
|
и |
|
равны. |
|
|
|||
|
|
|
|
||||||
56
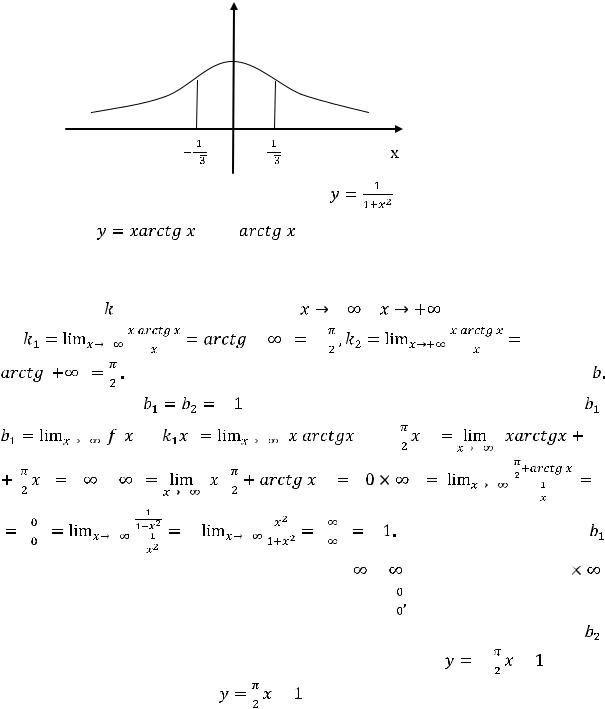
y
1
0
|
Рисунок 20 – График функции |
|
Функция |
(см. |
в задании 10)), очевидно, определена и |
непрерывна на всей числовой оси. Так как функция непрерывна, то вертикальных асимптот нет. Выясним наличие наклонных асимптот. Вычислим
коэффициент |
|
|
|
, рассматривая ситуации |
|
|
|
|
|
|
|
и |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Теперь |
найдём |
соответствующие |
|
коэффициенты |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Оказывается, |
что |
|
|
|
. Покажем, как вычисляется коэффициент : |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
вычислении |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
проведено преобразовании неопределённости |
|
|
|
|
|
|
в неопределённость 0 |
, |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
которая была преобразована в |
неопределённость |
|
к раскрытию последней |
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
применили правило Лопиталя. |
|
Аналогично |
вычисляется |
коэффициент |
. |
|||||||||||||||||||||||||||||
Следовательно, имеется как левосторонняя |
асимптота |
|
|
|
|
|
|
, так |
и |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
правосторонняя асимптота |
|
|
|
|
|
. Примерный график этой функции |
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
изображён на рисунке 21.
57
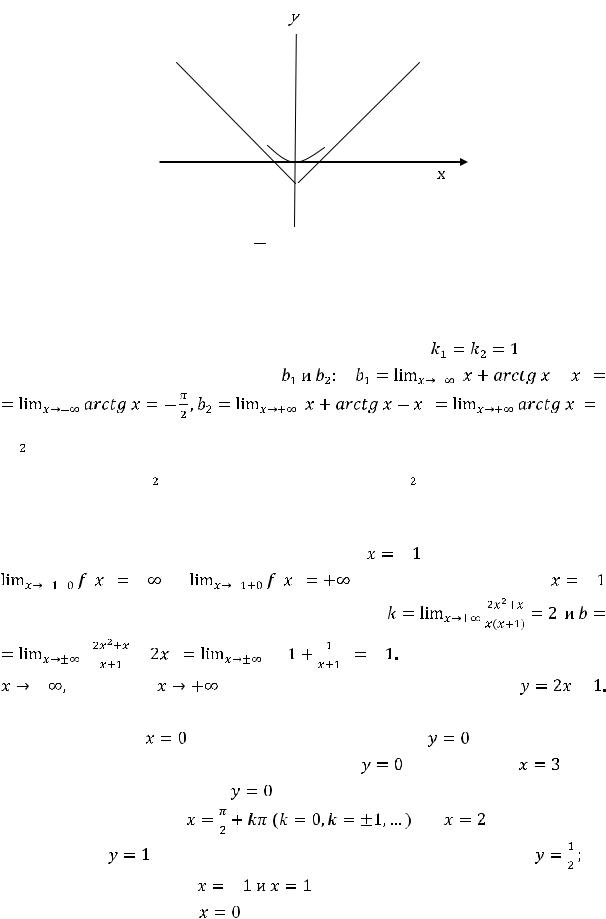
-1 1
-1
Рисунок 21 График функции 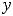

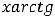
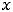
Функция 13) определена и непрерывна на всей числовой оси. Ввиду непрерывности вертикальных асимптот нет. Исследуем функцию на наличие
наклонных асимптот. Нетрудно видеть, что |
|
. Найдём |
||
соответствующие коэффициенты |
|
|
|
|
|
|
|
|
|

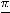 . Таким образом, график функции имеет левостороннюю наклонную
. Таким образом, график функции имеет левостороннюю наклонную
асимптоту 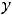

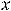

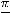 и правостороннюю –
и правостороннюю – 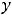

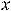
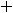
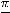 . Наклонные асимптоты кривой параллельны. Предоставляем читателю построить примерный график функции 19).
. Наклонные асимптоты кривой параллельны. Предоставляем читателю построить примерный график функции 19).
Последняя функция не определена в точке |
|
|
|
|
|
. Легко установить, что |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Следовательно, прямая |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
есть вертикальная асимптота этой функции. Далее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, как при |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
так и при |
|
имеется единая наклонная асимптота |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Рекомендуем читателю построить примерный график этой функции. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Ответы: |
1) |
|
|
|
|
|
|
вертикальная |
асимптота, |
|
|
|
|
горизонтальная |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
асимптота; 2) горизонтальная асимптота |
; |
|
3) |
прямая |
|
|
есть |
|||||||||||||||||||||||||||||||||||||||||||
вертикальная |
асимптота, |
а |
|
|
горизонтальная; |
4) |
бесконечное |
число |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
вертикальных асимптот |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 5) |
|
|
|
|
|
вертикальная |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
асимптота, а |
|
|
|
|
|
горизонтальная; |
6) |
|
горизонтальная |
асимптота |
|
|
7) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
вертикальные асимптоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на границе области определения; 8) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
вертикальная |
асимптота |
|
|
|
|
|
; 9) горизонтальная левосторонняя асимптота |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
