
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

В |
случае |
|
|
|
|
|
|
|
|
|
|
|
исходная |
приближённая формула |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
принимает вид |
|
|
|
|
|
|
|
|
|
|
|
. |
|
Для вычисления |
надо |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
взять |
|
|
и |
|
|
|
(тогда |
= |
|
|
|
|
|
|
|
, |
что соответствует |
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответы: 1) 
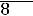
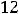
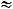
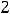
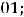 2)
2) 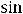
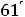
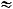
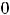
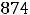
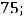 3)
3) 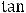
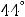
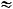
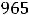

Модуль 4. Функции многих переменных
Пример 1. Указать области определения следующих функций двух переменных:
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
2) |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Решение. Область определения первой функции задаётся условием |
|
|
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
. Очевидно, что такое неравенство |
|
задаёт на |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
плоскости |
|
круг радиуса |
с центром в начале координат. |
В область |
|||||||||||||||||||||||||||||||||
определения включается и граница этого круга – окружность |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
радиуса |
|
|
|
с центром в точке (0,0). Отметим, что графиком функции является |
|||||||||||||||||||||||||||||||||
полусфера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Область определения второй функции задаётся условием |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
или |
|
|
|
|
|
|
, т.е. представляет собой круг без его границы – окружности |
||||||||||||||||||||||||||||||
радиуса |
|
|
|
с центром в начале координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Третья |
функция определена |
во всех очках плоскости |
, для которых |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
. Следовательно, функция определена во всех |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
точках плоскости, кроме точек упоминавшейся окружности |
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||
Функция 4) определена в точках плоскости, которые удовлетворяют
неравенству |
|
|
или |
. Область |
определения |
|
|||||
представляет собой внешность упоминавшегося круга радиуса |
с центром в |
||||
начале координат с включением точек окружности. |
|
|
|||
Ответы: 1) круг радиуса |
с центром в начале координат ( |
|
|||
с включением его границы – окружности; 2) открытый круг |
, круг |
||||
без его границы – окружности; 3) плоскость без точек окружности |
; |
||||
4) задаётся неравенством |
|
|
|
||
|
|
|
84 |
|
|

Пример 2. Найти уравнения линий уровня следующих функций: 1)
|
|
|
2) |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Понятие линии уровня функции двух переменных |
|||||||||||
подробно описано на стр. 82 (задание 16). |
|
|
|
|
|
||||||
Линии уровня первой функции задаются |
уравнением |
|
|
||||||||
|
|||||||||||
где |
. При |
плоскость |
не будет пересекать поверхность |
||||||||
(параболоид), которую задаёт эта функция. |
При |
|
это уравнение задаёт |
||||||||
окружность с центром в точке (2, -1) и радиусом |
|
. Таким образом, линии |
|||||||||
|
|||||||||||
уровня этой функции есть концентрические окружности с указанным центром и
радиусом. При |
получаем вырожденную линию уровня – |
точку (2, |
-1), |
|||
соответствующую наименьшему значению функции |
. |
|
|
|||
График функции представляет поверхность, называемую параболоидом. |
|
|||||
Линии уровня |
функции |
|
, графиком которой является поверхность, |
|||
называемая гиперболическим параболоидом, задаются уравнением |
При |
|||||
линией уровня будет пара пересекающихся прямых |
. |
При |
||||
они имеют вид |
|
, т.е. линиями уровня являются гиперболы. |
При |
|||
|
||||||
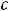
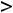
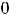 ветви любой такой гиперболы лежат в первой и третьей четвертях, а при - во второй и четвёртой. Линии уровня третьей функции определяются
ветви любой такой гиперболы лежат в первой и третьей четвертях, а при - во второй и четвёртой. Линии уровня третьей функции определяются
уравнением |
|
|
|
|
|
, т.е. представляют собой на плоскости прямые, |
||||||||
|
|
|
|
|||||||||||
проходящие через начало координат, исключая прямую |
(ось |
, в точках |
||||||||||||
которой функция не определена. |
|
|
|
|
|
|
|
|
||||||
Ответы: 1) |
|
|
|
; 2) |
|
|
|
|
, |
|
; 3) |
. |
||
|
|
|
|
|||||||||||
Пример 3. |
Вычислить |
следующие |
пределы, если |
они |
существуют: |
|||||||||
1) |
|
|
; 2) |
3) |
|
|
; 4) |
|
|
. |
|
|||
|
|
|
|
|
|
|||||||||
Решение. Первая функция определена на всей плоскости. Пользуясь
теоремой о пределе суммы, получим, что |
|
|
|
Вторая функция (показательно-степенная) существует при |
и |
||
произвольном . Тогда, если |
|
любое действительное число, |
то |
|
|||
Это можно показать на основании определения предела на «языке последовательностей». Следовательно, 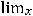
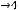
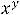

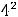

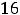

85

Вычисление пределов функции двух переменных является более сложной задачей по сравнению с вычислением предела функции одной переменной. Это
связано с тем, что переменная точка |
из области определения функции |
может стремиться к предельной точке |
области определения по |
различным направлениям, а таких направлений – бесконечное множество. Для функций одной переменной точка 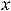 может стремиться к предельной точке
может стремиться к предельной точке 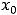 на числовой прямой только по следующим направлениям: только слева, только справа, слева и справа.
на числовой прямой только по следующим направлениям: только слева, только справа, слева и справа.
Предел функции двух переменных в точке 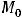 будет существовать только тогда, когда многочисленные значения пределов по всем возможным направлениям совпадут между собой.
будет существовать только тогда, когда многочисленные значения пределов по всем возможным направлениям совпадут между собой.
|
Функция |
|
определена всюду |
на плоскости, кроме |
|
прямой |
. |
|||||||||
|
||||||||||||||||
Функция в точке |
|
не определена, но о наличии предела в ней можно |
||||||||||||||
говорить. Выберем направление движения к (0,0) по прямым |
|
|
(при таком |
|||||||||||||
движении при |
|
и переменная |
. Тогда |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
. При различных значениях углового коэффициента |
прямой |
|||||||||||||
|
|
получаем различные значения предела. Данный предел не существует. |
||||||||||||||
|
Функция |
|
|
определена всюду на плоскости, кроме точки (0,0). Будем |
||||||||||||
|
|
|||||||||||||||
приближаться к (0,0) по прямым |
Тогда |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||||
|
Данный предел не существует, поскольку при различных |
получим разные |
||||||||||||||
значения предела. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ответы: 1)13; 2) 16; 3) не существует; 4) не существует. |
|
|
|
|
|
|
|
||||||||
Пример 4. Найти частные и полные приращения функций: 1) 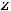

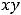
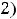
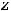

. |
|
|
|
|
|
|
|
|
|
|
Решение. Частным приращением |
|
функции |
|
по переменной |
||||||
называется величина |
|
|
а частным приращением по |
|||||||
|
|
|||||||||
– величина |
|
|
|
|
|
|
Полным |
приращением |
называется |
|
|
|
|
|
|||||||
величина |
|
|
|
|
, т.е. разность |
между |
значениями |
|||
|
|
|
||||||||
функций в точках |
и |
|
, при |
этом |
обе точки должны |
|||||
принадлежать области определения функции. Для первой функции имеем следующее:
86

Найдём все приращения второй функции:
У второй функции получилось, что полное приращение функции равно сумме её частных приращений. Однако в общем случае такого равенства нет, т.е. 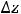
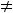
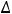
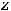
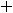
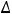
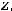 Это мы видим при сравнении приращений первой функции.
Это мы видим при сравнении приращений первой функции.
Ответы: 1) 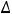
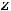

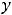
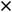
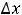
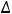
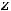

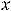
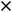
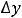
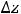

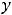
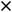
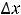
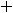
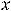
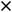
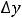
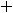
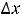
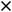
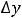
 2)
2)
Пример 5. Исследовать на непрерывность функции примера 4.
Решение. Воспользуемся разностным условием непрерывности. Функция
называется непрерывной в точке |
если выполняется |
равенство |
|
Полные приращения этих функций найдены в примере 4. Воспользовавшись этим, получим следующее:
Таким образом, обе функции, определённые на всей плоскости, непрерывны в каждой точке плоскости. Графики этих функций представляют собой сплошные, не расслаивающиеся поверхности. Уже упоминалось, что первая поверхность называется гиперболическим параболоидом. Она имеет вид седла. Вторая поверхность есть параболоид вращения (сечениями в координатных плоскостях 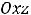
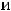
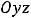 являются параболы
являются параболы 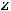

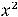
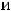
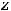

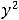 ).
).
Ответ: Обе функции непрерывны на всей плоскости.
Пример 6. Указать точки разрыва функций 1) |
|
; 2) |
|
|
; |
|
|
|
|
|
|||
3) 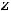

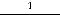 .
.
Решение: Первая функция имеет единственную точку разрыва 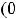
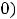 – начало координат, а вторая разрывна в точках целой линии прямой
– начало координат, а вторая разрывна в точках целой линии прямой 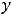

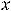 . В обоих случаях функции в точках разрыва обращаются в бесконечность.
. В обоих случаях функции в точках разрыва обращаются в бесконечность.
87

Третья функция терпит разрыв в каждой точке окружности 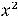
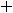
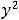

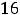 , при приближении к точкам этой линии значения функции стремятся к бесконечности.
, при приближении к точкам этой линии значения функции стремятся к бесконечности.
Ответ: 1) |
2) точки прямой |
; 3) точки окружности |
. |
||
Пример 7. |
Найти частные производные |
и |
функций примера 4 на |
||
основании определения частных производных.
Решение: Частные производные первого порядка функции
определяются равенствами |
|
|
|
, |
|
|
|
|
. Воспользуемся |
|||
|
|
|||||||||||
ещё тем, что частные приращения этих функций вычислены в примере 4. |
||||||||||||
Для функции |
. |
имеем |
|
|
, |
|||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для функции |
имеем |
|
|
|
|
|
||||||
|
|
|
|
|
||||||||
, |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На основании этих результатов можно заметить правило: при вычислении частной производной по одной переменной на другую переменную надо смотреть как на постоянную величину и применять правила вычисления производной функции одной переменной и таблицу производных основных
элементарных функций. |
|
|
|
|
|
|
|
||
|
Ответ: 1) |
; 2) |
. |
|
|
||||
|
Пример 8. Найти частные производные первого порядка следующих |
||||||||
функций: |
|
|
|
|
|
|
|
||
5) |
|
. |
|
|
2) |
|
; 3) |
; 4) |
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Решение: Будем руководствоваться правилом, сформулированным при решении примера 7.
Для соответствующих функций получим следующие результаты:
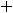
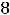

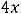
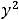
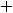
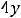
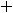
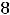 ,
,

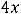
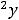
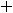
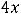

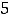 ;
;
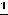 ;
;
, |
; |
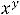
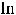
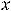 ;
;
88

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
Ответы: 1) |
|
|
|
|
|
; 2) |
|
|
; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
; 4) |
|
|
; |
5) |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||



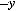
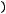 .
.
Пример 9. Вычислить частные производные первого порядка сложных
функций |
1) |
|
|
; 2) |
; |
3) |
; |
4) |
; |
5) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: Все функции примера имеют вид |
|
, т.е. являются |
|||||||
композициями |
функций |
|
|
; переменная |
является |
||||
промежуточным |
аргументом. |
Тогда |
частные производные |
вычисляются по |
|||||
формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где |
есть обычная производная |
. |
|
|||||||||||||||||||||
|
Функцию |
|
1) можно представить |
в виде |
|
|
|
, где |
|
. Тогда |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
Вторая функция представима в виде |
|
, где |
|
. По аналогии с |
|||||||||||||||||||||||||||||||||||||
предыдущими действиями получим, что |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||
|
Функция 3) представляется в виде |
|
|
|
, где |
. |
Тогда |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Для функции 4) имеем |
, |
где |
|
|
|
. Так как |
|
|
|
|
|
|
|
|
и |
||||||||||||||||||||||||||
, |
|
|
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||
|
Последняя функция представима в виде |
|
|
|
|
|
|
, где |
|
|
|
. Так |
как |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
. |
|
|
|
|
|
|
|
и |
|
|
|
|
, |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1) |
|
|
|
|
|
; |
|
|
2) |
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 10. Найти производную функции |
в точке |
|
|
в |
|||||||||||||||||||||||||||||||||||||
направлении вектора |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
89

Решение: |
Производная |
|
функции |
в точке |
по |
||
|
|||||||
направлению |
вектора |
|
вычисляется по |
формуле |
|
|
|
|
|
|
|||||
, где |
есть угол, который образует вектор |
с осью , а |
– с осью |
||||
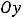 . Из аналитической геометрии известно, что направляющие косинусы вектора
. Из аналитической геометрии известно, что направляющие косинусы вектора
следующим |
образом |
выражаются |
через |
его |
координаты: |
|||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим по этим равенствам направляющие косинусы заданного вектора
. Так как |
|
|
|
|
, то |
|
, |
|
. |
|
|
|
|
|
|
|
|
||||
Найдём значения частных производных данной функции в точке |
: |
|||||||||
|
. |
|
|
|
|
|
|
|
|
|
Подставляя все найденные значения в выписанную формулу нахождения 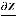 ,
,
получим |
|
|
|
|
. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||
Ответ: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
Пример 11. Найти градиент функции |
в точке |
. |
|||||||||
Решение: Градиентом функции |
в точке |
называется |
|||||||||
двумерный вектор |
|
|
с координатами |
: |
. |
||||||
Отметим основные свойства этого вектора: 1) градиент перпендикулярен к линии уровня функции, проходящей через точку 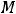 ; 2) в направлении градиента функция возрастает; 3)
; 2) в направлении градиента функция возрастает; 3) 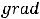
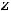 в данной точке характеризует направление и величину максимальной скорости изменения функции в этой точке, при этом
в данной точке характеризует направление и величину максимальной скорости изменения функции в этой точке, при этом
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что градиент заданной |
функции |
в любой |
точке |
есть |
||||
вектор |
|
. Тогда |
в точке |
|
это будет |
вектор |
||
|
или |
, |
где |
– стандартный базис |
||||
двумерного пространства . |
|
|
|
Рекомендуем читателю построить этот вектор и линию уровня функции, |
|
проходящую через точку |
. |
|
|
Ответ: |
. |
|
Пример 12. Вычислить все частные производные второго порядка функций |
|
1) |
, 2) |
. |
|
|
90 |

Решение: Частные |
производные |
вообще говоря, являются снова |
функциями переменных |
. Дифференцируя каждую из них как по , так и по |
|
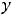 , получим четыре частные производные второго порядка. В обозначениях это
, получим четыре частные производные второго порядка. В обозначениях это
будет выглядеть так: |
|
|
|
. |
|
При этом производные |
и |
называются смешанными. |
В случае их |
||
непрерывности они будут равны. |
|
|
|
||
Для первой |
функции |
|
, а |
|
. Тогда на |
основании приведенных |
формул |
|
|
, |
|
. |
Очевидно, что имеется равенство |
. |
|
||
Первые частные производные второй функции вычислены в примере 9, при
этом |
. Для вычисления вторых производных |
|
надо применять правило вычисления производных от произведения |
функций. |
Тогда |
, |
|
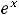

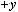
 .
.
Так как смешанные производные непрерывны, то снова имеем равенство
. |
|
Ответы: 1) |
; |
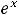

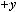
 .
.
Пример 13. Исследовать на экстремум функции 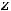

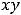
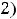
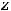

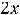
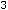
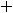
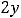
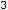

Решение. Определение экстремума (минимума или максимума) для функции двух переменных аналогично определению экстремума функции одной
переменной. Под окрестностью точки |
|
|
будем понимать открытый круг |
|||
с центром |
в |
некоторого радиуса |
, т.е. множество точек |
плоскости, |
||
удовлетворяющих неравенству |
|
|
|
|
||
|
|
|
|
|||
Если |
есть точка экстремума дифференцируемой функции |
, т.е. |
||||
функции, имеющей непрерывные частные производные, то выполняются
равенства |
или |
|
91 |

Точки 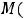
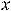
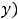 , в которых выполняются равенства
, в которых выполняются равенства 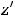

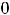
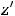

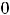 , называются критическими или стационарными. Такие точки подозрительны на экстремум, однако его может и не быть. То же самое имели для функции одной переменной.
, называются критическими или стационарными. Такие точки подозрительны на экстремум, однако его может и не быть. То же самое имели для функции одной переменной.
У функции |
частные производные первого порядка таковы: |
|
|
. Единственной стационарной |
точкой является точка |
. |
|
Экстремума в этой точке нет, т.к. |
а в любой окрестности точки |
|
|
функция принимает как положительные, так и отрицательные значения. |
|
||
Теперь исследуем вторую функцию, определённую на всей плоскости. Частные производные первого порядка таковы: 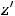

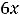
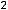

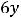
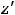

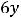
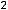

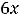 т.е. также существует на всей плоскости. Тогда критические точки являются решениями системы
т.е. также существует на всей плоскости. Тогда критические точки являются решениями системы
Легко установить, что есть две критические точки, а именно 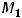
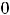
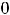
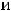
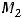
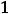
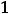
 Остаётся выяснить, являются ли они точками экстремума для функции двух переменных.
Остаётся выяснить, являются ли они точками экстремума для функции двух переменных.
Пусть функция непрерывна и имеет непрерывные частные производные первого второго порядков в некоторой окрестности стационарной точки 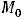
 Введём обозначения:
Введём обозначения: 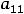

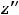
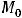
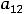

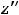
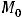
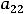

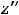
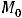

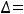
Справедливо утверждение: 1) если 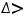
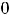 , то в стационарной точке
, то в стационарной точке 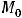 будет экстремум, причём максимум при
будет экстремум, причём максимум при 
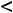
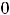 и минимум при
и минимум при 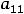
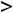
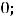 2) если
2) если 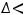
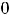 , то экстремума нет.
, то экстремума нет.
Применим это утверждение. Найдём частные производные второго порядка:
Для точки |
|
|
имеем |
: |
|
|
|
|
. Тогда |
|
|
|
|
|||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
. Следовательно, в этой точке экстремума нет. |
||||||||||
|
|
|
|
|||||||||||||
Для точки |
|
|
|
|
|
|
|
|
. Тогда |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
. |
В этой |
точке имеется экстремум и так как |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
то минимум. При этом |
. |
|
|
|
|
|||||||
Ответы: 1) функция экстремума не имеет; 2) в точке (1, 1) функция имеет
минимум, |
. |
|
92 |

Пример 14. Найти дифференциалы функций в данных точках при заданных приращениях аргументов: 1) 

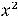
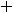
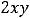
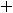
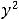
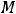
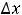

Решение. В случае дифференцируемой функции двух переменных её
дифференциалом |
|
|
|
называется |
выражение |
|
|
где |
|||||||||||||||||
дифференциалы |
|
|
|
аргументов |
функции есть их |
приращения |
т.е. |
||||||||||||||||||
|
|
|
|
|
Таким образом, дифференциал зависит от значений |
|
|||||||||||||||||||
|
Так как у первой функции |
|
то её дифференциал в |
||||||||||||||||||||||
любой точке |
|
|
|
имеет вид |
|
В |
точке |
||||||||||||||||||
|
|
|
|
будем иметь |
Положив |
в последнем равенстве |
|||||||||||||||||||
|
|
|
|
|
|
получим |
|
|
|
|
|||||||||||||||
|
Частные производные первого порядка второй функции таковы: |
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим это равенство координаты данной |
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
точки, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Придав дифференциалам аргументов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
заданные значения |
, получаем |
окончательный |
ответ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: 1) |
; 2) |
Пример 15. Найти приближённое значение числа 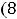
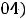
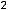
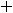
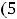
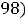
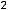
 Решение. Для дифференцируемой функции двух переменных справедливо
Решение. Для дифференцируемой функции двух переменных справедливо
приближённое равенство 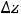
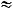
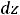 , из которого на основании определений полного приращения функции и её дифференциала следует приближённое
, из которого на основании определений полного приращения функции и её дифференциала следует приближённое
равенство |
|
|
|
|
|
|
|
|
|
которое тем |
||||||||
точнее, чем меньше |
– приращения аргументов функции. |
|||||||||||||||||
|
|
В данном примере за функцию надо взять |
|
|
Так как |
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
то теоретическое приближённое равенство примет вид |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что в |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
этом равенстве надо |
положить |
|
|
Значения |
||||||||||||||
|
|
|
|
|
|
|
|
стоящие в правой части |
последнего равенства, |
|||||||||
93
