
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание

вычисляется легко, если положить 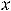

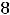
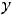

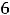 (тогда
(тогда 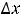

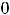
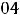 а
а 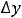


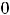
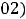 .
.
Действительно 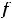
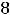
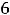

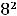
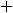
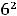

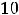
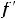
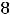
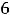

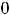
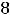
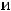
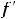
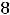
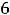

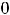
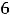
 Подставляя все аргументы и указанные их приращения в выписанное
Подставляя все аргументы и указанные их приращения в выписанное
приближённое равенство для этой функции, получим
Ответ: 10,02.
Модуль 5. Интегральное исчисление
Пример 1. Выяснить, какая из функций 1) |
является |
|||
первообразной функции |
|
|
|
|
|
|
|
|
|
Решение. Функция |
есть первообразная для функции |
на некотором |
||
промежутке, если для всех точек 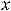 этого промежутка выполняется равенство
этого промежутка выполняется равенство
Ясно, что такой функцией является функция 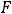
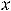

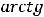
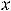
 Для этого читателю надо только вспомнить таблицу производных основных элементарных функций и определение дифференциала.
Для этого читателю надо только вспомнить таблицу производных основных элементарных функций и определение дифференциала.
Напомним, что |
первообразной заданной функции будет и функция |
||
где |
|
|
произвольное постоянное число. |
|
|
||
Ответ: |
|
|
|
Пример 2. Вычислить неопределённый интеграл
|
Решение. Надо воспользоваться |
свойствами |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
и таблицей интегралов |
|
основных |
|||||||||||
элементарных функций. В результате получим, что |
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 3. Вычислить следующие неопределённые |
интегралы: |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
Решение. Если в неопределённом интеграле |
|
|
сделать подстановку |
||||||||||||||||||
|
|
(тогда |
|
то |
получим |
|
|
формулу |
||||||||||||||
|
|
|
|
|
|
|
|
|
94 |
|
|
|
|
|
|
|
|
|
|
|
|
|
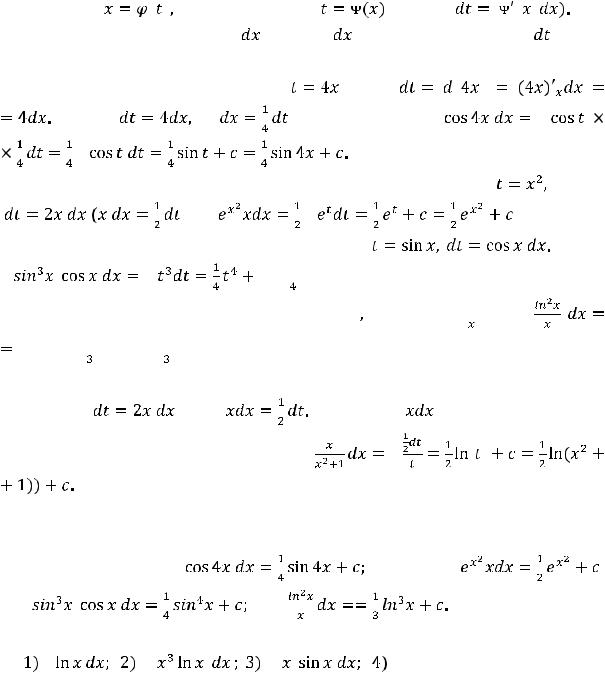
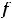
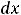

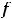
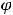
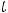
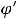
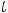
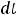
 В этом равенстве интеграл, стоящий справа, часто оказывается табличным; тогда получим ответ, если возвратимся к прежней переменной
В этом равенстве интеграл, стоящий справа, часто оказывается табличным; тогда получим ответ, если возвратимся к прежней переменной 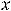 . В противном случае придётся проводить некоторые преобразования подынтегральной функции от переменной
. В противном случае придётся проводить некоторые преобразования подынтегральной функции от переменной 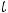 , чтобы получить табличные интегралы.
, чтобы получить табличные интегралы.
Этот метод называется методом подстановки или методом замены переменной. При замене переменной часто более удобной оказывается не
подстановка |
|
а подстановка |
|
|
(тогда |
В |
||||||||||||||
исходном интеграле участвует |
|
и тогда |
надо суметь связать с |
. Такая |
||||||||||||||||
связь легко обнаружится в заданиях этого примера. |
|
|||||||||||||||||||
|
В задании 1) сделаем подстановку |
. Тогда |
|
|||||||||||||||||
|
|
Так как |
|
то |
|
|
|
и, следовательно, |
|
|||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для вычисления |
|
интеграла |
|
2) применим подстановку |
тогда |
||||||||||||||
|
|
|
|
|
|
|
|
) и |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
В третьем интеграле делаем |
подстановку |
Тогда |
|||||||||||||||||
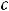

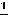
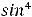
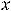
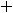
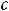 .
.
В случае 4) сделаем подстановку 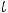

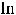
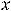 тогда
тогда 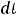

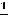
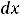 и
и
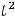
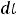

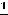
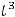
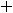
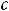

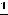
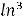
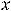
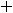
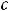 .
.
Для вычисления последнего интеграла применим подстановку 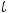

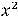
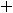
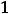 ,
,
при этом |
или |
|
Так как |
стоит в числителе |
|
подынтегрального выражения, то
Отметим, что все интегралы свелись к табличным. Упрощать новые подынтегральные функции в этих заданиях не пришлось.
Ответы: |
1) |
|
|
|
2) |
|
; |
||||
|
|
||||||||||
3) |
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4. Вычислить следующие интегралы:
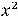
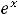
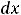 .
.
95

Решение. |
Если |
|
|
|
|
дифференцируемые |
функции, |
то |
|
|
|
||||||
справедливо |
равенство |
|
|
|
|
называемое |
формулой |
|
|
|
|
|
|||||
интегрирования по частям. |
|
|
|
|
|
|
|
|
При применении этой формулы надо увидеть, какую функцию взять за |
и |
|||||||
какое выражение принять за |
При применении этого |
метода надо |
||||||
руководствоваться правилом: интеграл |
|
|
|
|
, стоящий справа в этом равенстве, |
|||
должен быть или табличным или легко вычислимым. Часто приходится снова вычислять по частям.
При вычислении таких интегралов нужные обозначения обычно пишут в квадратных скобках.

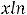
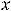

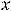
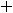
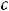 ;
;
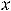

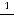
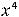
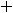
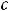 ;
;
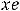
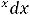 .
.
Может показаться, что при вычислении интеграла 4) выбраны неверные обозначения. Однако это не так. Полученный справа интеграл снова берём по
частям: |
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
||||
Итак, для интеграла |
4) получаем окончательный ответ: |
||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что в квадратных скобках рядом с функцией |
записывался её |
||||||||
дифференциал, а функцию |
вычисляли путём интегрирования выражения для |
||||||||
, при этом постоянную |
не писали (полагали |
), что не изменит ответа |
|||||||
(проверьте это). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
Пример |
5. |
|
Найти |
определённые |
интегралы |
||||||||||
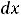 .
.
96

Решение. Для непрерывной на отрезке |
функции справедливо равенство |
|||||
|
|
|
где |
есть любая первообразная подынтегральной |
||
|
|
|
||||
функции |
. Равенство называют |
основной формулой |
интегрального |
|||
исчисления, а также формулой Ньютона-Лейбница. |
|
|||||
Известно, что у непрерывной на |
функции существует её первообразная; |
|||||
при этом первообразная также является непрерывной на отрезке |
функцией. |
|||||
Основная формула означает, что определённый интеграл от непрерывной функции по отрезку 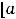
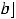 есть приращение её первообразной по этому отрезку. Поэтому формула является простым и удобным способом вычисления определённых интегралов. При вычислении интегралов от конкретных функций правую часть
есть приращение её первообразной по этому отрезку. Поэтому формула является простым и удобным способом вычисления определённых интегралов. При вычислении интегралов от конкретных функций правую часть 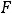
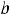

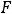
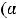
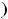 обычно обозначают символ
обычно обозначают символ 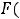
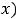
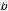

Так как все функции примера непрерывны и их первообразные имеются в таблице неопределённых интегралов, то получаем следующие результаты:
Ответы: 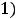
Пример 6. Найти площади плоских фигур, ограниченных кривыми, заданными следующими парами алгебраических уравнений:
Решение. Площадь фигуры, расположенной между кривыми, вычисляется по
формуле |
|
|
|
|
|
|
|
|
|
|
|
где пределы интегрирования |
есть проекции точек пересечения кривых |
||||
на ось |
, рассматриваемые в |
порядке возрастания |
. Под знаком |
||
интеграла первой пишется функция, график которой лежит на отрезке выше.
В обоих случаях сначала надо получить функции, т.е. разрешить уравнения относительно переменной 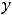 . Очевидно, что в первом случае этими функциями будут
. Очевидно, что в первом случае этими функциями будут 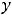

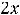
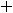
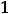
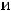
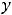

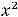

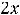

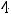 , а во втором -
, а во втором - 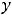

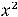

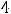
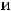
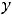

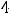

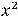 .
.
Приступим к нахождению площади первой фигуры. Решив систему уравнений
97

найдём точки |
|
|
|
|
|
пересечения кривых. |
Из уравнения |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
получаем |
|
|
|
|
|
|
. Это и есть пределы |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
интегрирования ( |
|
|
нижний предел, |
|
|
– |
|
верхний). Обычно строят чертёж. |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
Тогда находят |
|
|
и |
: |
|
|
|
|
|
|
|
|
. Точками пересечения кривых (прямой и |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
параболы) будут |
|
точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
Читателю рекомендуем |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
построить чертёж. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Очевидно, |
что на отрезке [-1, 5] прямая |
|
|
|
|
|
лежит выше параболы |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

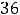 .
.
Для нахождения площади второй фигуры надо решить систему уравнений
Из уравнения |
|
|
|
|
|
|
|
или |
|
|
получаем, что |
|
|
. |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||
Точками пересечения кривых (парабол) |
будут |
|
|
|
|
|
|
Обе лежат |
|||||||||||||||||
|
|
||||||||||||||||||||||||
на оси абсцисс. И в этом случае рекомендуем читателю сделать чертёж. |
|||||||||||||||||||||||||
Так как график параболы |
|
|
|
|
лежит на отрезке [-2, 2] выше графика |
||||||||||||||||||||
|
|||||||||||||||||||||||||
параболы |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

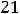
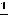 .
.
Ответы: 
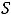

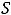

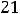
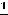 .
.
Пример 7. Исследовать на сходимость следующие несобственные интегралы
первого рода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
Решение. |
Определение несобственного |
интеграла |
вида |
было |
||||||
приведено в |
задании 22 на стр. 17 там |
же указан |
способ |
его вычисления. |
||||||
Применяя этот способ к заданиям этого примера, получим следующее:
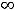

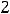

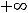 .
.
98
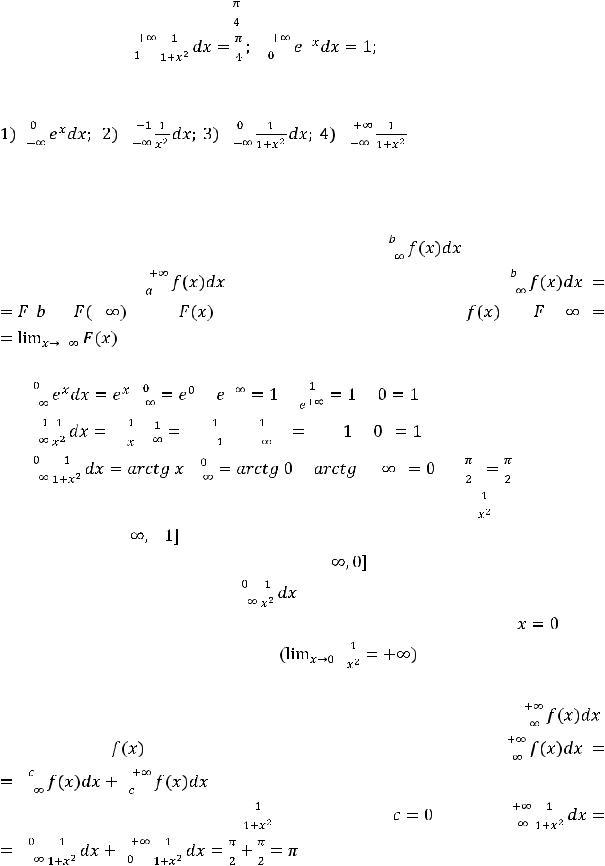
Проведённые вычисления показывают, что первые два интеграла сходятся, а
третий |
|
расходится. При этом найдены |
значения первых двух интегралов. |
||||||||
|
|||||||||||
Соответственно это есть числа |
|
|
|
и 1. |
|
||||||
|
|
|
|||||||||
Ответы: 1) |
|
|
|
|
|
|
2) несобственный интеграл; |
||||
|
|
|
|
|
|
|
|||||
|
|
||||||||||
3) расходится.
Пример 8. Исследовать на сходимость следующие несобственные интегралы:
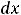 .
.
Решение. Все интегралы являются несобственными интегралами первого рода. Промежутки интегрирования являются бесконечными, а подынтегральная
функция на соответствующем промежутке является непрерывной. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Первые три являются интегралами вида |
|
|
. |
|
По |
|
|
|
аналогии с |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегралами вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, их |
можно |
|
вычислять по формуле |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
где |
|
|
|
|
|
|
|
|
|
|
есть |
|
первообразная |
функции |
|
|
|
|
|
|
|
и |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя эту формулу, получим следующие результаты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Сделаем замечание по поводу интеграла 2). Здесь функция |
|
|
интегрируется |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
по промежутку (- |
|
|
|
|
|
|
|
, на котором она непрерывна. Если для этой же функции |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
промежутком интегрирования взять луч (- |
|
|
|
, то получим уже совершенно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
иной несобственный интеграл |
|
|
|
|
|
|
|
|
. Промежутком интегрирования является |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
бесконечный промежуток и, кроме того, функция на правом конце |
|
|
|
|
|
|
|
|
|
этого |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
промежутка |
|
|
имеет |
особенность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
К его |
вычислению |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
обобщённую формулу Ньютона-Лейбница применять нельзя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Интеграл 4) есть несобственный интеграл первого рода вида |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если функция |
|
|
непрерывна, то он определяется равенством |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где с |
|
|
|
любая точка на числовой оси. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
В силу |
чётности функции |
|
|
|
|
|
|
можно |
взять |
. |
|
Тогда |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
Первый |
|
интеграл |
|
справа в этом |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

равенстве был только что вычислен в задании 3), а второй вычисляется по аналогии с интегралом 1) примера 7.
Ответы: 1) 
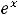
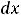

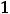 ; 2)
; 2) 
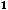
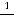
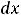

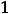 ; 3)
; 3) 
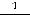
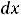

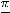 ; 4)
; 4) 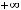
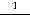
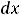 =
=

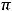 (все интегралы сходятся).
(все интегралы сходятся).
Пример 9. Исследовать на сходимость несобственные интегралы второго
рода 1) |
|
|
|
; 2) |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Решение. Пусть функция определена на конечном промежутке |
, но не |
|||||||||
ограничена на нём. Будем считать, что имеется особенность только в точке 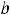 ,
,
т.е. |
|
|
|
|
. Тогда несобственный интеграл второго рода |
|||||
определяется равенством |
|
|
, при этом на |
|||||||
|
|
|||||||||
отрезке |
|
|
функцию |
будем предполагать непрерывной. Тогда к |
||||||
|
|
|||||||||
|
|
|
|
|
||||||
вычислению |
интеграла |
можно применить формулу Ньютона- |
||||||||
Лейбница. |
|
|
|
|
|
|
|
|
||
Если выписанный предел справа существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Функция 1) имеет особенность только в точке |
|
. Тогда |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. этот интеграл сходится и |
его значение |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
равно 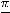 . При вычислении предела воспользовались непрерывностью функции
. При вычислении предела воспользовались непрерывностью функции
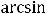
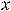 .
.
Функция 2) также имеет особенность только на правом конце промежутка,
т.е. в точке |
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, т.е. интеграл расходится. |
||||||||||
|
|
|
|
|
|
||||||||||||||||
Ответы: 1) |
|
|
|
|
|
|
(сходится); 2) расходится. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
Пример 10. Исследовать на сходимость несобственные интегралы второго
рода 1) |
|
|
|
; 2) |
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Несобственный интеграл второго рода по |
промежутку |
с |
||||||||||
особенностью |
|
функции |
только в точке |
определяется |
|||||||||
равенством |
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
100 |
|
|
||
