
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Множества и отображения
- •Модуль 2. Пределы и непрерывность
- •Модуль 3. Производная и дифференциал
- •Модуль 4. Функции многих переменных
- •Модуль 5. Интегральное исчисление
- •Модуль 6. Дифференциальные уравнения
- •Модуль 7. Числовые и функциональные ряды
- •Библиографический список
- •Содержание


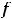
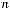
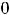

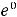

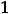 . Таким образом, разложение функции
. Таким образом, разложение функции 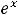 в ряд Маклорена имеет следующий вид:
в ряд Маклорена имеет следующий вид: 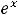

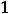
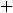
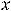
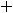
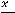
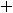
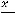
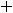
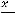
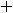
 . Искомым членом является
. Искомым членом является
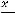 или
или 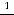
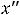 т.е. имеем ответ 1).
т.е. имеем ответ 1).
Модуль 1. Множества и отображения
Пример 1. Найти объединение конечных множеств 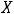

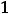
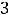
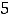
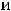
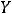

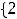
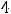
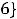 . Решение. Согласно определению объединения множеств (см. задание 1 текстовых заданий с решением) таковым множеством будет
. Решение. Согласно определению объединения множеств (см. задание 1 текстовых заданий с решением) таковым множеством будет 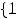
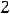
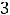
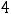
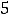
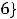 . В него
. В него
входят все элементы обоих исходных множеств.
Ответ: объединением заданных множеств является множество {1,2,3,4,5,6}. Пример 2. Указать объединение конечных множеств 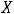

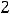
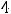
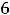
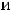
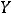


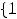
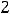
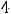
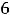
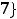 .
.
Решение. Объединением этих множеств будет множество {1,2,4,6,7}, т.е. объединение совпало множеством 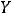
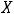
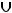
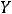

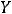

Ответ: {1,2,4,6,7}.
Пример 3. Найти объединение множеств 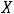

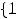
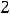
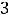
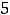
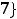 и
и 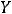

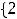
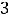
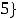 . Решение. Объединением
. Решение. Объединением 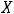
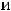
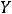 будет множество {1,2,3,5,7}, т.е. объединение
будет множество {1,2,3,5,7}, т.е. объединение
совпало с множеством 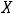
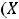
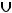
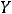

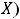 .
.
|
Ответ: {1,2,3,5,7}. |
|
|
|
|
|
|
|
||
|
Пример 4. Указать объединение следующих множеств: |
|
|
и |
||||||
|
||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Очевидно, |
что |
. Действительно, все |
элементы |
|||||
множеств |
принадлежат полуотрезку [0,15), при |
этом общие элементы |
||||||||
(точки множества (5,10]) входят один раз. |
|
|
|
|
|
|
||||
|
Ответ: полуотрезок [0,15). |
|
|
|
|
|
|
|||
|
Пример |
5. Найти |
объединение |
множеств: |
|
интервала |
(1,10) и |
|||
|
|
|||||||||
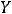
 интервала (7,12).
интервала (7,12).
Решение: В объединение должны войти точки, принадлежащие либо 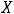 , либо
, либо
. Тогда |
. Точка |
принадлежит |
искомому множеству, |
поскольку она является точкой множества |
. Точка |
принадлежит этому |
|
множеству, так как она принадлежит 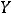 . Ответ: интервал (1,12).
. Ответ: интервал (1,12).
22

Пример 6. Найти объединение множеств: 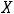

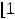
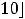 и
и 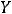

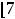
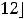 .
.
Решение. Оба множества являются отрезками. Согласно определению объединения множеств имеем 
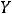

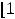
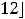 .
.
Ответ: Отрезок [1,12].
Пример 7. Указать |
объединение множеств: |
|
|
|
|
и |
|||
|
|
|
|||||||
|
числового луча |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Очевидно, |
что |
|
|
Таким образом, объединение |
|||||
|
|||||||||
таких лучей (полупрямых) есть вся координатная прямая (числовая ось) 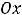 .
.
Ответ:
Пример 8. Найти пересечение конечных множеств 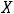


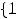
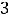
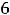
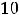
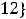 .
.
Решение. Согласно определению пересечения двух множеств (см. задание 2
текстовых заданий с |
решениями) таким множеством будет множество |
||
. Действительно, это множество состоит из общих элементов |
|||
исходных множеств |
, т.е. из элементов, принадлежащих как |
так и . |
|
Ответ: пересечением заданных множеств является множество {3,6,10}. |
|||
Пример 9. Найти пересечение множеств |
и |
. |
|
Решение. Общим элементом исходных множеств является только один
элемент |
. Следовательно, |
={5}. |
|
||||||||
Ответ: {5}. |
|
|
|
|
|
||||||
Пример |
10. |
Указать пересечения следующих конечных |
множеств: |
||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Так |
как заданные |
множества не имеют общих |
элементов, то |
|||||||
|
|
|
|
, т.е. пересечением является пустое множество. |
|
||||||
Ответ: |
|
пустое множество. |
|
|
|||||||
|
|
|
|||||||||
Пример 11. Найти объединение и пересечение следующих бесконечных
множеств: множества нечётных чисел |
|
|
и множества |
|
|
||||
чётных чисел |
. |
|
|
|
Решение. |
Очевидно, что |
т.е. объединением |
||
является множество N натуральных чисел. Так как общих элементов множества |
||||
не имеют, то пересечением является пустое множество. |
|
|||
Ответ: |
. |
|
|
|
Пример12. Найти пересечение следующих пар множеств: |
|
|||
1) |
; |
|
|
|
|
23 |
|
|
|

2) 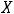
 3)
3) 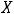
 4)
4) 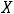
 5)
5) 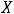

6) 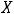

Решение. Все множества являются промежутками. При этом в первых двух
случаях оба |
множества |
являются отрезками. В первом случае |
есть |
|
подмножество |
( |
, причём |
. Тогда очевидно, что пересечением |
|
является отрезок [3,6]. Во втором случае |
(отметим, что концы |
|||
этого отрезка |
|
принадлежат обоим исходным множеством). |
|
|
В третьем случае данные множества являются интервалами, причём их общей
частью будет интервал (5,10). Точки |
не входят в пересечение, так |
|
как |
не принадлежит |
. |
Вчетвёртой ситуации имеем, что 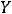
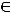
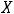 , при этом
, при этом 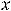

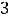 принадлежит обоим исходным промежутком. Тогда пересечением является полуотрезок (1,3].
принадлежит обоим исходным промежутком. Тогда пересечением является полуотрезок (1,3].
Впятом и шестом случаях множества являются числовыми лучами (полупрямыми). В случае 5) имеется только одна общая точка – нуль, тогда
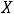
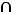
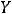

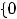
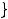 . В ситуации 6) общей точки нет и, следовательно, пересечение есть
. В ситуации 6) общей точки нет и, следовательно, пересечение есть
пустое множество ( |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Ответы: 1)[3,6]; 2)[10,12]; 3) (5,10); 4) (1,3]; 5){0}; 6) |
|
|
пустое множество. |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Пример 13. Имеются следующие уравнения и неравенства: 1) |
2) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3) |
|
|
|
|
|
4) |
5) |
|
|
|
|
|
6) |
|
|
|
|
|
|
|
7) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
8) |
|
|
|
|
|
|
|
Из множества их решений выделить ограниченные и |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
неограниченные множества. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Решение. |
|
|
Множеством |
решений |
уравнения |
|
является |
множество |
||||||||||||||||||||||||||
|
|
|
|
|
|
, уравнения |
|
|
|
|
|
|
|
множество |
|
|
, а уравнения |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
множество |
|
|
|
|
|
. Все эти множества конечны и являются ограниченными. |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
Множеством |
|
|
решений |
неравенства |
|
|
|
|
|
является |
отрезок |
|
|
|
|
; это |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
множество ограничено. Множество решений неравенства |
|
|
|
есть |
|||||||||||||||||||||||||||||||||||
множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
, являющееся |
неограниченным множеством. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Решения неравенства |
|
|
|
|
|
|
|
принадлежат |
|
отрезку |
|
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
являющемуся ограниченным множеством. Множеством решений неравенства
|
|
является множество |
|
|
|
, являющееся |
|
|
|
|
|||
неограниченным. Последнее неравенство |
|
|
|
выполняется для любых |
||
24 |
|
|
|
|
||
действительных чисел, т.е. множеством его решений является неограниченное множество 

Ответы: ограниченными являются множества решений уравнений 1), 2), 5) и неравенств 3), 6); неограниченными являются множества решений неравенств 4), 7) и 8).
Пример 14. Указать множество, на которое отображает отрезок – 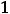
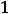 функция
функция 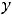

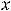 .
.
Решение. Проще всего дать ответ, построив график этой функции, который
имеет вид |
|
||
|
|
|
1 |
-1 |
1 |
||
Рисунок 1 – График функции |
|||
Из рисунка 1 видно, что отрезок |
|
|
отображается на отрезок |
|
|||
Ответ: отображением является отрезок |
. |
||
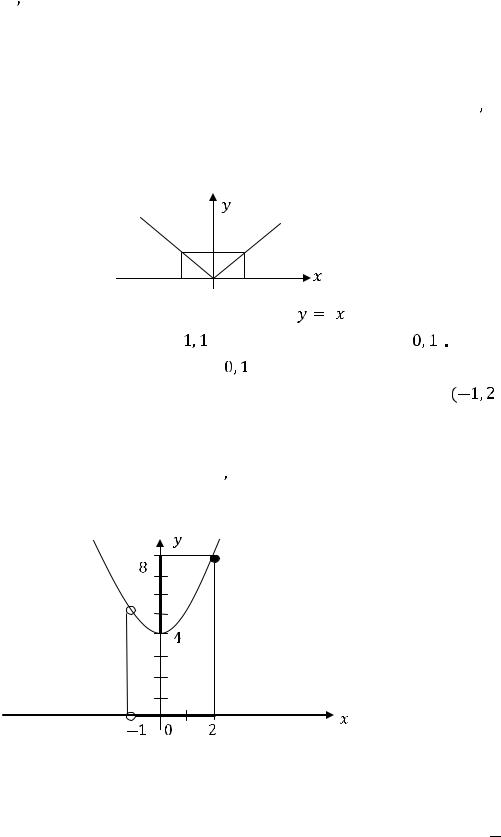
Пример 15. Найти множество, на которое отображает полуотрезок функция 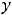

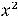
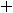
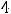

Решение. Обычно есть желание вычислить значения этой функции на концах исходного полуотрезка (в точках 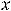


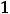
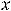

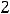 ) и исходя из этого сделать вывод. Так поступать нельзя, поскольку функция на этом полуотрезке не является строго монотонной. Построим график функции:
) и исходя из этого сделать вывод. Так поступать нельзя, поскольку функция на этом полуотрезке не является строго монотонной. Построим график функции:
Рисунок 2 – График функции 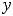

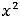
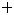
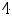
Из рисунка 2 видно, что отображением является множество [4,8]. Этот отрезок отмечен на оси 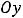 (исходный полуотрезок (-1,2] отмечен на оси
(исходный полуотрезок (-1,2] отмечен на оси 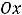 ). Действуя так, как сказано ранее, получили бы неправильный ответ полуотрезок (5,8].
). Действуя так, как сказано ранее, получили бы неправильный ответ полуотрезок (5,8].
25

Ответ: отображением является отрезок [4,8]. |
|
Пример 16. Выяснить отображение интервала (0,64) функцией |
. |
Решение. Функция определена на луче (0,+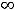 ) и является на этом множестве строго возрастающей, причём областью значений (отображение этого луча
) и является на этом множестве строго возрастающей, причём областью значений (отображение этого луча
функцией) является множество (- |
). Вычислим значение этой функции на |
||
концах заданного |
|
интервала: |
; кроме того, символически можно |
записать |
|
. Так как исходное множество (0,64) открытое (концы не |
|
|
|||
включены), то отображением будет множество (- |
. Построение графика не |
||||||
понадобилось, но рекомендуем читателю это сделать. |
|
|
|
|
|
||
Ответ: отображением является множество (- |
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||
Пример 17. Найти естественную область определения функции |
|
. |
|||||
|
|||||||
Решение. Так как квадратный корень можно извлекать только из
неотрицательных чисел, то должно |
выполняться неравенство |
|
|
|
или |
|||||||||||
|
||||||||||||||||
. |
Множеством |
решений каждого неравенства |
|
является |
множество |
|||||||||||
(- |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: областью |
определения |
функции является |
множество |
(- |
|
|
||||||||||
|
|
|||||||||||||||
|
|
, т.е. объединение лучей (- |
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 18. Указать область определения функции |
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||
Решение. Должно выполняться строгое неравенство 4- |
|
|
|
|
|
, так как на нуль |
||||||||||
делить нельзя. Множеством решений этого неравенства является интервал (-2,2). Ответ: интервал (-2,2).
Пример 19. Найти какую-нибудь функцию, отображающую отрезок [-1,1] на
отрезок [- |
]. |
|
|
|
|
|
|
Решение. |
Такой функцией может быть линейная |
функция |
, |
||||
графиком которой является прямая линия, проходящая через точки (-1, |
) и (1, ). |
||||||
Параметры |
искомой функции найдутся из условия |
прохождения прямой |
|||||
через эти точки. Указанное требование приводит к системе уравнений |
|
||||||
|
|
|
|
|
|
|
|
C неизвестными |
сложив равенства, получим |
т.е. |
; тогда |
|||
. Итак, имеем |
, |
. Следовательно, искомая функция |
. |
|||
Ответ: отображением отрезка [-1,1] |
на отрезок [- |
] является функция |
||||
. |
|
|
|
|
|
|
Пример 20. |
Издержки |
при |
производстве |
некоторой |
продукции |
|
линейно зависят |
от |
объёма |
(ед.) производства. Известно, что при |
|||
|
|
|
26 |
|
|
|

издержки составили 10 у.е. (

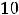 ), а при
), а при 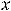

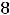

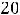
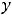

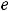

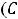

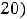 . Найти функцию издержек производства.
. Найти функцию издержек производства.
Решение. По условию сказано, что функция имеет вид 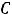

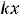
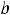 . Параметры найдутся из условия, что график функции проходит через точки (2,10) и (8,20). Это приводит к решению системы уравнений
. Параметры найдутся из условия, что график функции проходит через точки (2,10) и (8,20). Это приводит к решению системы уравнений
Решение этой системы такого: 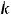

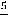
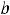

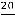 . Таким образом функция имеет вид
. Таким образом функция имеет вид 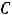

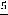
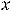
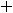
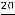 .
.
Ответ: 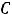

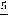
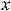
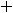
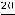 .
.
Пример 21. Выписать первые шесть членов последовательностей, общие члены 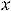 которых заданы следующими аналитическими формулами: 1)
которых заданы следующими аналитическими формулами: 1)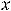

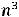
2)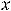

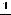 , 3)
, 3)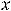


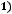 .
.
Решение. Последовательность есть функция 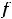 натурального аргумента
натурального аргумента 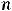 . Областью определения любой последовательности является множество
. Областью определения любой последовательности является множество
натуральных чисел |
. При |
каждом натуральном |
число |
|||
|
есть значение этой функции. Выбирая по порядку расположения |
|||||
числа из |
, будем получать члены конкретной последовательности. |
|
||||
Для |
имеем |
, |
|
|
|
|
|
|
Следовательно, первые шесть членов таковы: 1, 8, |
||||
27, 64, 125, 216. |
|
|
|
|
|
|
Обратимся ко второй последовательности |
|
|
. Напомним, что число |
|||
|
|
|||||
(факториал натурального числа 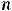 ) есть произведение всех натуральных чисел от 1 до
) есть произведение всех натуральных чисел от 1 до 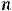 включительно, т.е.
включительно, т.е. 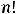

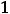

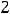

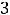



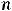
 Так как
Так как 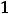


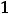
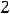


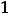

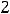

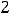
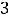


то
Тогда первыми шестью членами этой последовательности
являются числа 1, 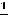
Числитель третьей последовательности имеет вид 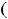

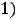
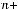
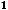 . Он представляет собой последовательность, первые шесть членов которой таковы: 1, -1, 1, -1, 1,
. Он представляет собой последовательность, первые шесть членов которой таковы: 1, -1, 1, -1, 1,
-1. Для самой последовательности 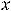


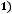 первыми шестью членами будут,
первыми шестью членами будут,
очевидно, числа 1, 
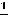 ,
, 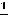 ,
, 
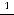 ,
, 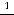 ,
, 
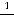 .
.
27

Ответ: 1) 1, 8, 27, 64, 125, 216; 2) 1, 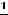
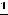
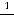
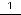
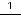 ; 3) 1,
; 3) 1, 
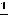 ,
, 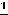 ,
, 
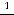 ,
, 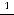 ,
, 
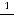

Пример 22. Требуется записать в каком-нибудь виде формулу общего члена каждой из следующих последовательностей:
1)2,4,6, 16, 32, …;
2)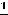
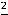
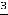
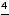
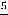 , …;
, …;
3)-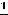
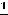

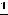
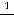

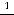 , … .
, … .
Решение. Очевидно, что из формулы |
получаются выписанные члены |
|||
первой последовательности. Эта формула издаёт её |
общий |
член |
, если |
|
предполагать, что закономерность последующих членов |
( |
сохраняется. |
||
Числители второй последовательности пробегают номера n множества N, а каждый знаменатель на единицу больше числителя. Тогда 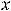

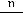 .
.
У третьей последовательности знаки чередуются. Если знаки относить к
числителям дробей, то числа числителей будут получаться из выражения |
|
|
. |
||||||||||||||||||
|
|||||||||||||||||||||
Знаменатели этих дробей получаются из выражения |
(см. первую |
||||||||||||||||||||
последовательность). Таким образом, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: 1) |
; 2) |
|
|
; 3) |
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 23. |
Последовательность |
задана рекуррентным |
соотношением |
||||||||||||||||||
|
|
|
при заданном первом члене |
Найти четвёртый член |
|
||||||||||||||||
этой последовательности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Подставив в рекуррентное соотношение |
, получим |
|
|
|
|
||||||||||||||||
. Так как по условию примера |
, |
|
то |
|
Положим в |
||||||||||||||||
рекуррентном равенстве |
; тогда получим, что |
|
|
Взяв в |
|||||||||||||||||
рекуррентной формуле |
, |
|
получим |
|
|
|
|
требуемый четвёртый |
член |
: |
|||||||||||
|
|
|
|
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 24. Выписать последовательность, у которой |
|
и при |
|||||||||||||||||||
выполняется равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Положим в рекуррентном равенстве |
. Тогда |
|
, и так |
||||||||||||||||||
как по условию |
, |
|
то |
|
|
|
Возьмём теперь |
, |
тогда |
|
|||||||||||
|
|
|
|
|
При |
|
|
имеем |
|
|
|
|
|
|
|
|
. |
При |
|
||
имеем |
|
|
|
|
. И так |
|
далее. |
Окончательно |
получаем |
||||||||||||
следующую последовательность: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,  (каждый её член,
(каждый её член,
28
начиная с третьего, равен сумме двух предыдущих членов, что и дано в рекуррентном соотношении).
Ответ: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,  .
.
Пример 25. Выяснить, какие из приведённых ниже функций чётны, какие
нечётны, а какие не являются ни чётными, ни нечётными: 1) |
|
|
, 2) |
|
, |
||||||||||
3) |
|
|
, 4) |
|
, |
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Функция |
|
, заданная |
на симметричном относительно |
|
нуля |
||||||||||
промежутке, |
называется |
чётной, если |
|
для любого |
аргумента |
|
|
из |
этого |
||||||
промежутка |
выполняется равенство |
|
, и |
нечётной, |
если |
|
|
|
|||||||
|
|
|
|
||||||||||||

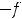
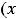
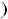 . Если ни одно из этих равенств не выполнено, то функция не является ни чётной, ни нечётной (будет функций общего вида). К таким относится большинство функций.
. Если ни одно из этих равенств не выполнено, то функция не является ни чётной, ни нечётной (будет функций общего вида). К таким относится большинство функций.
График чётной функции симметричен относительно оси ординат, а нечётной – относительно начала координат. График функции общего вида такими симметриями не обладает. По графику можно судить о принадлежности функции к соответствующему классу.
Пусть каждая из функций |
, |
– чётная или нечётная. Тогда легко |
|||
вывести правила (утверждения) |
о чётности или нечётности их суммы |
+ |
|||
, произведения |
и |
частного |
|
. Например, очевидно |
|
|
|||||
утверждение: произведение двух чётных или двух нечётных функций есть функция чётная; произведение чётной функции на нечётную есть функция нечётная.
Функция 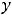

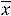 определена на луче
определена на луче 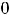
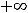
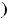 , т.е. на несимметричном относительно начала координат промежутке. Она является функцией общего вида, т.е. не является ни чётной, ни нечётной.
, т.е. на несимметричном относительно начала координат промежутке. Она является функцией общего вида, т.е. не является ни чётной, ни нечётной.
Функция |
|
|
|
определена на всей координатной прямой |
, т.е. на |
|||||
множестве |
|
|
|
, которое симметрично относительно нуля. На основании |
||||||
|
|
|||||||||
свойства |
|
|
|
абсолютной величины числа имеем |
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
, что означает чётность этой функции. |
||||
|
|
|
|
|
|
|||||
Все остальные функции этого примера также определены на всей числовой оси. Для третьей функции имеем равенство 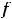

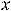


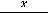


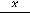

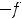
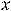
которое означает её нечётность; для четвёртой 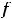

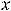

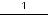

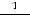

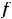
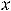 что означает её чётность. Для пятой функции имеем, что
что означает её чётность. Для пятой функции имеем, что 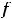

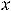

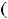

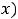
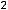
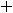
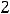
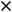
29
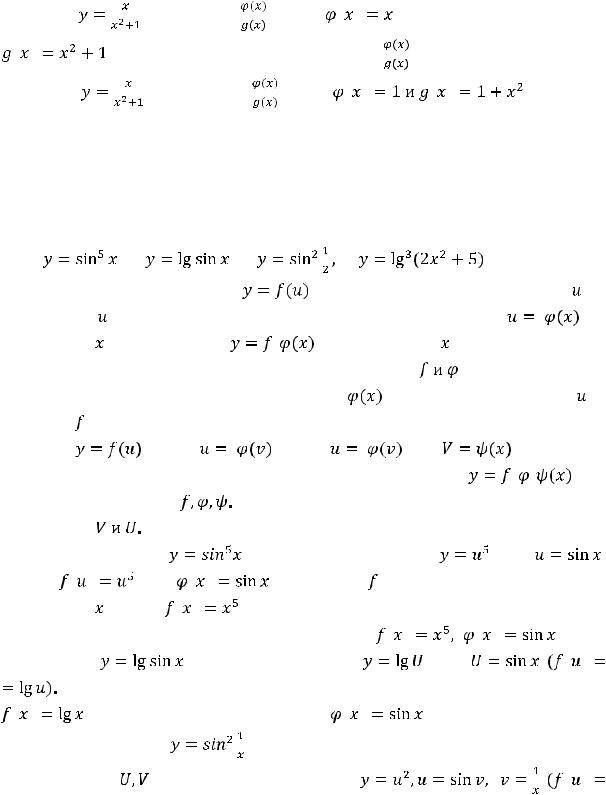
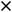

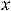
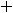
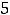

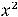

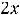
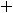
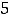 , что не равно ни
, что не равно ни 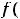
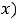 , ни
, ни 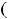
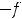
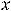
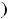 ; функция не относится ни к чётным, ни к нечётным.
; функция не относится ни к чётным, ни к нечётным.
Рекомендуем читателю построить графики всех функций примера.
Для третьей и четвёртой функций можно провести другие рассуждения.
Функция |
|
|
|
|
имеет |
вид |
|
|
, где |
|
есть нечётная функция, а |
||
|
|
|
|
|
|
||||||||
|
|
|
чётная. Очевидно, что |
частное |
|
есть нечётная функция. |
|||||||
|
|
|
|
||||||||||
Функция |
|
|
|
|
имеет |
вид |
|
|
|
, где |
|
являются |
|
|
|
|
|
|
|
|
|
||||||
чётными функциями. Тогда, очевидно, частное будет чётной функцией. Ответы: первая и пятая функции примера являются функциями общего вида,
вторая и четвёртая – чётными, третья – нечётной.
Пример 26. Указать функции, композициями (суперпозициями) которых
являются следующие сложные функции: |
|
|
|
|
|
|
|
|
|
|
|||||||||
1) |
, 2) |
, 3) |
|
|
|
4) |
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. |
Пусть |
функция |
|
|
|
|
есть |
функция |
от переменной |
, а |
|||||||||
переменная |
(промежуточная |
|
переменная) является |
функцией |
|
|
|
от |
|||||||||||
переменной |
. Тогда функция |
|
|
|
|
от переменной |
называется сложной |
||||||||||||
функцией (композицией или суперпозицией) функции |
|
. Сложная функция |
|||||||||||||||||
получилась |
путём |
подстановки |
функции |
в качестве |
аргумента |
|
в |
||||||||||||
функцию . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
, |
где |
|
|
, |
где |
|
и |
|
|
, то путём |
||||||||
соответствующих подстановок получим сложную функцию |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
композицию функций |
При этом использовались две |
промежуточные |
|||||||||||||||||
переменные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первую функцию |
|
|
|
можно записать в виде |
|
, |
где |
. |
|||||||||||
Тогда |
, а |
|
|
|
|
; |
функция |
как |
функция |
независимой |
|||||||||
переменной |
такова: |
|
|
, т. е. является степенной функцией. Итак, первая |
|||||||||||||||
сложная функция является композицией функции |
|
|
|
. |
|
|
|
||||||||||||
Функция |
|
записывается в виде |
|
, |
где |
|
|
|
|
|
|
|
|||||||
Итак, эта сложная функция есть композиция логарифмической функции |
|||||||||||||||||||
и тригонометрической функции |
|
. |
|
|
|
|
|
|
|
|
|||||||||
Третья функция |
|
|
|
записывается |
с помощью |
промежуточных |
|||||||||||||
|
|
|
|||||||||||||||||
переменных |
|
следующим |
|
образом: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
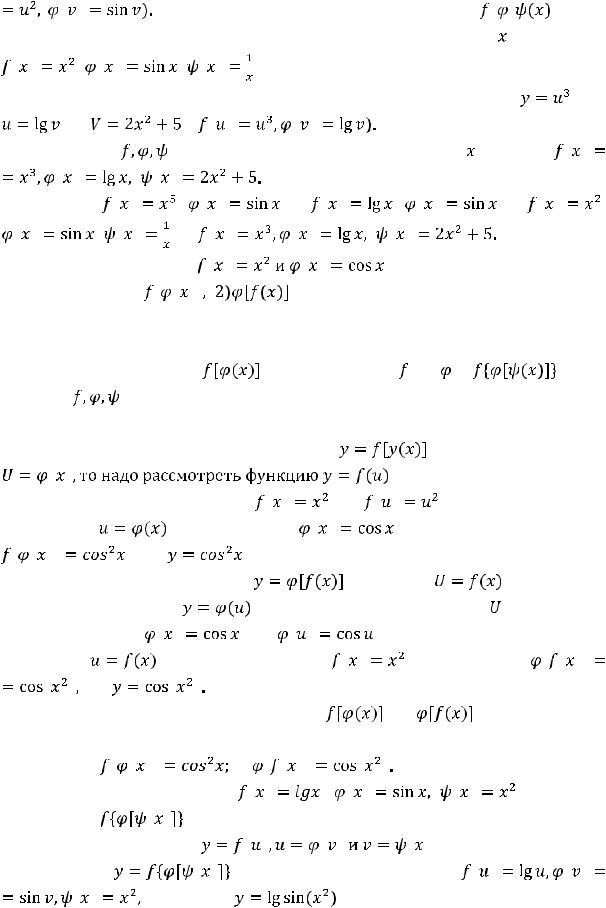
|
Таким образом, функция имеет вид |
|
|
, т.е. |
|||||
является композицией трёх функций. |
Как функции переменной |
они таковы: |
|||||||
, |
, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обратимся к последней функции, |
которая записывается в виде |
, где |
|||||||
и |
( |
|
|
|
Снова имеем |
суперпозицию |
|||
трёх функций |
, которые |
|
как |
функции |
переменной |
таковы: |
|
||
Ответ: 1) |
, |
; |
2) |
, |
|
; 3) |
, |
||
, |
|
; 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 27. Из функций |
|
|
|
составить следующие композиции |
|||||
(сложные функции): 1) |
|
|
|
|
. |
|
|
|
|
Решение. В предыдущем примере при заданной функции выявлялись функции, образующие данную композицию. При этом рассматривались
следующие |
композиции: |
|
(двух функций |
и |
), |
(трёх |
|
функций |
). В этом примере для двух функций решается обратная задача, |
||||||
причём будет показано, что важен порядок образования композиций. |
|
||||||
Получим |
первую |
композицию |
|
. |
Если |
положить |
|
|
|
|
|
|
промежуточной переменной |
||
U. Так как по условию примера |
|
, то |
|
. В эту формулу надо |
|||
подставить |
(по |
условию |
|
). В |
результате получим |
||
|
, т. е. |
. |
|
|
|
|
|
Для получения композиции |
|
положим |
. |
Тогда надо |
|||
рассмотреть |
функцию |
|
промежуточной |
переменной . Так как по |
|||
условию примера |
, |
то |
. В последнее равенство надо |
||||
подставить |
(по условию примера |
|
). Получим, что |
||||
т.е. |
|
|
|
|
|
|
|
Обратим внимание, что композиции |
|
и |
есть |
различные |
|||
функции. |
|
|
|
|
|
|
|
Ответ: 1) |
|
2) |
|
|
|
|
|
Пример 28. Из функций |
, |
|
|
|
образовать |
||
композицию |
. |
|
|
|
|
|
|
Решение. |
Если взять |
|
|
|
, |
то получим нужную |
|
композицию |
|
. |
Так как |
по условию |
|
||
|
то получим |
|
. |
|
|
|
|
|
|
|
31 |
|
|
|
|

Ответ: 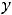

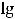
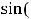
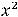
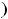 .
.
Пример 29. Найти обратные функции к следующим функциям: 1)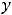

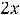
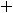
Решение. Сначала приведем понятие обратной функции и укажем условие её
существования. |
|
|
Пусть |
– действительные переменные, а |
являются |
соответствующими множествами их изменения. Обычно любым из этих множеств является некоторый промежуток. Промежуток может быть любого
типа, |
например отрезок. |
Интервал, |
какой-нибудь полуотрезок или луч, |
||||||
( |
|
|
|
|
всё множество вещественных чисел. |
|
|
||
|
|
|
|
|
|||||
|
|
Пусть каждому числу |
по некоторому правилу (закону) |
поставлено в |
|||||
соответствие единственное число |
. Тогда говорят, что имеется однозначная |
||||||||
функция |
. Если множество |
есть некоторый промежуток, |
|||||||
то |
называют областью определения функции |
и записывают |
. Если образ |
||||||
множества |
|
|
совпадает с |
|
|
|
|
|
|
называют |
|||||||||||
множеством значений этой функции. При этом переменная |
называется |
||||||||||||||||||||
независимой (аргументом функции |
|
, а |
|
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||||||||||
Если при описанном соответствии каждому |
|
|
можно по |
некоторому |
|||||||||||||||||
правилу (закону) |
|
поставить в соответствие единственное число |
, |
то |
|||||||||||||||||
говорят, что имеется обратная к |
|
функция |
|
|
|
|
|
. |
Для |
неё |
|||||||||||
применяют ещё обозначение |
|
|
|
|
|
|
|
|
|
|
. При этом говорят, |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
что исходная функция обратима. Переменная |
является аргументом функции |
||||||||||||||||||||
, числа |
являются значениями этой функции. Множество |
является её |
|||||||||||||||||||
областью определения, а множество |
|
|
|
областью значений. |
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
Если |
|
|
является обратной для |
|
то функция |
|
будет |
||||||||||||||
|
|
|
|||||||||||||||||||
обратной для |
|
|
поэтому |
функции |
|
|
|
|
|
|
называют |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
взаимно обратными. При этом будут выполняться следующие соотношения:

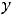 .
.
Справедливо утверждение: всякая строго монотонная функция (строго убывающая или возрастающая ) имеют обратную.
Условие строгой монотонности является достаточным ( но не необходимым) для существования обратной функции. Обратную функцию могут иметь и нестрого монотонные функции. Однако в утверждении слова «строго монотонная». Легко указать примеры, когда неубывающая (невозрастающая) функция обратной не имеет.
32
Справедлива ещё следующая теорема: если определённая на промежутке 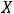 с
с
областью значений на промежутке |
функция |
строго монотонна и |
||
непрерывна, то обратная функция |
на промежутке |
также непрерывна |
||
и имеют ту же строгую монотонность. |
|
|
|
|
Графики функций |
и |
в системе координат |
совпадают. |
|
Но так как принять аргумент любой функции обозначать через 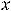 , а её значение –
, а её значение –
через |
то обратную |
функцию надо |
|
записать |
в виде |
|
|
|
|
||||||||||||||||||||
|
|
|
Тогда график обратной функции симметрично отразится относительно |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
прямой |
– биссектрисы первого и третьего координатных углов. |
|
|
|
|
||||||||||||||||||||||||
Если функция |
|
|
задана аналитическим выражением |
|
, то для |
||||||||||||||||||||||||
получения аналитического выражения обратной функции |
надо решить |
||||||||||||||||||||||||||||
уравнение |
|
|
относительно |
. Такое выражение |
через |
не |
всегда |
||||||||||||||||||||||
существует (не выражается через элементарные функции). |
|
|
|
|
|||||||||||||||||||||||||
Обе рассматриваемые в примере |
функции определены, непрерывны и строго |
||||||||||||||||||||||||||||
возрастают на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для нахождения обратной функции |
|
к функции |
разрешим это |
||||||||||||||||||||||||||
уравнение |
относительно |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
(эта |
функция и |
является |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
обратной). Её надо записать в виде |
|
|
|
|
|
|
|
. Ясно, что областью определения |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
является |
множество |
|
|
. |
На |
|
нём |
функция |
непрерывна |
и |
строго |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
возрастает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Разрешив уравнение |
|
относительно |
, |
получим |
(обратная |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
функция). Сменив обозначения переменных на общепринятые, получим |
. |
||||||||||||||||||||||||||||
Функция определена |
на всей числовой оси, |
|
при этом непрерывна и строго |
||||||||||||||||||||||||||
возрастает.
Графическое изображение исходных и обратных им функций дано на рисунках 3, 4.
33
