Сапунов Прогнозирование ползучести и длителноы прочности 2015

ния. Например, для представительной диаграммы длительной прочности можно выделить до пяти характерных участков, требующих поэтапного описания.

Очевидно, что «поэтапная» аппроксимация экспериментальных данных приводит к неоправданному увеличению числа параметров, что существенно усложняет их определение на имеющейся базе данных и делает последующую процедуру прогнозирования более неустойчивой и поэтому менее надежной. При сокращении участков по тем или иным причинам теряется экспериментальная - ин формация в переходных зонах между выделенными участками.

Единая кривая дает возможность экстраполировать имеющиеся экспериментальные данные в сторону больших значений нужного параметра за счет аналогичных опытов, проведенных при других, измененных составляющих скел-фактора (вектора условий проведения опыта), например при повышенной температуре и т.п. Другими словами, гипотеза единой кривой является основой статистического многовариантного прогнозирования рассматриваемого процесса деформирования или разрушения.

Соотношения (4.4) и (4.5) в логарифмических координатах описывают «параллельный перенос» изотерм долговечности (в общем случае - кривых деформирования или разрушения одного семейства) и позволяют сделать вывод о логарифмической совмещаемости рассматриваемых кривых.

Методика совмещения (или параллельного переноса) первичных кривых деформирования или разрушения в логарифмических координатах весьма просто и наглядно демонстрируется с помощью листа прозрачной бумаги (кальки) как поступательно перемещаемого транспаранта, на котором следует изобразить одну из кривых.

Данная процедура распознавания кривых, конгруэнтных в логарифмических координатах, легко алгоритмизируется, уточняется и реализуется при заданном уровне доверия. В качестве критерия адекватности и распознавания кривых оправдано применение среднеквадратичного критерия Гаусса в логарифмических координатах, что обусловлено логарифмически нормальными законами распределения величин y при фиксированных x и наоборот. Это

позволяет использовать хорошо разработанный аппарат дисперсионного анализа, исходя из требуемого уровня доверительной веро-

82

ятности и рассматривая в качестве аргумента в формуле типа(4.4) либо x , либо y . Поскольку «остаточная дисперсия» временных

рядов, определяемая лишь из повторных экспериментов, является, как правило, неизвестной, возможна более щадящая процедура распознавания кривых на основании критерия Фишера.

Отметим, что предложенный алгоритм распознавания аффинноподобных кривых носит параметрический характер: экспериментальные точки предварительно сглаживаются некоторыми аналитическими зависимостями либо формально, либо с позиций содержательного анализа, отдающего предпочтение моделям определенного класса. Очевидно, что любая параметрическая процедура порождает новые погрешности, оцениваемые соответствующей дисперсией. Непараметрический подход, к тому же свободный от дополнительной операции логарифмирования, еще ждет своей разработки.

Приведем пример, подтверждающий справедливость вывода о логарифмической совмещаемости кривых деформирования или разрушения и возможность построения единой кривой.

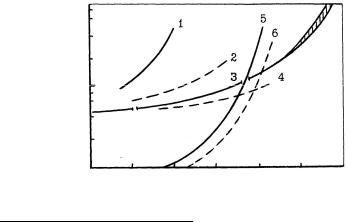
На рис. 4.1 показаны уникальные кривые ползучести для жаропрочной стали1 (кривые 1, 2 соответствуют значениям s и T , рав-

ным 647 МПа и 500o C ; 3, 4 – 585 МПа и 500 oC ; 5, 6 – 77 МПа и

700 oC ; сплошная линия – растяжение, пунктирная – сжатие).

e, %

4,0

2,0

1,0

0,4

0,2

0,1

1 Tilly F.P., Harrison F. Relation ships for tensile creep under transient stresses. J. of strain analysis. 1972. V. 7. № 1. P. 61 – 68.

83

С помощью кальки легко убедиться в совмещаемости кривых ползучести.

На кривой 3 рис. 4.1 показана единая кривая, построенная на 20 первичных точечных совокупностях(здесь показана обработка только лишь 6 совокупностей) при трех составляющих скел-факто- ра x = {s, T , Ls }: напряжения s , температуры T и параметра Ло-

де Ls , определяющем тип напряженного состояния( Ls = -1 - растяжение, Ls =1 - сжатие). Единая кривая экстраполирует

опытные данные почти на два десятичных порядка. Заштрихованная область определяет зону разброса экспериментальных точек.

4.4.Единая кривая и «эталонные качества процесса»

иих применения

Гипотеза единой кривой позволяет достаточно просто с помощью процедуры статистического распознавания«логарифмически параллельных» (совмещаемых) кривых одного семейства решать следующие практически важные задачи:

или более простой процедуры дискриминации моделей на основании критерия Фишера.

84

4.4.1. Статистическое прогнозирование процесса деформирования или разрушения

Построение единой кривой на базе экспериментальных данных,

анализируемого процесса деформирования или разрушения.

Можно утверждать, что составляющие скел-фактора являются равноправными в том смысле, что каждый из них смещает графический образ кривой деформирования(или разрушения), не меняя ее формы, что, в свою очередь, говорит о физическом подобии процессов при различных значениях этих составляющих. Так, на рис. 4.1 на кривой 3 показана единая кривая, построенная при разных значениях трех составляющих скел-фактораx = {s, T , Ls }. Данное обстоятельство позволяет утверждать, что для рассматриваемого материала существуют такие зоны изменения скел-фактора

ˆ некоторое предельное значение вектора условия проведения x -

опыта x = const . Компонентами этого вектора, как уже отмечалось, могут быть температура, тип напряженного состояния, скорость нагружения, интегральный поток облучения и т.п.

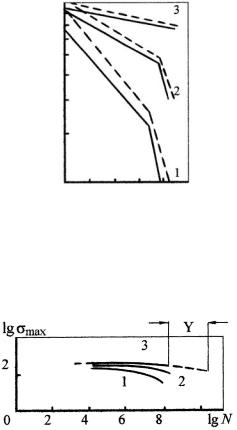
В качестве еще одного примера рассмотрим экспериментальные кривые усталостной прочности никелевого сплава для разных частот при повышенных температурах. Соответствующие изотермы выносливости, построенные при двух составляющих скел-фактора x = {T , w }( T - температура; w - частота) приведены на рис. 4.2

(кривые 1 – 3 - T равно 900, 800, 700 °С; сплошные и пунктирные линии - w равно 50 и 200 Гц ).

85

s-1 , МПа

300

200

150

100

50

Рис. 4.2

Эти же опытные данные для w = 50 Гц показаны на рис. 4.3 в логарифмической сетке с модулем, равным для обеих осей (кривые 1 – 3 – то же, что и на рис. 4.2).

Рис. 4.3

В справедливости утверждения о логарифмической совмещаемости приведенных кривых усталости легко убедиться, наложив на рис. 4.3 кальку и начертив на ней одну из кривых. При параллельном переносе кальки-транспаранта можно добиться оптимального совпадения начертанной кривой с любой другой на исследуемом рисунке. Здесь же с использованием параллельного переноса нижних кривых к верхней изотерме усталостной прочности, отвечающей температуре T = 700 °С, пунктиром построена единая кривая. Упреждение Y по оси lg N составляет 2,6 десятичных порядка.

86

Иными словами, предложенная процедура температурновременного прогнозирования позволяет уменьшить продолжительность эксперимента при T = 700 °С в 780 раз за счет осуществления аналогичных опытов при повышенной на 200 °С температуре.

Учитывая традиционный для циклического разрушения разброс экспериментальных данных правомерность утверждения о логарифмической совмещаемости кривых выносливости можно проверить на требуемом уровне риска(обычно p = 5 %). Очевидно, что эта задача решается корректно лишь в том случае, если оценивается разброс экспериментальных точек при параллельных циклических испытаниях нескольких образцов-близнецов. Апостериори, опираясь на кривые статической усталости, можно принять дисперсию величины lg N равной 0,10 ¸ 0,17 .

4.4.2.Спецификация математических моделей описания процесса деформирования или разрушения

Соотношения (4.4) и (4.5) являются вполне удовлетворительным математическим доказательством утверждения, что изменение внешних факторов (параметров эксперимента) не меняет идентификатор функции j , описывающей рассматриваемый процесс де-

формирования или разрушения, а меняет лишь ее масштабные параметры по обеим координатным осям. Другими словами, принцип

ность: каждая кривая моделирует любую другую и общим для них является “изофункционализм” или “качество” процесса.

Поскольку все кривые одного семейства для рассматриваемого материала описываются независимо от условий эксперимента одним и тем же функциональным идентификаторомj , «качество процесса» можно выделить в «чистом виде». Для этого достаточно конкретизировать в соотношении типа(4.1) масштабные коэффициенты, полагая их равными единице(для длительной прочности, например y* = t* =1ч, x* = s* =1МПа) и, тем самым, выделяя “в чистом виде” эталон формы (эталон «качества процесса») соотно-

87

шения (4.1). Форма построенного эталона «качества процесса» зависит только от выбранной функции j .

Принцип использования эталонных кривых в графической интерпретации заключается в совмещении соответствующих шаблонов, построенных на кальке, с исследуемыми экспериментальными кривыми (или точечными совокупностями) деформирования или разрушения одного семейства и в выявлении их конгруэнтности или отсутствия таковой. Добавим, что шаблоны строятся в логарифмических координатах с тем же логарифмическим модулем, что и экспериментальные данные.

Представленная процедура пригодна для визуального распознавания математической модели, наиболее адекватной опыту, и позволяет уже в первом приближении, часто достаточном для практических надобностей, судить о возможности применения каждой из рассматриваемых конкурирующих закономерностей для описания рассматриваемого процесса деформирования или разрушения.

Указанный графический процесс сопоставления шаблона и эксперимента легко алгоритмизируется и реализуется на ПК с применением выбранного критерия адекватности. В качестве меры “согласия” удобно взять среднеквадратичный критерий Гаусса, записанный в логарифмических координатах.

Примеры дискриминационного анализа математических моделей описания процесса деформирования или разрушения, связанные с выбором модели(из нескольких конкурирующих), наиболее адекватной эксперименту, будут рассмотрены ниже.

4.4.3. Нелинейная параметризация математических моделей описания процессов

Определение параметров, входящих в математическую модель, принятую для описания тех или иных опытных данных, представляет достаточно сложную задачу математической теории обработки эксперимента - задачу нелинейного регрессионного анализа.

Основные трудности нелинейной параметризации заключаются в следующем:

достаточно сложен выбор начальных приближений, призванный обеспечивать быструю ,ижелательно, монотонную сходимость итерационных процедур;

88

процедура нелинейного оценивания, как правило, весьма неустойчива и неоднозначна из-за слабой обусловленности корреляционных матриц ошибок;

невелика надежность найденных параметров, поскольку их основные ошибки и доверительный расчетный интервал в большинстве случаев не определяются.

Сформулированный в разделе4.1 метод преобразования масштабов, как способ нелинейной параметризации, позволяет весьма наглядно, надежно и на требуемом уровне доверия определять три коэффициента для уравнения вида(4.1): параметр формы для функционального идентификатора j рассматриваемой математической модели или, что то же самое, для эталонной кривой (если

это необходимо) и две характеристики материала y* , x*. Сравнительно простое графическое решение этой задачи можно

построить с использованием шаблонов эталонных кривых(эталонов «качества процесса»), построенных на кальке. Напомним, что «качество процесса» можно выделить в «чистом виде», конкретизируя в соотношении типа (4.1) масштабные коэффициенты, полагая их равными единице. Считаем, что полученный эталон формы («качества») может включать один параметр, давая дискретные значения которому (например, 0, 1, 2, 3 и т.д.), будем иметь несколько эталонных кривых. Соответствующие шаблоны строятся на кальке в логарифмических координатах с тем же логарифмическим модулем, что и экспериментальные данные; начало координат логарифмической сетки шаблона обозначим как 0ш .

Кальку с построенными шаблонами следует накладывать на анализируемые опытные данные, применяя лишь процедуру параллельного переноса, до визуального совпадения одной из эталонных кривых с экспериментальными кривыми. Тем самым указанной процедурой совмещения будет выделена эталонная кривая, наиболее адекватной опыту, и определен параметр эталона формы функционального идентификатора j рассматриваемой математической

модели.

Накладывая далее кальку на опытные данные до оптимального визуального совпадения выделенной эталонной кривой с экспериментальными точками (или экспериментальной кривой), определим

89

коэффициенты y* , x* , как координаты точки 0ш в логарифмической сетке, принятой для экспериментальных данных.

Описанный процесс графоаналитического определения коэффициентов уравнения типа (4.1) легко алгоритмизируется и реализуется с применением того или иного критерия адекватности. Найденные таким образом три коэффициента уравнения типа (4.1)при необходимости уточняются с помощью итерационной процедуры, что дает возможность построить доверительные интервалы для нелинейной регрессии на требуемом уровне риска.

Приведенные в разделе 4.1 математические обоснования принципа аффинного подобия изотерм долговечности, реализованного в форме метода преобразования масштабов, носят достаточно об-

щий характер и позволяют распространить его на другие первичные “изокривые” одного семейства, описывающие анализируемое явление (процесс).

Возможность применения принципа аффинной эквивалентности к любым первичным “изокривым” одного семейства сводится к представлению соответствующих уравнений в аффинно-подобной форме и проверке конгруэнтности соответствующих логарифмических гомологий при переходе к логарифмическим координатам.

Как пример применения принципа аффинной эквивалентности, рассмотрим задачу прогнозирования ползучести слоистых клееных деревянных балок.

Широкое распространение в современной промышленности материалов органического происхождения и полимеров требует знания их поведения под нагрузкой и механических свойств, которые в сильной степени зависят от времени. Поскольку ползучесть таких материалов заметно проявляется уже при нормальных температурах и невысоких (сравнительно с металлами) нагрузках, то наряду с физико-механическими свойствами необходимо получать характеристики, используемые для предсказания долговечности элементов конструкций в эксплуатационных условиях.

Кроме того, характеристики полимеров и материалов органического происхождения малостабильны и существенно зависят от технологии и технологических параметров их изготовления, времени выдержки между получением материала и его испытани-

90