Никитенко Нестационарные процессы переноса и 2011

нения (1.20) появится член, описывающий рекомбинацию электронов и дырок (см. раздел 1.7.4).

Уравнения (1.18)–(1.20) образуют полную систему уравнений для анализа неравновесного монополярного транспорта электронов (или дырок) в малосигнальном режиме. К сожалению, точное аналитическое решение даже в этом простейшем режиме при произвольном распределении g(E) при любых значениях переменных x и t неизвестно. Практически точные (хотя и с некоторыми ограничениями по времени) решения для плотности носителей N(x,t), полученные для определённого распределения ловушек, приведены в разделе 1.4.4.

1.4.3. Приближённые аналитические решения

Будем считать, что носители заряда генерируются в проводящих состояниях, как это обычно бывает при фотоили радиационной генерации, в момент t = 0 . Аналитическое описание энергетической релаксации и транспорта неравновесных носителей заряда значительно упрощается, если разделить все ловушки на группы. Ловушки, освобождением с которых ранее захваченных носителей к моменту t можно (нельзя) пренебречь, в дальнейшем называются глубокими (мелкими), соответственно [1:17, 30-32]. В момент генерации носителей, t = 0 , все ловушки являютcя глубокими. В соответствии с распределением Пуассона вероятность того, что ловушка остаётся глубокой к моменту t , можно определить следующим образом:

Wd (E,t)= exp −ω(E)t ≡ exp{−ν0t exp −(EC − E)kT }. (1.22)

Поскольку зависимость Wd от энергии является очень резкой, при ν0t >>1 и сильном беспорядке вместо формулы (1.22) можно, как

где η(E) – ступенчатая функция, т.е. считать, что глубокими являются все ловушки с энергиями ниже демаркационной энергии Ed (t ), которая определяется условием

41

Из уравнений (1.22) и (1.24) для Ed (t ) получена следующая за-

Понятие демаркационной энергии, которая разделяет мелкие и глубокие (в данный момент) ловушки, очень важное для теоретического анализа неравновесного транспорта в неупорядоченных материалах, было впервые введено Руденко и Архиповым в работе [1:32]. Зависящие от времени плотности глубоких ловушек

gd (E,t ) и мелких ловушек gsh (E,t ) определяются следующим

Если ловушка с энергией E является мелкой, квазиравновесная заселённость уже в основном установилась, и в уравнении (1.18) можно считать, что левая часть равна 0. Если ловушка глубокая, можно пренебречь вторым членом в правой части (1.18), который описывает освобождение носителей. Решив приближённые уравне-

ния с начальным условием ρ(x,0, E) = 0 и выполнив интегрирова-

ние по энергии согласно (1.19), подробнее см. в разделе 3.5.2, получаем уравнение, которое связывает полную плотность и плотность свободных носителей:

Первое слагаемое в квадратных скобках в (1.27) описывает вклад в полную плотность свободных носителей (им можно пренебречь при t >> τ0 ), второе – вклад носителей, занимающих мелкие ловуш-

ки, а последнее слагаемое – плотность носителей, захваченных на

42

глубокие ловушки. Интегрирование уравнения (1.20) по времени даёт

N0 (x,t ), получаем замкнутое уравнение для полной плотности

N (x,t ):

Правая часть (1.31) описывает захват носителей на глубокие ловушки. Уравнение (1.31), как будет показано ниже, даёт достаточно точное описание неравновесного дрейфа носителей заряда. Однако, как будет показано в разделе 3.5.2, точность этого уравнения недостаточна для описания дисперсии носителей заряда при достаточно сильном поле (диффузионный член нуждается в уточнении).

Пренебрегая диффузией, методом характеристик получено [1:17, 30] ограниченное решение уравнения (1.31) с начальным ус-

которое отвечает генерации носителей в начальный момент в виде тонкого слоя при x = 0 с поверхностной плотностью σ0 :

шение (1.34) полезно для анализа данных времяпролётных экспериментов при временах, много меньших времени пролёта (см. раз-

делы 5.1, 5.2).

43

Если энергетическое распределение убывает с ростом глубины ловушки достаточно быстро, так что интеграл (1.28) в пределе t → ∞ сходится, происходит переход к квазиравновесному (нормальному, гауссовскому) режиму переноса (все ловушки можно

считать мелкими). При этом τ(t )→ ∞ , λ(t )→ 0 , θ1 (t )→ θ , где

так что уравнение (1.31) принимает вид обычного уравнения дрейфа – диффузии,

при x = μeq F0t функция (1.37) имеет резкий максимум.

Совершенно иной вид имеет решение уравнения (1.31) на малом (после импульса генерации) интервале времени, а именно: при выполнении условия [1:17, 30]

Поскольку зависимости τ(t ), θ1 (t ) часто можно аппроксими-

ровать степенной функцией, вместо (1.38) можно пользоваться более простым и грубым выражением:

Поделив уравнение (1.31) на λ(t ), можно при данном условии

пренебречь членом, который содержит производную от времени. Получается замечательно простое уравнение

μ0 F0τ(t )∂Ndisp (x,t ) − D0τ(t )∂2 Ndisp (x,t ) + Ndisp (x,t )= Ndisp (x,0),(1.40)

∂x ∂x2

которое содержит время лишь в качестве параметра, через функ-

44

цию τ(t ) . Уравнение (1.40) полученное в работах Архипова и Ру-

денко [1:17, 30], основано на приближении, согласно которому можно пренебречь вкладом мелких ловушек в процесс переноса. Тогда можно пренебречь первым членом в правой части уравнения

(1.27). Подстановка полученного выражения для N0 (x,t ) в (1.30)

приводит к уравнению (1.40). Данное приближение будем называть приближением сильнонеравновесного транспорта (СНТ). Более точный (но математически более сложный) формализм, основанный на уравнении (1.31), будем называть моделью неравновесного транспорта (НТ). Пренебрегая диффузией, получаем решение урав-

нения (1.40):

Решение (1.41) отвечает случаю сильно неравновесного, или дисперсионного транспорта (см. раздел 2.1.3). Решение (1.41) показывает, что отношение среднеквадратичной дисперсии к дрейфовому сдвигу не зависит от времени (более того, в данном приближении обе эти величины равны), в то время как при нормальном транс-

порте disp (t )x(t ) t−12 . В дисперсионном режиме x(t ) = μ0 F0τ(t ), так что дрейфовая скорость убывает со временем.

1.4.4. Точные аналитические решения

В данном разделе приведены аналитические решения системы уравнений модели многократного захвата, не требующие разделения на «мелкие» и «глубокие» ловушки, для случая экспоненциального распределения ЛС по энергии:

В случае (1.42) равенства (1.26), (1.29) и приближение (1.23) дают

α = kTE1 ( E1 – характерная энергия экспоненциального распределения), Γ(x) – гамма-функция.

45

Для распределения (1.42) из системы уравнений (1.17), (1.19) и (1.20) (без диффузии) получено при t >> τ0 [1:33] линейное интегродифференциальное уравнение

[1:34]. Довольно громоздкое решение уравнений (1.43)–(1.44), полученное для начальных условий (1.33) и α =12 [1:33], сущест-

функция τ(t ) даёт правильную зависимость дрейфового сдвига и дисперсии пакета носителей от времени. Интегрируя (1.47), не-

46

трудно получить disp (t )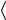x(t ) ≈ 0,76 , что несколько меньше еди-

ницы, которую даёт приближение СНТ, см. уравнение (1.41), но так же не зависит от времени. Результаты расчёта концентрации согласно уравнениям (1.41) и (1.47) показаны на рис. 1.8. Как видно,

решения достаточно хорошо совпадают в области x ≤μ0 F0τ(t ), где сосредоточено большинство носителей. В то же время асимптотические зависимости при x >> μ0 F0τ(t )сильно отличаются. Тем не

менее приближённое решение (1.41) даёт хорошую точность при вычислении переходного тока для условий времяпролётного эксперимента (см. гл. 2) при условии α ≤12 , как это показано в разделе

5.3, потому что функция N (x,t ) усредняется по координате.

многие носители «застревают» на глубоких ловушках. Однако, вследствие «расплывания» пакета со временем его «центр тяже-

сти», т. е. средняя координата носителей 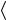x(t ) , всё же растёт со

временем. Рис. 1.8. наглядно показывает, почему сильно неравновесный перенос называют дисперсионным (дисперсия аномально велика и практически равна дрейфовому сдвигу).

Экспоненциальное распределение ловушек (1.42) широко применяется при анализе дисперсионного транспорта в неорганических неупорядоченных полупроводниках [1:5, 13, 17]. Повидимому, его можно также применять для описания радиационной электропроводности в некоторых полимерах [1:13], см. разделы 2.2 и 3.3, хотя для многих материалов наиболее подходящим считается гауссовское распределение ЛС (см. разделы 3.1,3.2), для

47

которого точных аналитических решений даже в модели МЗ не получено. Точные аналитические результаты модели МЗ для переходного тока в случае экспоненциального распределения и некоторых других модельных распределений ловушек приведены в гл. 5.

1.5. Прыжковый транспорт

1.5.1. Уравнение баланса

Взаимодействие электрона со случайным потенциалом неупорядоченной среды, в котором он локализован, очевидно, нельзя считать слабым и описывать изменения состояния носителя со временем кинетическим уравнением Больцмана [1:2]. Строгий подход к теоретическому исследованию прыжковой кинетики носителей заряда состоит в решении уравнения баланса для среднего числа за-

полнения локализованного состояния (ЛC) λ , fλ (t ) [1:5]:

заполненного состояния λ в свободное состояние λ' . Первый член в правой части уравнения (1.48) описывает темп прихода носителей на состояние λ с других состоянийλ' , второй – темп ухода с состояния λ на окружающие свободные состояния λ' . Уравнение (1.48) описывает переходы ферми-частиц. Например, множитель (1− fλ ) даёт вероятность того, что состояние λ свободно. Уравне-

ние (1.48) справедливо, если характерное время изменения функции fλ достаточно велико: τ >> , где – характерное измене-

ние энергии при переходах между ЛС [1:5]. Это условие легко выполнимо в случае туннельных переходов между сильно локализованными состояниями с участием фононов (см. раздел 1.5.2).

48

Согласно принципу детального баланса, каждое из слагаемых в правой части уравнений (1.42) и (1.43) обращается в нуль в состоянии термодинамического равновесия. При этом решением уравнения (1.48) является функция Ферми,

а решением (1.49) – функция распределения Больцмана, fB (Eλ ) exp(−Eλ kT ). Нетрудно убедиться, что принцип детального баланса выполнен при условии

согласно которому вероятность перехода вверх по энергии (случай Eλ' > Eλ ) экспоненциально меньше, чем вниз.

Следует рассмотреть вопрос об описании процессов переноса (транспорта) носителей заряда при помощи (1.48). Электрическое поле или градиент концентрации носителей заряда нарушают баланс прихода и ухода носителей на произвольное состояние. Плотность тока через любое макроскопическое сечение (имеющее коор-

динату z = z0 , ось z направлена вдоль поля) можно записать как

разность темпов переходов (отнесённых к площади сечения S) носителей заряда через это сечение слева (носители прыгают с со-

стояний с координатами zλ < z0 на состояния с координатами zλ' > z0 ), и, напротив, справа [1:5]:

В стационарных условиях плотность тока не зависит от координаты. Выражение (1.52) можно упростить, формально усреднив его

по координате z0 :

(1.53)

49

где Ω = SL – объём образца. Электрическое поле напряжённости F, во-первых, изменяет энергии ЛС за счёт добавления электростатической энергии −eFzλ и, во-вторых, приводит к отклонениям чисел

заполнения состояний от их равновесных значений: fλ = fF + δfλ .

Чтобы вычислить плотность тока, необходимо найти функцию распределения носителей по состояниям λ , т.е. решить уравнение (1.48). Понятно, что для больших систем это является очень громоздкой вычислительной задачей, особенно если распределение fλ

зависит от времени и пространственных координат. Дополнительная сложность связана с тем, что далеко не всегда в неупорядоченных системах отклонения от равновесия (т. е. поправки δfλ ) можно

считать малыми (например, если начальное распределение фотогенерированных носителей далеко от равновесного). Поэтому большое распространение получило, с одной стороны, численное моделирование Монте-Карло, с другой – приближённые методы, некоторые из которых рассматриваются далее. Вычисление частот перехода νλλ' , входящих в уравнения (1.48), (1.49) – также очень не-

простая задача, поскольку свойства случайного потенциала и точный вид волновых функций локализованных носителей в неупорядоченных органических материалах, как правило, неизвестны. К счастью, для вычисления основных зависимостей νλλ' от энергий

этих состояний, Eλ и Eλ' , и расстояния между ними, r , доста-

точно знать асимптотику волновых функций на больших расстояниях от центра локализации (см. раздел 1.5.2).

1.5.2. Переходы между локализованными состояниями

В неупорядоченной среде вероятность того, что разные состояния имеют одинаковые энергии, строго говоря, равна нулю, что, казалось бы, исключает туннельные переходы между ними. Для того чтобы туннельный переход между ЛС осуществился, разность их энергий надо компенсировать за счёт взаимодействия носителя с колебаниями окружающих атомов (молекул), иначе говоря, за счёт испускания или поглощения одного или нескольких фононов. Таким образом, для нахождения частот νλλ' надо рассматривать элек-

50