
Никитенко Нестационарные процессы переноса и 2011
.pdf
ванном интервале α . Это естественно, так как модель НТ, в отличие от СНТ, непосредственно учитывает вклад в проводимость носителей заряда, занимающих мелкие ловушки, что существенно при высоких температурах (то есть больших α ) даже в случае дисперсионного транспорта, характерного для экспоненциально распределённых ловушек.
|
|
|
|
|
Таблица 5.1 |
|
jμ j |
|
|
|
|
α |
jτ j |
tFμ tF |
tFτ tF |
ν0tmin |
|
|
0,82 |
|
|
|
|
0,3 |
1,17 |
1,41 |
0,78 |
1,2 |
|
0,5 |
0,79 |
1,57 |
1,27 |
0,64 |
3,5 |
0,7 |
0,82 |
2,72 |
1,16 |
0,49 |
23 |
0,9 |
0,92 |
9,15 |
1,05 |
0,29 |
90000 |
Однако приближённая временная зависимость функции θ1 (t),
см. уравнение (5.14), из которой следует чисто степенная зависимость тока от времени до пролёта в НТ и «точной» моделях, см. уравнения (5.16) и (5.20) соответственно, и на которой основаны расчёты, результаты которых отражены в табл. 5.1, в действительности имеет нижний (по времени) предел применимости tmin . Это
время резко растёт с ростом α и при α ≤1 намного превышает v0−1 , см. последнюю колонку в табл. 5.1 (указанное выше не относится к функции τ(t) и, соответственно, к результатам модели
СНТ, которая при любых значениях α приводит к простой степенной зависимости (5.15)). Действительно, более точная, чем (5.14), аппроксимация уравнения (5.11) приводит к следующему выражению
θ1 (t )≈ |
1 −α |
(v0t ) |
−(1−α) |
−Γ(α) |
−1 |
(v0t ) |
−(1−α) |
, v0t 1. |
(5.25) |
α |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
Дело в том, что в случае α ≤1 второе слагаемое в квадратных скобках в (5.25) убывает медленно. Оно составляет долю меньше
201

чем η<1 от 1 при условии
t > tmin = v0 |
−1 ηΓ(α) −1 (1−α) , η = 0,3. |
(5.26) |
Значение η = 0,3 выбрано, исходя из результатов численных расчётов. Значения tmin приведены в табл. 5.1. Именно при выпол-
нении условия (5.26) аналитические результаты для переходного тока, приведённые выше, достаточно точны.
Подстановка уравнения (5.25) вместе с (5.13) в уравнения (5.3), (5.4) приводит к более точным, чем (5.16)–(5.19), аналитическим выражениям для переходного тока в бездиффузионном НТ – приближении:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α −(v0t )α−1 Γ(α) |
|
−1 |
|
|
||||||||||
|
|
|
j (t ) |
j0 = (1 −α)(v0t )α−1 |
|
|
|
, v0 |
t ≤ t , (5.27) |
|||||||||||||||||||
|
|
|
Γ(1+ α)F (t )2 |
|
|
|
||||||||||||||||||||||
|
( |
|
) |
0 |
|
|
( |
|
) |
( |
|
) ( |
|
) |
|
( |
|
) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
α−1 F −1 |
|
|
|
|
|
|
|
|
|
||||||||||||
j |
|
t |
j |
= 1 |
−α |
|
Γ |
1 + α |
|
v t |
|
|
t |
|
× |
|
|
|
|
|
|
|
||||||
× 1 |
− t t |
0 |
(t ) |
α−1 |
F t |
0 |
(t ) |
F |
(t )−(1 − α)(1 −t |
0 |
(t ) t ) |
F (t ) , |
t > t , |
|||||||||||||||
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
* |
|||
|
|
|
F (t)=1−(v0t )α−1 |
Γ(α). Хотя уравнения (5.27), |
|
(5.28) |
||||||||||||||||||||||
где |
(5.28) сущест- |
|||||||||||||||||||||||||||
венно упрощают вычисления в сравнении с (5.3), (5.4), найти аналитическое приближение к t* и t0 (t), подобные (5.18) и (5.19), к
сожалению, не удаётся, так что эти времена определяются трансцедентными уравнениями (5.5).
Таким образом, вопрос о применимости различных моделей требует проведения численных расчётов. На рис. 5.6 приведены результаты вычислений согласно НТ-модели (с учётом СПД, урав-
нения (5.1), (5.12), (5.13)) и СНТ-модели (уравнение (2.14)), см. со-
ответственно сплошные и пунктирные кривые, для нескольких значений α . Сравнение кривых подтверждает сделанный ранее вывод о том, что СНТ-модель даёт значительно меньшие значения времени пролёта в сравнении с НТ-моделью, особенно при α > 0,5. Так, при α = 0, 4 СНТ и НТ модели дают значения безразмерного вре-
мени пролёта v0tF , равные соответственно 1 107 и 1,5 107 (разница
202

в 1,5 раза), при α = 0,6 – 7 104 и 3 105 (разница в 4 раза), при α = 0,9 – 2 103 и 2 104 (разница в 10 раз!) В случае α = 0,9 как до,
так и после времени пролёта кинетика тока является более сложной, чем простая степенная зависимость, в согласии с уравнениями (5.27), (5.28), поскольку время tmin в этом случае превышает время
пролёта. Следует отметить, что на довольно длительном после пролёта интервале времени ток падает по закону, который близок к степенному, но средний показатель по абсолютной величине значительно превышает 1 + α . Следовательно, сумма показателей степенных законов спада тока до и после пролёта будет значительно меньше 2 при достаточно высоких температурах. При значительном превышении времени пролёта обе модели дают приближение к асимптотическому закону (5.21).
100 |
|
|
|
|
|
|
10-1 |
|
3 |
|
|
|
|
10-2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
10-3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
j / j |
|
|
|
|
|
|
10-4 |
|
|
|
|
|
|
10-5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
10-6 |
|
|
|
|
|
|
102 |
103 |
104 |
105 |
106 |
107 |
108 |
|
|
|
ν0t |
|
|
|
Рис. 5.6. Временные зависимости переходного тока для нескольких значений дисперсионного параметра α: 1 – 0,4; 2 – 0,7; 3 – 0,9. Значения других парамет-
ров: L = 20 мкм, |
F = 5 107 |
В/м, |
v |
=106 с-1, τ |
μ |
0 |
= 2,5 10−16 |
м2/В. Сплошные кри- |
|
0 |
|
0 |
0 |
|
|
|
вые рассчитаны в рамках НТ-модели, пунктирные – в рамках СНТ-модели согласно уравнению (2.14)
Рис. 5.7 содержит временные зависимости переходного тока, рассчитанные согласно различным моделям на начальном (до пролёта) интервале времени при α = 0,9. Хотя приближение СНТ
(кривая 3) и дает правильный предельный переход
203

j (t) → j0α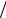 (1+α), v0t 1, (модель НТ приводит к величине, которая в 2 раза меньше), именно модель НТ на важнейшем практически временном интервале v0t >1 даёт хорошее согласие с резуль-
(1+α), v0t 1, (модель НТ приводит к величине, которая в 2 раза меньше), именно модель НТ на важнейшем практически временном интервале v0t >1 даёт хорошее согласие с резуль-
татом численного решения уравнений РФВ (1.18)–(1.20) [5:5], см. кривую 1 на рис. 5.7, в отличие от СНТ. Последняя модель даёт ложный максимум при v0t ≥1 , который, впрочем, практически не-
заметен в случае α ≤ 0,5. Пунктирные кривые на рис. (5.6), пред-
ставляющие результат счёта по приближённому уравнению НТмодели (5.27), дают, как и следовало ожидать, практически точное совпадение с результатом более точных уравнений (5.3), (5.10), (5.11) при v0t ≥ 3 .
j / j 0
100 |
|
3 |
|
|
|
2 |
1 |
|
|
|
|
10 |
-1 |
|
4 |
|
|
|
|
10-2 














































































 10-2 10-1 100 101 102 103 104 105 106
10-2 10-1 100 101 102 103 104 105 106
ν0t
Рис. 5.7. Сравнение результатов различных моделей на начальном интервале времени в случае α = 0,9 . Значения других параметров те же, что и на рис.5.5. 1–
численное решение уравнений РФВ [5:5], 2 – модель НТ, 3 – СНТ, 4 – асимптотический закон (5.19)
Наконец, на рис. 5.8 сравниваются результаты вычислений при v0t 1 для α = 0,5; 0,7; и 0,9 в НТ-модели с учётом СПД, см. урав-
нения (5.1), (5.12), (5.13), (сплошные кривые), более точной (уравнения (5.5), (5.27) и (5.28)) и приближённой (уравнения (5.16)– (5.19)) бездиффузионных моделей (соответственно, пунктирные и точечные кривые). Как видно из рисунка, бездиффузионное при-
204

ближение даёт хорошее совпадение с вариантом НТ-модели, который учитывает СПД, при всех временах, кроме сравнительно короткого интервала вблизи времени пролёта). Таким образом, более простой вариант НТ-модели, не учитывающий СПД (как и обычную диффузию), может успешно применяться при моделировании временных зависимостей переходного тока, контролируемого экспоненциально распределёнными ловушками, а время излома кривой ttr , см. уравнение (5.5б), служит хорошим приближением для
времени пролёта при α ≥ 0.5 . Ещё более простой вариант бездиф- |
||||||||
фузионной НТ – модели, см. уравнения (5.16)–(5.19), даёт количе- |
||||||||
ственно точные результаты при α ≤ 0,7 , |
v0t |
1. |
||||||
|
10-1 |
|
|
3 |
|
|
|
|
|
10-2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
-3 |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
j / |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
10-4 |
|
|
|
|
|
|
|
|
10-5 |
|
|
|
|
|
|
|
|
|
102 |
103 |
104 |
105 |
106 |
|
107 |
ν0t
Рис. 5.8. Сравнение результатов НТ-модели с учётом (сплошные кривые) и без учёта (пунктирные кривые) СПД, а также результатов упрощённой НТ-модели (точечные кривые), см. уравнения (5.16) – (5.19), для нескольких значений α : 1– 0,5; –0,7; 3– 0,9. Значения других параметров те же, что и на рис. 5.6
При α > 0,7 эта модель несколько завышает время пролёта (при α = 0,9 – в 2 раза). Простейшее СНТ– приближение даёт количественно верные результаты при α ≤ 0,5. В то же время при α > 0,7
эта модель даёт неточные результаты, поскольку её применимость сильно нарушена (исключая асимптотический режим, когда время много больше времени пролёта). Следует отметить качественное согласие приведённых выше результатов для переходного тока с данными численных расчётов работ [5:6, 7].
205
Обычно отличительным признаком экспоненциального распределения ловушек считается степенной закон спада с показателем
−(1−αi ) до времени пролёта и также степенной закон с показателем −(1+αf ) после времени пролёта, при этом αi = αf = α = kT E1 .
E1 .
Однако, применение более точной, чем СНТ, модели неравновесного транспорта (НТ) показывает, что спад переходного тока в случае α ≥ 0,7 как до, так и после пролёта происходит по закону, бо-
лее сложному, чем простая степенная зависимость. Попытки аппроксимации переходного тока степенной функцией на не слишком широких интервалах времени до и после времени пролёта показывают, что αf > αi при kT E1 > 0,8 . При kT
E1 > 0,8 . При kT E1 ≥ 0,9 в случае
E1 ≥ 0,9 в случае
времён, меньших времени пролёта, может даже быть сделан вывод о квазистационарности, поскольку 1 −αi 1. Подобное поведение
переходного тока было отмечено ранее для случая гауссовского распределения ловушек по энергии [1:14]. Определение времени пролёта, исходя из пересечения асимптотик временной зависимости тока, построенной в двойных логарифмичесих координатах, теряет смысл при α ≥ 0,8 , поскольку последние уже не являются
больше прямыми (кривая 3, рис. 5.8).
Таким образом, при достаточно высоких температурах переходный ток, контролируемый многократным захватом носителей заряда на ловушки, экспоненциально распределённые по энергии, обнаруживает временную зависимость, близкую к той, которая считается характерной для гауссовского распределения ловушек по энергии. Поэтому изучение энергетического распределения ЛС в случае слабо неравновесного транспорта ( α ≥ 0,7 ) времяпролёт-
ным методом требует повышенной осторожности, в частности детального анализа зависимости времени пролёта от температуры и толщины образца.
5.4. Прямоугольное распределение
Вывод уравнения, описывающего полевую диффузию, как в квазиравновесном [3:33], так и в неравновесном [3:27, 28] режимах
206

переноса является приближённым. В данном разделе для оценки точности сделанных приближений выполнено сравнение с точными результатами для переходного тока в условиях ВПМ, которые были получены в рамках модели МЗ для прямоугольного распределения ловушек [5:8]. Это распределение ловушек задано следующими
уравнениями: g (E) =1 Emax , Etrans − E ≤ Emax ; g (E ) = 0 ,
Emax , Etrans − E ≤ Emax ; g (E ) = 0 ,
Etrans − E > Emax . Уравнения (1.35), (4.3) приводят к следующим выражениям для квазиравновесной подвижности и коэффициента по-
левой диффузии: μeq = μ0 τ0 (αtmax ) , |
DFeq =(μeq F0 )2 tmax 2 , где |
|
α = kT Emax , tmax = v0 |
−1 exp[Emax kT ] – |
максимальное время осво- |
бождения носителей с ловушек. В работе [5:8] при условиях α 1
и t t f , где t f = L μ0 F0 |
– время пролёта квазисвободных электро- |
||||||
нов, получено: |
|
|
|
|
|
|
|
|
j (t ) |
|
t f |
αN |
(t tmax )y |
|
|
|
|
= |
|
exp (−t trel ) ∫ dy |
Γ(y) |
, |
(5.29) |
|
j |
t |
|||||
0 |
|
|
0 |
|
|
|
|
где j0 =σ0 μ0 F0e L – начальное (после импульсной генерации) значение плотности тока, N = t f
L – начальное (после импульсной генерации) значение плотности тока, N = t f  τ0 – среднее число захватов квазисвободных носителей ловушками в процессе их дрейфа через слой.
τ0 – среднее число захватов квазисвободных носителей ловушками в процессе их дрейфа через слой.
В уравнении (5.29) |
y = αNx L . В типичном случае |
αN 1 инте- |
||
грал «набирается» |
при значениях y 1 , если t > trel . Используя |
|||
формулу |
Стирлинга для гамма-функции |
при |
y 1 , |
|
Γ(y)≈ (2π |
y)1 2 exp(−y)yy , можно аппроксимировать подыинте- |
|||
гральное выражение следующим образом:
(y 2π )1
2π )1 2 exp{y 1 − ln (y
2 exp{y 1 − ln (y y0 ) } .
y0 ) } .
Это выражение имеет максимум при y = y0 = t tmax . Разложение в степенной ряд в окрестности y0 даёт следующее приближённое выражение:
tmax . Разложение в степенной ряд в окрестности y0 даёт следующее приближённое выражение:
j (t )≈ |
eσ |
0 |
L |
|
x |
1 2 |
|
(x −μeq F0t )2 |
|
|
|
∫ |
dx |
|
|
exp − |
|
|
, |
||
|
|
|
|
|||||||
|
Lt |
|
|
|
|
4DFeqt |
|
(5.30) |
||
|
0 |
|
2πμeq F0tmax |
|
|
|||||
207

Оценка x ≈ μeq F0t в предэкспоненциальном множителе и интег-
рирование |
в |
уравнении (5.30) приводит при |
условии |
μeq F0t 2 |
DFeqt , |
т.е. t 2tmax , к уравнению (2.6) с |
D = DFeq и |
μ = μeq . Следует заметить, что условие t > tmax , использованное при
выводе уравнения (5.30), является условием установления квазиравновесного режима переноса [5:8], для которого и справедливо уравнение (2.6).
1,0 |
|
|
3 |
|
|
|
|
|
|
st |
1 |
|
|
|
j / j |
2 |
|
|
|
0,5 |
|
|
|
|
|
t0 |
|
t1/2 |
|
0,0 |
|
|
|
|
0 |
1x105 |
2x105 |
3x105 |
4x105 |
|
|
t / tf |
|
|
Рис. 5.9. Зависимости переходного тока от времени в случае прямоугольного распределения ловушек по энергии, вычисленные согласно уравнениям (5.29) и (2.6), см. сплошные и штриховые кривые соответственно. Плотность тока и время нор-
мированы величинами jst = e(σ L)μeq F0 и t f = L
L)μeq F0 и t f = L μ0 F0 соответственно. Штрихпунктирные прямые показывают способ определения характерных времён t0 и t1/ 2 для кривой 1. Значения L, мкм: 1 – 0,1; 2 – 1; 3 – 3. Остальные парамет-
μ0 F0 соответственно. Штрихпунктирные прямые показывают способ определения характерных времён t0 и t1/ 2 для кривой 1. Значения L, мкм: 1 – 0,1; 2 – 1; 3 – 3. Остальные парамет-
ры: μ0 =10−5 м2 В-1 с-1, τ0 =10−10 с, ν0 =106 с-1, Emax  kT = 5
kT = 5
В случае прямоугольного распределения ловушек времена окончания сильно неравновесного (дисперсионного) режима и начала квазиравновесного режима переноса совпадают, teq _ μ =teq _ D =tmax . Другими словами, временной интервал квази-
дисперсионного транспорта практически отсутствует, по причине резкого «обрыва» распределения при больших энергиях.
208

На рис. 5.9 приведены кривые переходного тока, вычисленные для нескольких значений толщины слоя L согласно уравнению (5.29) и приближённому уравнению (2.6), см. сплошные и пунктирные кривые, соответственно. Если кривая 1 отвечает пролёту в режиме сильно неравновесного транспорта, то при увеличении L (и времени пролёта) форма кривой, как и следовало ожидать, всё более приближается к результату уравнения (2.6), см. кривые 2, 3. По данным вычислений определены значения параметра W , и согласно уравнениям (2.3) и (2.9), определён коэффициент стимулированной полем диффузии, а также значения eDFeq  kTμeq , которые
kTμeq , которые
показывают, во сколько раз отношение DFeq  μeq превышает вели-
μeq превышает вели-
чину kT e , т.е. результат соотношения Эйнштейна. Результаты приведены в табл. 5.2.
e , т.е. результат соотношения Эйнштейна. Результаты приведены в табл. 5.2.
|
|
|
|
|
|
|
Таблица 5.2 |
|
L , мкм |
W |
|
eDFeq |
|
DFeq 10−12 м2/с |
W ' |
D 'Feq 1012 м2/с |
|
|
|
|
μeq kT |
|
|
|
|
|
|
|
|
|
|
|
7,4 |
|
|
0,3 |
0,53 |
10,73 |
|
9,0 |
0,48 |
|
||
1,0 |
0,30 |
11,46 |
|
9,6 |
0,29 |
9,0 |
|
|
3,0 |
0,17 |
11,04 |
|
9,3 |
0,17 |
9,3 |
|
|
Согласно данным табл. 5.2, DFeq  μeq >> kT
μeq >> kT e . Таким образом, пренебрежение обычной диффузией оправдано. Значения DFeq , определённые из графиков, следует сравнить с теоретическим значением, которое составляет 8, 42 10−12 м2/c. При этом надо учитывать погрешности, связанные с неточностью нахождения параметра W .
e . Таким образом, пренебрежение обычной диффузией оправдано. Значения DFeq , определённые из графиков, следует сравнить с теоретическим значением, которое составляет 8, 42 10−12 м2/c. При этом надо учитывать погрешности, связанные с неточностью нахождения параметра W .
Величину погрешностей иллюстрирует разброс величин DFeq′, вы-
численных по значениям W ′, которые определены по графикам, построенным на основе уравнения (2.6). Эти величины должны совпадать с теоретическими значениями DFeq , поскольку они ис-
пользованы при вычислениях этих графиков (см. пунктирные кривые на рис. 5.9). Как видно из данных таблицы, расчётные и теоре-
тические величины DFeq совпадают в пределах погрешности. Та-
ким образом, результаты вычислений согласуются как с теорией, так и с аналитическими оценками, приведёнными выше.
209
ГЛАВА 6. КИНЕТИКА БЛИЗНЕЦОВОЙ РЕКОМБИНАЦИИ В РЕЖИМЕ НЕРАВНОВЕСНОГО ТРАНСПОРТА
6.1. Аналитическое описание близнецовой рекомбинации
врежиме дисперсионного транспорта
6.1.1.Постановка задачи
Транспорт носителей заряда в неупорядоченном материале на длительном временном интервале является неравновесным. В данной работе рассмотрен случай полимеров с экспоненциальным распределением ловушек (1.42) и достаточно сильным беспорядком, α = kT E1 ≤ 0,5 , что справедливо в свете данных НРЭ для вы-
E1 ≤ 0,5 , что справедливо в свете данных НРЭ для вы-
сокоомных полимеров с неполярными молекулами, таких как полиэтилентерефталат (ПЭТФ), ПС, ПЭВД, полипропилен (ПП), ПТФЭ и др. [1:13]. Поэтому оправдано применение приближения сильно неравновесного транспорта (называемого также τ− моделью) для анализа переноса «близнецов». Ограничения применимо-
сти данной модели в случае произвольного g (E ) рассмотрены в
следующем разделе. Аналог уравнения Смолуховского (см. уравнения (1.14) и (1.90)), в СНТ-приближении представляет собой уравнение (1.40) гл. 1, которое наряду с однородным полем с напряжённостью F0 включает и кулоновское поле [6:1, 2],
|
|
e |
|
er |
|
|
|
|
|
|
D τ(t )div gradρ(r,t )+ |
|
|
|
−F |
|
ρ(r,t ) |
− |
|||
|
|
|
3 |
|||||||
0 |
|
kT |
4πεε |
r |
0 |
|
|
|||
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
−ρ(r,t )= −ρ(r,0). |
|
|
|
(6.1) |
|||||
В уравнении (6.1) ρ(r,t )– пространственно-временная функция
распределения основного носителя заряда, радиус-вектор которого r отсчитывается от менее подвижного заряда противоположного знака (для определенности, электрона).
Хотя в неупорядоченных органических материалах наиболее распространена изотропная проводимость ( d = 3 ), известен ряд полимеров, в которых перенос заряда происходит преимущественно в выделенной плоскости ( d = 2 ) или вдоль выделенного направления ( d =1 ). При этом квантовый выход близнецовой рекомбинации
210
