Никитенко Нестационарные процессы переноса и 2011

случайно близких молекул. Мотт [1:3] оценил масштаб энергетического разброса как V0 = I0 exp(−γr), а ширину зоны – как

B = 2zI0 exp(−γr2 ), где r2 = (N2)−13 – среднее расстояние между

парами. Далее, используя критерий локализации Андерсона и считая критическую величину V0 B равной 2, z = 6 , Мотт оценил

критическое значение величины γN −13 как 5. Анизотропия волно-

вых функций может привести к меньшим значениям z, откуда следует меньшее критическое значение, 2,5.Численные расчёты также свидетельствуют о меньших величинах, 3–4 [1:4]. Надо заметить,

что величина γN −13 = 5 типична для органических материалов.

1.3.3. Край подвижности и минимальная металлическая проводимость

Если критерий Андерсона не выполнен, локализация всётаки имеет место в «хвостах» зоны состояний g (E ) (см. правую часть

рис. 1.5), хотя состояния в центре зоны остаются делокализованными. Если параметр V0 B , уменьшаясь, переходит через критиче-

ское значение, делокализованные состояния появляются сначала в середине зоны, где отклонения энергий от среднего значения малы и вероятность существования сколь угодно длинной цепочки состояний таких, что энергии соседей в изолированных ямах, e1 и e2, отличаются не более чем на 2I, максимальна. В то же время со-

стояния в «хвостах» зон, с энергиями e >> B , пусть малочислен-

ные, останутся локализованными, поскольку их энергии отличаются от энергий соседних состояний более чем на 2I. Волновая функция делокализованных состояний является суперпозицией очень большого числа волновых функций изолированных ям, см. уравнение (1.1) и рис. 1.6, а, причём эти функции входят с примерно одинаковым (хотя и меняющимся от узла к узлу) весом. В случае локализации носителя на некотором узле волновые функции других узлов входят в общую волновую функцию с весом, который экспо-

ненциально убывает ( exp(−γr)) по мере удаления от данного узла (см. рис. 1.6, б). Критическая энергия Ec , которая отделяет ло-

31

кализованные состояния от делокализованных, называется краем подвижности. На существование такой энергии впервые указал Мотт [1:4]. Мотт предложил и критерий локализации всех состояний с данной энергией, который может быть проверен экспериментально (см. ниже) – это обращение в ноль проводимости при дан-

ной энергии, GE (E,T ), при стремлении температуры T к абсолютному нулю. Интегрирование функции GE (E,T ) по энергии вместе с производной от функции распределения носителей по энергии (функции Ферми), ∂f (E)∂E , даёт полную проводимость G .

Понятие края подвижности играет фундаментальную роль в физике неупорядоченных неорганических материалов. Оно в некоторой степени позволяет применять к этим материалам концепции разрешённых и запрещённых зон, несмотря на то, что запрещённые зоны могут и отсутствовать (рис. 1.7).

E

EC

EF

EV

g (E )

Рис. 1.7. Локализованные (короткие чёрточки) и делокализованные (длинные линии) состояния. Пунктирные стрелки показывают перенос электрона между ловушками через зону делокализованных состояний

Хотя в любом интервале энергий могут быть состояния для носителей заряда, в некоторой области (которая лежит между краями подвижности для дырок и электронов, EV и EC ) все состояния ло-

кализованы. Поэтому данный интервал энергий называют щелью по подвижности. Если концентрация локализованных состояний в этой щели достаточно мала (и температура достаточно велика),

32

чтобы исключить электропроводность посредством туннельных прыжков между ними, состояния в щели являются ловушками для носителей заряда. Локализованные на ловушках носители могут участвовать в проводимости только после термической активации в зону делокализованных состояний, практически – в тонкий (не шире kT) слой состояний вблизи края подвижности. Поэтому, например, темновая электронная проводимость зависит от температуры по закону Аррениуса,

где EF – энергия Ферми (см. рис. 1.7), т.е. материал является ди-

электриком или полупроводником, хотя плотность состояний вблизи уровня Ферми отлична от нуля. В этом случае неупорядоченный материал называют ферми-стеклом. Если энергия Ферми может

возрастать до значений, больших EC (из-за изменения состава,

давления или какоголибо другого параметра), то при пересечении края подвижности произойдёт переход от полупроводниковой проводимости к проводимости металлического типа, известный как переход Андерсона. При низких температурах он проявляется в резком увеличении проводимости от величины, близкой к нулю, до величины Gmin [1:4]. В уравнении (1.7) Gmin – это величина GE при

E = EC , которую, согласно Мотту, принято называть минимальной металлической проводимостью. При нулевой температуре, когда состояния вплоть до E = EF заполнены электронами, Gmin является

минимальной ненулевой величиной, которую может иметь проводимость данного материала. Величину минимальной металлической проводимости можно оценить, используя модель Андерсона.

μ = (e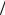kT )D (см. раздел 1.5), где D = L2 6t – коэффициент диффузии, L – длина свободного пробега, t B – типичное время пере-

скока (оценка из соотношения неопределённости). В критическом случае надо взять минимальное значение длины пробега, которое,

33

как заметили ещё Иоффе и Регель [1:23, 3, 4], порядка постоянной

мальная металлическая проводимость определяется только универ-

ханические оценки и экспериментальные данные дают значения

метить, что вопрос о существовании перехода Андерсона в двумерных системах до сих пор не вполне ясен. Есть теоретические результаты о локализации всех состояний в двумерной бесконечной неупорядоченной системе [1:24, 25]. Экспериментальные данные, вроде бы свидетельствующие о наличии такого перехода, могут быть интерпретированы по-разному. Может быть, происходит лишь переход к проводимости по слабо локализованным состояниям, которую трудно отличить от «настоящей» металлической проводимости в образцах малого размера (см. обзор [1:25]). Возможно, необходимо учитывать кулоновское взаимодействие между носителями заряда.

Следует ожидать, что радиус локализации волновых функций стремится к бесконечности, если энергия приближается к краю подвижности. Такое поведение даёт известный квантовомеханиче-

s =1/ 2 . Более точные расчёты, учитывающие случайный характер потенциала в окрестности каждой ямы, в согласии с экспериментом дают значения критического индекса s от 0,6 до 2/3 в трёхмерном

случае (при этом γ =const (EC − E)S вблизи края подвижности)

[1:4]. В органических материалах, как правило, все состояния локализованы, при этом γa0 >>1 (сильная локализация). Надо заметить, что и при наличии края подвижности (в неорганических неупоря-

34

доченных полупроводниках) характеристики транспорта обычно определяются достаточно глубокими состояниями, на которых носитель проводит большую часть времени, будучи сильно локализо-

ван. Радиус локализации, γ−1 , в этом случае определяется свойст-

вами молекулы. При моделировании прыжкового транспорта он обычно считается феноменологическим параметром, который не зависит от энергии локализованного состояния.

1.4. Модель многократного захвата

Как видно из предыдущего раздела, для неупорядоченных материалов, в том числе и органических, типично квазинепрерывное распределение локализованных состояний, широко распределённых по энергии. Локализованные состояния с достаточно низкой энергией для носителей заряда являются ловушками. Это значит, что локализованный носитель «выключен» из процесса переноса на болееменее длительное (но всё же конечное) время. Транспорт можно понимать как процесс переноса носителей между ловушками. Каким образом это происходит: или путём перескоков между ловушками (чаще – через цепочку промежуточных ЛС) – прыжковый транспорт, или путём термического освобождения носителя в зону делокализованных состояний с последующим захватом на другую ловушку? В органических материалах, как правило, реализуется первый путь, в то время как модель многократного захвата (МЗ) была развита [1:17, 26, 27] для второго случая, применительно к неорганическим неупорядоченным материалам, таким, как аморфные кремний, селен, халькогенидные стёкла (например, As2Se3). Однако, как будет показано далее, см. раздел 1.6.4 и гл. 3, формализм модели МЗ при некоторых ограничениях применим и к описанию прыжкового транспорта. Дело в том, что внутри определённой фракции локализованных состояний перескоки происходят адиабатически быстро, и подсистема таких состояний аналогична зоне проводимости (в случае дырок – валентной зоне). На ловушках же носитель надолго задерживается. Формализм модели МЗ существенно упрощает теоретическое описание прыжкового транспорта, особенно в случае процессов, зависящих от координат и времени.

35

силу симметрии) совпадает с точкой, где N (x,t ) максимальна, движется с постоянной скоростью:

−∞

При этом, будучи первоначально тонким, пакет расплывается со временем вследствие диффузии – его среднеквадратичная дисперсия возрастает по закону

disp (t )= (x −x)2 = x2 −x2 = 2Dt .(1.11)

Из уравнений (1.10), (1.11) очевидно, что disp (t )x(t ) t−12 .

Следует заметить, что уравнения (1.8) имеют стационарное решение, когда макроскопический перенос отсутствует, хотя заряженные частицы движутся в приложенном поле (направо), концентрация растёт таким образом, что этот дрейфовый ток компенсируется диффузионным током (налево), так что j = 0 :

Разумеется, данное решение может реализоваться лишь в ограниченной (полуограниченной) области пространства, иначе оно расходится.

Если носители заряда (пусть в первом приближении; в случае неупорядоченной среды – хотя бы в той области энергий, которая вносит наибольший вклад в перенос) находятся в состоянии термодинамического равновесия, справедливо следующее соотношение Эйнштейна [1:28]:

Эйнштейн рассматривал броуновское движение частиц в условиях термодинамического равновесия во внешнем силовом поле. Чтобы понять логику вывода соотношения (1.13) в несколько упрощённом виде [1:29], вспомним барометрическую формулу (част-

(молекулы), g – ускорение свободного падения. Заменив в последнем выражении однородное гравитационное поле на однородное

37

электрическое (которое действует на частицы с зарядом e), т.е. mg на eF , и h на −x (чтобы ось координат была направлена вдоль поля), получаем N (x)= N (0)exp(eFxkT ). Сравнивая последнее

выражение с (1.12), получаем соотношение (1.13). Заметим, что в общем случае следует заменить операцию ∂∂x в уравнении (1.8а)

на оператор дивергенции (div), а в (1.8б) – на оператор градиента (grad), так как плотность тока – вектор. Выразив напряжённость электростатического поля (вообще говоря – неоднородного) через

его потенциал, F (r)= −grad ϕ(r) , и, используя соотношение Эйнштейна, можно записать уравнение (1.8) в следующей форме:

Нарушения соотношения Эйнштейна в случае прыжкового транспорта в органических материалах и причины этого обсуждаются в разделе 1.5.4.

1.4.2. Система уравнений

Все состояния (для определённости – электронные) разделены на проводящие состояния с объёмной плотностью MC , энергиями

выше края подвижности EC , а также ловушки с объёмной плотностью M0 и энергиями E < EC . В данном разделе ограничимся слу-

чаем «плоской геометрии», когда пространственная неоднородность описывается лишь одной декартовой координатой x . Урав-

нение баланса для функции ρ(x, E,t ) – плотности носителей заря-

где N0 (x,t ) – плотность носителей в проводящих состояниях (так называемых свободных носителей), t – время, отсчитываемое от

38

момента импульсной генерации носителей, функция c(E) – сече-

ние захвата, нормированное на скорость, характеризует быстроту захвата носителя из проводящего состояния на ловушку с энергией вблизи значения E . Первый и второй члены в правой части (1.15) описывают захват и освобождение локализованных носителей, соответственно. Время жизни свободных носителей до захвата на ловушки определяется уравнением

(1.15) не рассматривать энергетические зависимости c(E) и g (E ) раздельно, полагая geff (E)= c(E)g (E)c0 . В дальнейшем энергетическую зависимость c(E) не учитываем, полагая c(E)= c0 . Тогда (1.15) можно переписать следующим образом:

(1.17)

где ν0 = MC M0τ0 – частота попыток освобождения носителя с ло-

вушки.

В режиме малого сигнала уравнение (1.17) упрощается:

стью свободных носителей и энергетической плотностью носителей на ловушках следующим уравнением:

−∞

Поскольку энергетическая область ловушек достаточно широка, нижний предел интегрирования по энергии в (1.19) и последующих

39

уравнениях считается бесконечным. Чтобы рассмотреть процессы переноса, систему уравнений (1.18), (1.19) следует дополнить также уравнением непрерывности, которое учитывает, что ток создаётся лишь свободными носителями:

∂N (x,t )∂t + μ0 F0 ∂N0 (x,t )∂x − D0 ∂2 N0 (x,t )∂x2 = 0 , (1.20)

где μ0 и D0 – соответственно подвижность и коэффициент диффузии носителей в проводящих состояниях («свободных» носителей); F0 – напряжённость электрического поля, которое в малосигналь-

ном режиме можно считать однородным. Уравнение (1.20) учитывает, что в процессе переноса участвуют только носители в проводящих состояниях. В модели МЗ подвижность свободных носителей μ0 , время их жизни до захвата на ловушки τ0 и частотный

фактор освобождения с ловушек ν0 являются феноменологиче-

скими параметрами. Если транспорт является прыжковым, их можно выразить через другие феноменологические параметры, характеризующие прыжковый транспорт (см. разд. 3.5). Обычно полагают, что коэффициент диффузии и подвижность связаны соотноше-

нием Эйнштейна, D0 = (kTe)μ0 , ограничения применимости кото-

рого к прыжковому транспорту обсуждаются в разделе 1.5.4. Уравнений (1.18)–(1.20) достаточно для анализа плотности элек-

тронов (или дырок) в условиях времяпролётного эксперимента (гл. 2). Если плотность генерированных носителей заряда достаточно велика, необходимо использовать уравнение (1.17) вместо (1.18). Вообще говоря, в этом случае необходимо учитывать влияние плотности объёмного заряда на напряжённость поля согласно уравнению Пуассона:

где P(x,t ) – объёмная плотность дырок. Вообще говоря, электри-

ческое поле неоднородно и нестационарно. Если присутствуют носители заряда разных знаков (биполярный транспорт), систему уравнений (1.15), (1.19), (1.20) необходимо дополнить соответствующими уравнениями для дырок, при этом в правой части урав-

40