Решение.

Возьмем шаг=0.2. Используя расчетные формулы Рунге-Кутта (9.3), найдем приближенное решение задачи Коши:

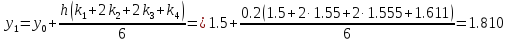
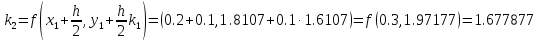
++)/6=2.14590898

Аналогично получаем 053228172

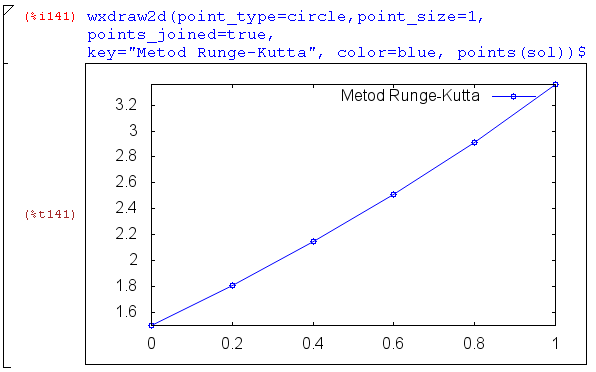
Таким образом, получили численное решение задачи Коши:

	0	0.2	0.4	0.6
	1.5	1.8107	2.14590898	2.511053228172

Графиком приближенного решения является ломанная, последовательно соединяющая точки ().

Реализация метода Рунге-Кутта с помощью системы Maxima

В системе Maxima для нахождения численного решения задачи Коши

методом Рунге - Кутта (четвертого порядка точности) есть встроенная функция . Для того, чтобы она стала активной, требуется подключить пакет dynamics с помощью команды:

Теперь задаем команду для нахождения решения:

Выполним построение найденного решения задачи средствами

пакета draw:

Точное решение поставленной задачи ищется в виде:

§10. Решение краевых задач для линейных дифференциальных уравнений второго порядка методом конечных разностей

Линейное дифференциальное уравнение второго порядка имеет вид

где 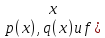) – некоторые, непрерывные на [a,b] функции. Краевая задача для линейного дифференциального уравнения состоит в нахождении его решения удовлетворяющего двухточечным линейным краевым условиям

где 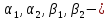постоянные и+,+

При решении этой задачи методом конечных разностей отрезок разбивают на равные части с шагом , где. Точки разбиения имеют абсциссы

,

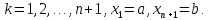
Значения в точках деления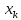искомой функции и ее производныхобозначим соответственно через,,.Заменяя производные правыми односторонними конечно-разностными отношениями для внутренних точек отрезкаприближенно будем иметь

,

Для концевых точек 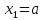и=bполагаем

и

Используя формулыдифференциальное уравнение (10.1) при

приближенно можно заменить системой линейных уравнений

,

Из формул краевые условиядополнительно дают еще два уравнения

B

Таким образом, получаем систему линейных уравнений с

неизвестными , представляющими собой значения искомой функции

Обозначим=,=,=. Выполнив алгебраические преобразования над уравнениями, можно привести систему к следующему виду:

Решив систему, получим таблицу значений искомой функции.

Пример Найти решение уравнениянас начальными условиями

Решение.

Из условия задачи и следует:

, ,,,,,,.

Разобьем отрезок [a,b] на равные части с шагом

Точки разбиения имеют абсциссы

Построим систему линейных алгебраических уравнений, где неизвестными являются.

Для коэффициентов основной матрицы системы для n-1 уравнений введем обозначения: ,,

Для коэффициентов последних двух уравнений введем обозначения,,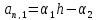

Для матрицы свободных членов введем обозначения:

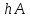= ,,k=1, 2, n =3, h=0.1

Остальные коэффициенты системы равны нулю.

Составим развернутую систему (10.5) для нашей задачи:

(

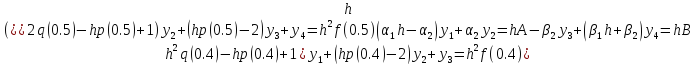
Представим систему в матричном виде:

=

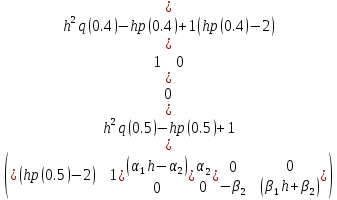Подставим значения переменных в систему:

=

=

После упрощения получим:

=

Решая полученную систему, найдем приближенное решение дифференциального уравнения:.

Реализация конечно-разностного метода

Выполним решение краевой задачи конечно-разностным методом в системе Maxima.

Вводим обозначения и задаем значения переменных:

Разбиваем отрезок [a ,b] на равные части с шагом .

Формируем список, содержащий все точки отрезка:

Сформируем пустую квадратную матрицу размера:

Теперь заполним матрицу, для заполнения коэффициентами первых двух уравнений системы воспользуемся циклом с параметром:

В двух последних уравнениях поменяем значения некоторых элементов с помощью оператора присваивания:

Теперь заполним столбец свободных членов:

Выведем полученные матрицы на экран:

Получили систему линейных уравнений, записанную в матричном виде , где— искомое решение. Найдем его матричным способом.