§ 7.Метод Эйлера

Простейшим численным методом решения задачи Коши для обыкновенного дифференциального уравнения является метод Эйлера, который еще называют методом ломанных Эйлера.

По оси введем равномерную сетку с шагом, т.е рассмотрим систему точек. Обозначим черезточное решение задачиа через- приближенные значения функцийв заданной системе точек.

Заменяя в уравнении производную в окрестности каждогого узла сетки разностным отношением приходим к уравнению:

Определение .Алгебраические соотношения между компонентами сеточной функции заменяемые исходными дифференциальными уравнениями в окрестности каждого узла сетки, называются разностными уравнениями.

Поэтому уравнение – разностное уравнение.

В окончательной форме можно определить по явной формуле

Геометрическая интерпретация метода Эйлера: интегральная кривая

на отрезкеприближается к ломанной, наклон которой определяется наклоном интегральной кривой уравнения в точке []. Рис.

Метод Эйлера относится к явным одношаговым методам. Вследствие систематического накопления ошибок метод используется редко или используется только для оценки вида интегральной кривой. Метод Эйлера называют методом Рунге-Кутта первого порядка точности.

Пример 7.1. Применяя метод Эйлера, найти решение задачи Коши в трех последовательных точках,,. Найти точное решение задачи и найти величину абсолютной погрешности в указанных точках.

Решение.

Возьмем шаг Используя расчетную формулу Эйлера, найдем приближенное решение задачи Коши:

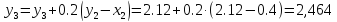
Таким образом, получили численное решение задачи:

	0	0.2	0.4	0.6
	1.5	1.8	2.12	2.464

Графиком приближенного решения является ломанная, последовательно соединяющая точки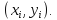

В этой задаче легко находится точное решение, например, методом вариации постоянной: 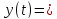0.5. Вычислим значения точного решения в указанных точках.

	0	0.2	0.4	0.6
	1.5	1.811	2.146	2.511

Абсолютную погрешность вычислим так: 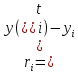. Тогда,,. Таким образом, максимальная величина погрешности равна

Реализация метода Эйлера с помощью системы Maxima

Зададим концы отрезка, на котором будем искать решение, и шаг:

Найдем количество точек разбиения отрезка с шагом

Сформируем два пустых одномерных массива размера для хра-

нения значения координат точек искомого решения:

Зададим начальное условие:

Заполним массив значениями, начиная сдос шагом. Для этого используем цикл с параметром.

Используя расчетную формулу Эйлера, заполним массив

Выведем полученное решение на экран:

Выполним построение ломаной Эйлера средствами пакета

Для нахождения точного решения задачи Коши воспользуемся встроенной командой Дифференциальное уравнение запомним под именем

Зададим начальное условие

Находим точное решение задачи Коши :

Вычислим значения функции в точках отрезка с шагом.

Найдем величину абсолютной погрешности:

§8.Метод Эйлера-Коши

Отличительная особенность метода Эйлера-Коши от метода Эйлера заключается в том, что значение в правой части уравнения вычисляется не только в точках сетки (шаг 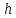), но и также в середине отрезков (шаг) (промежуточных точках).

Предположим, что промежуточное значениерешения задачи в точке

= , уже известно,вычисляются по следующим формулам:

, =

,

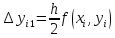Отсюда вычисляют

=

Геометрическая интерпретация метода Эйлера-Коши: определяется направление интегральной кривой в исходной точке и во вспомогательной точке,, а в качестве окончательного выбирается среднее из этих направлений. Метод Эйлера-Коши называют методом Рунге-Кутта второй точности.

Пример 8.1. Применяя метод Эйлера-Коши, найти решение задачи Коши в трех последовательных точках,,.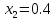