Глава 2. Численные методы приближенного решения задачи Коши для однородных дифференциальных уравнений в банаховом пространстве

§5. Общие сведения о дифференциальных уравнениях

При изучении физических явлений часто не удается непосредственно найти закон, связывающий независимые переменные и искомую функцию, но можно установить связь между этой функцией и ее производными, выражаемую дифференциальным уравнением. Приведём основные понятия теории дифференциальных уравнений [15].

ОпределениеУравнение, связывающее независимую переменную , искомую функциюи её производные, т.е уравнение вида

называется дифференциальным уравнением.

Здесьизвестная функция,- независимое переменное,неизвестная функция.

ОпределениеЕсли искомая функцияесть функция одной переменной, то дифференциальное уравнение называетсяобыкновенным.

ОпределениеПорядком дифференциального уравнения называется наивысший порядок входящих в него производных.

Определение 5.4. Решением дифференциального уравнения го порядка на интерваленазывается функция, определенная на отрезкевместе со своими производными дого порядка включительно, и такая, что подстановка функциив дифференциальное уравнение превращает последнее в тождество пона

Дифференциальное уравнение имеет бесконечно многорешений.

ОпределениеМножество всех решений уравнения называетсяобщим решением уравнения Всякое отдельно взятое решение называется егочастным решением.

Определение Задача для нахождения уравненияудовлетворяющего начальным условиям,,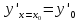…,, называетсязадачей Коши для уравнения

Известна теорема существования и единственности решения задачи Коши[12].

Теорема .Если в уравнении функция

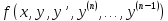
1. непрерывна по всем своим аргументам в некоторой областиих изменения;

2. имеет ограниченные в области частные производные

, ,,…,по аргументам

то найдется интервал на котором существует единственное решение, удовлетворяющее условиям

,…,где значенияy =,

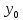,…,=содержатся в области.

§6. Численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка

Рассмотрим постановку задачи Коши для системы обыкновенных дифференциальных уравнений вида

=

где искомая вектор-функция;независимая переменная;

; ,

порядок системы;

–координаты;

.

Систему можно переписать в развернутом виде

где.

Если , то мы получаем обыкновенное дифференциальное уравнение первого порядка:

=

При этом решение задачи Коши для уравнения заключается в нахождении интегральной кривой, проходящей через заданную точку и удовлетворяющую заданному начальному условиюЗадача состоит в том, чтобы найти искомую функцию, удовлетворяющуюи заданным начальным условиям.

Построение численных алгоритмов решения уравнения опирается на дескритизацию задачи. Введем в области расчетадискретный набор точек,, в которых будем вычислять приближенное решение. Точкиназываются узлами интегрирования или узлами сетки, расстояние- шагом интегрирования или шагом сетки. Сеточной обастью (сеткой) называется савокупность всех узлов. Для характеристики точности численного метода определяется погрешность приближенного решения по формуле:

где значение точного решения в узле сетки.

Существует два класса методов для решения задачи

1. семейство одношаговых методов[15];

2. семейство многошаговых (m-шаговых) методов[15].

ОпределениеЧисленный метод называется явным, если вычисление решения в следующей точке осуществляется по явной формуле.

Метод называется одношаговым, если вычисление решения в следующей точке производится с использованием только одного предыдущего значения.

В дальнейшем будем рассматривать численные методы решения задачи Коши на примере уравнения первого порядка: