§4.Условия существования ограниченного решения у неоднородного уравнения

Рассмотрим неоднородное уравнение

с непрерывной функцией .

Предположим, что спектр оператора распадается на два спектральных множества. Обозначим черезиинвариантные подпространства оператора, соответствующие этим множествам и, черезисоответствующие спектральные проекторы.

Напомним, что [5]

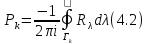
Определение 4.1 Функция вида

называется оператор – функцией Грина.

Она обладает следующими свойствами [12]:

1. При оператор – функциянепрерывно дифференцируема и удовлетворяет однородному уравнению

Этот факт непосредственно следует из.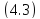

2. Скачок в нуле равен единичному оператору.

Действительно,

3. Вектор – функция

где непрерывна, удовлетворяет при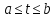неоднородному уравнению.

Для доказательства продифференцируем равенство

В дальнейшем, как правило, будем рассматривать случай, когда спектр не пересекается с мнимой осью (в частности, когда оператордихотомичен):.

Определение 4.2 Функцию Грина, определяемую формулой

назовем главной функцией Грина уравнения .

В формуле принимается,прии,при.

Поскольку спектр 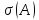не пересекается с мнимой осью, существуют числаи, при которых справедлива оценка [8]

Главная функция Грина играет важную роль при выяснении условий существования ограниченного на всей оси решения уравнения. В частности справедлива теорема [8]

Теорема 4.1. Для того чтобы любой ограниченный на всей оси непрерывной вектор – функции соответствовало одно и только одно ограниченное на всей оси решение уравнения необходимо и достаточно, чтобы спектрне пересекался с мнимой осью. Это решение дается формулой

где главная функция Грина уравнения.

Доказательство. Пусть любому ограниченному непрерывному соответствует ограниченное решение. Положимгдепостоянный вектор, и пустьединственное ограниченное решение уравнения

Вектор при любомтакже является решением этого уравнения, и в силу единственности, т.е., откуда.

Из произвольности следует, что линейный непрерывный операторотображает пространствоПо теореме Банаха (I.1.1)[1]такой оператор обладает непрерывным обратным оператором 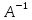, т.е. точкаявляется регулярной точкой оператора.

Пусть теперь произвольное чисто мнимое число. Рассмотрим уравнение

Подстановка дает

Повторяя проведенные выше рассуждения, получим, что оператор имеет непрерывный обратный оператор, т.е. регулярная точка.

Тем самым необходимость условия теоремы доказана. Для доказательства достаточности воспользуемся оценкой . Из этой оценки следует, что вектор – функция ограничена:

Тот факт, что эта функция удовлетворяет уравнению при

был установлен ранее [1].

Остается показать единственность ограниченного решения. Для этого достаточно проверить, что однородное уравнение не имеет ограниченных на всей оси решений, отличных от тривиального.

Допустим, что такое решение существует. Полагая,, его можно записать в виде

Поскольку спектром оператора в пространствеявляется множество, лежащее внутри левой полуплоскости, то первое слагаемое ограничено при, а значит, этим свойством обладает и второе слагаемое

Но тогда, учитывая тот факт, что спектр операторав пространстве(если он не пуст) лежит внутри правой полуплоскости, мы получим

Это неравенство при показывает, что. Аналогично показывается, что и при. Теорема доказана.