Решение.

Положим– шаг изменения пространственной переменной. Заменим частные производные в волновом уравнении конечно-разностными аппроксимациями

(x, y) = [],(x, y) =[].

Получим:

[] =].

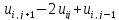Отсюда

+

Получили явную разностную схему, которая будет устойчивой если 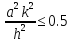. Отсюда k. Выберем

Построим алгоритм решения задачи:

Шаг 1.Вводим сетку:.Создаем нулевой массив значенийразмера m.

Шаг 2.Задаем значения

Шаг 3.Заполняем первую и вторую строки массиваграничными условиями,(нулевой начальной скорости соответствует совпадение значений (смещений) в первом и втором столбцах)

Шаг 4.Заполняем первый и последний столбец массива граничными условиями(на концах струны смещение равно нулю в любой момент времени).

Шаг 5. Находим решение , используя разностную схему

+

Также можно использовать и неявные разностные схемы. В этом случае частные производные заменяются конечно-разностными аппроксимациями, но не выражаются в явном виде через значения на предыдущих слоях. Для определенияна каждом временном шаге необходимо решать систему уравнений. При использовании неявных схем можно вести вычисления с достаточно большим шагом.

Преимущество неявных схем перед явными в том, что в неявных схемах шаг сетки можно сделать достаточно большим, не опасаясь, что ошибки округления «разрушат» решение.

Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima

Вводим сетку: . Создаем нулевой массив

Значений размера m.

Задаем значения

Заполняем первую и вторую строки массива U начальными условиями

( нулевой начальной скорости соответствует совпадение значений (смещений) в первом и втором столбцах).

Заполняем первый и последний столбец массива граничными усло-

виями (на концах струны смещение равно нулю в любой момент времени).

Находим решение, используя разностную схему

Для вывода полученного решения в виде поверхности преобразуем

наш массив в функцию двух переменных:

Теперь выполняем построение:

Заключение

В ходе исследовательской работы было изучено линейное дифференциальное уравнение с постоянным оператором в банаховом пространстве средствами функционального анализа, а также подробно рассмотрено решение задачи Коши.

Для достижения поставленной цели в данной работе была должным образом рассмотрена история возникновения и развития дифференциальных уравнений, подробно представлено решение однородного и неоднородного уравнения через операторную экспоненту, рассмотрены условия ограниченности однородного уравнения. Подробно изучено поведение решений на бесконечности в связи с характером расположения спектра оператора А.

Кроме того, в работе были рассмотрены практические методы решения задачи Коши для дифференциальных уравнений в банаховом пространстве. Очень подробно рассмотрены методы Эйлера, Эйлера-Коши и Рунге-Кутта. Выяснили, например, что отличительная особенность метода Эйлера-Коши от метода Эйлера заключается в том, что значение в правой части уравнения вычисляется не только в точках сетки, но и также в середине отрезков (промежуточных точках), а также решения задачи Коши, полученные методом Эйлера и методом Эйлера-Коши очень близки.

Кроме того, было подробно описано решение краевых задач для линейных дифференциальных уравнений второго порядка методом конечных разностей. Рассмотрен метод сеток для решения дифференциальных уравнений в частных производных.

Разработан вычислительный алгоритм реализаций решений дифференциальных уравнений и приведены примеры, что значительно облегчает понимание темы.