
- •Федеральное государственное бюджетное
- •Глава 1 посвящена изучению общих вопросов теории уравнений (1) с точки зрения известных свойств операторов.
- •§2. Исследование поведения решений однородного уравнения на бесконечности
- •§3. Ограниченность решений однородного уравнения
- •§4.Условия существования ограниченного решения у неоднородного уравнения
- •Глава 2. Численные методы приближенного решения задачи Коши для однородных дифференциальных уравнений в банаховом пространстве
- •§5. Общие сведения о дифференциальных уравнениях
- •§6. Численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка
- •§ 7.Метод Эйлера
- •Решение.
- •§8.Метод Эйлера-Коши
- •Решение.
- •§ 9. Метод Рунге-Кутта
- •Решение.
- •Реализация метода Рунге-Кутта с помощью системы Maxima
- •§10. Решение краевых задач для линейных дифференциальных уравнений второго порядка методом конечных разностей
- •Решение.
- •Реализация конечно-разностного метода
- •§ 11. Метод сеток для решения дифференциальных уравнений в частных производных
- •Решение.
- •Решение.
- •Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima
- •Заключение
- •Список литературы
Решение.
Возьмем
шаг
 Используя расчетную формулу Эйлера-Коши
Используя расчетную формулу Эйлера-Коши найдем приближенное решение задачи
Коши:
найдем приближенное решение задачи
Коши:

 =1.5+0.31=1.81
=1.5+0.31=1.81

 1.81+0.2
1.81+0.2 =1.81+0.3342=2.1442
=1.81+0.3342=2.1442


 =2.1442+0.363724=2.507924
=2.1442+0.363724=2.507924
Таким образом, получили численное решение задачи Коши:
|
|
0 |
0.2 |
0.4 |
0.6 |
|
|
1.5 |
1.81 |
2.1442 |
2.507924 |
Графиком
приближенного решения является ломанная,
последовательно соединяющая точки

Как видим, решения задачи Коши, полученные методом Эйлера и методом Эйлера-Коши очень близки.
Реализация метода Эйлера-Коши с помощью системы Maxima.
Для решения задачи методом Эйлера сформируем еще три пустых
массива
 и вспомогательный массив
и вспомогательный массив

Зададим начальное условие:
![]()
Заполним массив x 2 значениями, начиная с 0.2 до 1 с шагом h .
Для этого используем цикл с параметром.
![]()
Теперь воспользуемся расчетной формулой Эйлера-Коши и найдем решение:

Выведем найденное решение на экран:

Выполним построение найденного решения задачи (4.1) средствами
пакета draw:
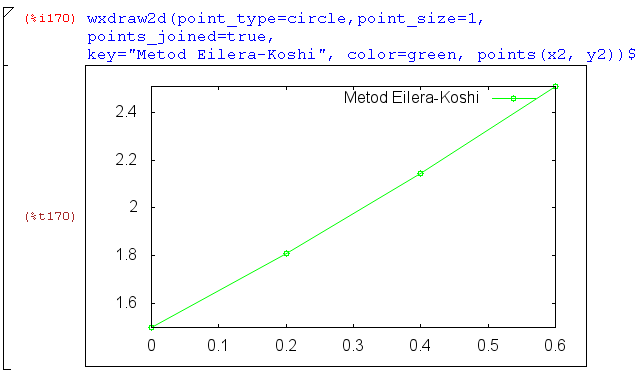
Найдем величину абсолютной погрешности:

Как видим, метод Эйлера-Коши дает более точный результат, чем метод Эйлера. Максимальная погрешность вычислений составляет 0.7%.
§ 9. Метод Рунге-Кутта
Для
простоты записи вместо
 ,
,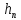 будем писать
будем писать ,
, h.
Пусть r≥2 – целое положительно число и
h.
Пусть r≥2 – целое положительно число и - положительные числа.
- положительные числа.
Пусть
числа
 (s
= 1, 2, . . . ,r-1; m=1, 2, . . . ,s),
(s
= 1, 2, . . . ,r-1; m=1, 2, . . . ,s), удовлетворяют условиям
удовлетворяют условиям
 s
= 1, 2, . . . ,r
s
= 1, 2, . . . ,r 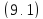

Один
этап метода Рунге-Кутта (переход от
 к
к )
таков.
)
таков.
1).Вычисляются
одно за другим следующие
 чисел:
чисел:
 ,
,

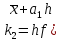 ,
,
 ,
,
 ,
,
 ,
…
,
…
 ,
,
 ,…
,…
 ,
,
 .
.
2). Вычисляется сумма произведений

3).
Вычисляется
 по формуле
по формуле

Числа
 ,
, ,
, при заданномr выбираются так, чтобы
разность
при заданномr выбираются так, чтобы
разность

рассматриваемая
как функция переменного
 была бесконечно малой возможно более
высокого порядкаl
относительно
была бесконечно малой возможно более
высокого порядкаl
относительно
 при
при 0.
Вообще говоря, этим требованиям числа
0.
Вообще говоря, этим требованиям числа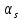 ,
, ,
, не определяются однозначно и при выборе
этих чисел принимаются во внимание
также соображения о простоте формул
не определяются однозначно и при выборе
этих чисел принимаются во внимание
также соображения о простоте формул
Приведем примеры некоторых систем таких чисел и отвечающих им значений l:
 r=2,
r=2,
 ,
, =
= ,
l=3;
,
l=3;
 r=2,
r=2,
 ,
, =1,
l=3;
=1,
l=3;
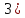 r=3,
r=3,
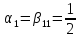 ,
,
,
, ,
, =
= ,
l=4;
,
l=4;
 r=3,
r=3,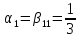 ,
, ,
, ,
, =0,
=0, ,l=4
,l=4
 r=4,
r=4, ,
, ,
,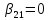 ,
, =
= ,
, ,
l=5;
,
l=5;
 r=4,
r=4, ,
, =
=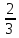 ,
, ,
, ,
,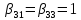 ,
, ,
, =
= ,
, ,
l=5;
,
l=5;
 r=6,
r=6, ,
, =
= ,
, ,
, ,
, ,
, =
= ,
, ,
,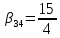 ,
,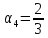 ,
, =
= ,
, =
=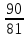 ,
, =
= ,
, =
= ,
,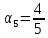 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
,
, ,
, ,
, ,
,
Наиболее
употребительной является система чисел
 .Соответствующий
прием будем называетсяосновным
приемом Рунге-Кутта.
Приведем порядок вычислений в этом
случае.
.Соответствующий
прием будем называетсяосновным
приемом Рунге-Кутта.
Приведем порядок вычислений в этом
случае.
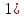 Вычисляется
Вычисляется
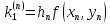 .
.
 Вычисляется
Вычисляется
 .
.
 Вычисляется
Вычисляется
 .
.
 Вычисляется
Вычисляется
 .
.
 Вычисляется
Вычисляется
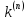 =
= (
( .
.
 Вычисляется
Вычисляется
 .
.
Отметим
также случай ,который
называют иногда усовершенствованным
методом Эйлера; здесь вычисления ведутся
так:
,который
называют иногда усовершенствованным
методом Эйлера; здесь вычисления ведутся
так:
 ;
;
 =
= .
.
3)
В заключении укажем на схему вычислений по методу Эйлера и Рунге-Кутта при решении задачи Коши для системы дифференциальных уравнений первого порядка. Для простоты записи ограничимся случаем системы двух уравнений.
Пусть

Система,
для которой требуется найти решение
 удовлетворяющую условию
удовлетворяющую условию
y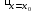 =
= ,z
,z =
=
 Метод
Эйлера. Вычисления проводятся по
формулам:
Метод
Эйлера. Вычисления проводятся по
формулам:

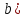 Основной
прием Рунге-Кутта. Вычисления проводятся
по формулам:
Основной
прием Рунге-Кутта. Вычисления проводятся
по формулам:
 ,
,
 ;
;



 ;
;

 ;
;
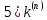 =
=
 (
( ,
,
 =
=
 (
(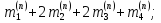

Пример
9.1. Применяя
метод Рунге-Кутта найти решение задачи
Коши
 в
трех последовательных точках
в
трех последовательных точках ,
, ,
, .
.


