Глава 1 посвящена изучению общих вопросов теории уравнений (1) с точки зрения известных свойств операторов.

В §1 выводятся формулы, позволяющие выразить решение однородного и неоднородного уравнений через операторную экспоненту . Рассматриваются некоторые линейные уравнения в пространстве операторов.

В §2 изучается поведение решений однородного уравнения на бесконечности в связи с характером расположения спектра , выясняется геометрический смысл рассматриваемых фактов.

В §3 исследуются условия ограниченности на всей действительной оси решений однородного уравнения. Здесь рассматривается и уравнение второго порядка с оператором, действующим в прямой сумме двух банаховых пространств.

§4 посвящен изучению неоднородного уравнения. Здесь вводится важное понятие функции Грина и с помощью этой функции рассматривается ряд задач, касающихся условий существования ограниченных на всей оси и на полуоси решений.

Глава 2 посвящена изучению численных методов,с помощью которых осуществляется решение задачи Коши для уравнения (1).

§5 посвящен общим сведениям о дифференциальных уравнениях, рассматриваются некоторые определения и теоремы.

В §6 рассматривается постановка задачи Коши для системы обыкновенных дифференциальных уравнений (1), изучается формула погрешности для характеристики точности численного метода, рассмотрены некоторые определения.

В §7 исследуется метод Эйлера, выясняется геометрическая интерпретация данного метода, приведены примеры решения и реализация метода в математическом пакете.

§8посвящен изучению метода Эйлера-Коши, здесь рассматривается отличительная особенность метода Эйлера-Коши от метода Эйлера, выясняется геометрическая интерпретация данного метода, приведены примеры решения и реализация данного метода решения в математическом пакете.

В §9 исследуется метод Рунге-Кутта, выводятся соответствующие формулы, рассматривается такое понятие, как основной прием Рунге-Кутта, приведены примеры и реализация данного метода в системе компьютерной математики Maxima.

§10 рассматривает решение краевых задач для уравнений второго порядка методом конечных разностей, приведены соответствующие примеры.

§11посвящен методу сеток для решения дифференциальных уравнений в частных производных, рассматриваются важные определения, приведены примеры.

В работе принята единая нумерация параграфов. Нумерация формул своя в пределах каждого параграфа. Формулы имеют двойную нумерацию: например, (2.1) означает, что речь идет о формуле 1 из §2.

Основные результаты ВКР докладывались на заседаниях кафедры математического анализа и элементарной математики, на заседаниях НСО, на научно-практической конференции преподавателей и студентов физико-математического факультета 9 апреля 2014 года.

ГЛАВА 1. Линейные дифференциальные уравнения первого и второго порядка с постоянным оператором в банаховом пространстве.

§1. Решение однородного и неоднородного уравнений в векторной и операторной формах.

Рассмотрим дифференциальное уравнение

в банаховом пространстве с постоянным оператороми непрерывной вектор-функцией.

Определение 1.1 Банаховым пространством называется полное нормированное векторное пространство.

Пространство будем называтьфазовым пространством уравнения.

Обратимся к однородному уравнению

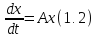
Решение задачи Коши для уравнения с условием

получено в [12] с использованием оператор - функции .

Вектор-функция

имеет непрерывную производную и является решением задачи . Это решение является единственным в классе дифференцируемых функций. Достаточно показать, что если непрерывная функция, удовлетворяющая уравнению, обращается в нуль в точке, то она обращается в нуль и в некоторой её окрестности[12].

Такая функция должна удовлетворять уравнению

Откуда следует при оценка

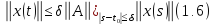
приводящая при к противоречию, если

Применяя метод вариации постоянной, можем найти решение задачи Коши для неоднородного уравнения в виде

После такой замены уравнение примет вид

Откуда

и наконец

Очевидно, что выражение представляет собой дифференцируемую функцию. Кроме того, решениезадачи Кошиединственно, поскольку единственно решение задачи Коши для однородного уравнения.

Приведём решение этой задачи в операторной форме. Предположим, дан оператор , где, удовлетворяет уравнению

и условию .

Рассмотрим более общее операторное уравнение

в фазовом пространстве . Перепишем уравнениев виде [6]

Поскольку операторыикоммутируют, решение уравнения, удовлетворяющее условию имеет вид

Точно так же можно получить для решения уравнения

где - непрерывная функция со значениями из формулу