конспекты по молякулярной физике

универсальной, т.е. выражаться формулой S=S(w) одной и той же для всех систем. Вид этой функции можно установить, пользуясь общими свойствами энтропии и вероятности. Энтропия аддитивна, вероятность мультипликативна.

Рассмотрим две независимые подсистемы с вероятностями состояния w1 и w2 и энтропиями S(w1) и S(w2). Объединим их в одну систему и обозначим вероятность её состояния w. Согласно термодинамике энтропия сложной системы должна быть равна сумме энтропий составляющих её подсистем. Вероятность произведения (одновременной реализации) независимых событий должна равняться произведению вероятностей.

Чтобы из этой системы найти вид функции S(w), наложим условие w = const.

Тогда S(w1) + S(w2) = const

W1--W2 = const

Дифференцируя, получим:

При выводе этого соотношения предполагалось, что аргументы w1 и w2

связаны условием w1-w2 = const. Однако значения этой постоянной, а с ней и аргументов w1 и w2 могут быть какими угодно. Значит, в предыдущем соотношении w1 и w2 могут независимо принимать любые значения. Но слева стоит функция только w1, а справа - только w2. Равенство между ними возможно тогда и только тогда, когда выражения S'(w1)-w1 и S'(w2)-w2 равны одной и той же постоянной. Обозначив эту постоянную буквой k, получим

dS w— = к,

dw

dS = kdw, w

S = k ln w + C .

Постоянная интегрирования С должна равняться нулю. Чтобы доказать это, подставим найденное решение в исходное уравнение (34.1).

k ln(w w ) + C = k ln w + C + k ln w + C , откуда следует С = 0.

Таким образом, S =klnw.

Чтобы определить численное значение постоянной k, достаточно найти независимыми способами, а затем сравнить разность энтропий какой-либо системы в двух произвольных состояниях и логарифм отношения вероятностей тех же состояний. Проще всего использовать идеальный газ. Как было показано в термодинамике (13.10), изменение энтропии S2 - S1 одного моля идеального газа при изотермическом расширении от объёма V1 до объёма V2 равно

Для нахождения отношения вероятностей этих состояний рассмотрим моль газа (число молекул - число Авогадро), находящийся в сосуде объёмом V0. Пусть V - объём какой-либо части этого сосуда. Вероятность того, что какаято молекула попадёт в объём V равна V/V0, а вероятность того, что в объёме V окажутся все N =NA молекул, равна (V/ V0)N. Тогда отношение вероятностей

Из этого соотношения находим

k=-R,

Na

т.е. k - это постоянная Больцмана.

Фундаментальное соотношение между энтропией и вероятностью было установлено Больцманом и называется формулой Больцмана:

Соотношение (34.3), на первый взгляд, может показаться противоречащим термодинамике. Если рассматривать w как математическую вероятность (w <

1), то из (34.3) следует S < 0. Это противоречие устраняется тем, что в термодинамике вероятности не обязательно определять однозначно. Однозначно должны определяться не сами вероятности, а их отношения в различных состояниях. Планком была введена в рассмотрение

термодинамическая вероятность, в которой вероятности выражаются целыми положительными числами. Макросостояние - это состояние системы, характеризуемое её термодинамическими параметрами. Состояние же системы, характеризуемое состоянием каждой входящей в систему молекулы, называют микросостоянием. Так как молекулы движутся

хаотически, то имеется много микросостояний, соответствующих одному макросостоянию. Обозначим Г - число микросостояний, соответствующее данному макросостоянию (как правило, Г >>1).

Термодинамической вероятностью или статистическим весом макросостояния Г - называется число микросостояний, осуществляющих данное макросостояние.

Тогда формулу Больцмана можно записать так:

S = k ln Г

§35. Флуктуации.

Если рассмотреть сосуд с газом, содержащий N молекул, и поставить вопрос, сколько молекул содержится в одной из половин сосуда, то ответом будет «примерно N/2». Из-за хаотического теплового движения число молекул будет отклоняться от среднего значения N/2, флуктуировать.

Флуктуация -это случайное отклонение какой-либо величины F от её среДнего значения<Г >.

где AF - флуктуация. Среднее значение флуктуации равно нулю ((AF) = 0),

поэтому оно не годится в качестве меры флуктуаций. Чтобы охарактеризовать величину отклонений физической величины, используют

Дисперсию DP = ((AF)2^ или среДнее кваДратичное отклонение <3P=JD.

Среднее квадратичное отклонение qf удобнее для характеристики флуктуаций, чем дисперсия DF , так как имеет такую же размерность, как F.

Дисперсию можно представить в следующем виде:

(AF2) = {(F- (F)2) = {F2 -2F{F)+ (F)2) = {F2)-{F)2.

При этом учитывалось, что <F> - величина постоянная, а поэтому

Отношение среднего квадратичного отклонения к среднему значению флуктуирующей величины называется среДнекваДратичной относительной флуктуацией.

°F

3F И

Рассмотрим физическую систему, состоящую из N одинаковых независимых частей. Примером такой системы может служить идеальный газ, а составных частей - отдельные молекулы. Пустьfi некоторая аддитивная величина, характеризующая i-ю составную часть, например кинетическая энергия поступательного движения i-й молекулы (f==mv?/2), а F - сумма

кинетических энергий поступательного движения всех молекул системы. Значения fi и F флуктуируют.

F = Xf

i=1

Так как составные части одинаковы, то средние значения f у них равны

друг другу ii) = (j = {f).

N

F = Z(f) = Nf

i=1

NN

F1 =Y f2 +Zff

i=1 hj

Так как составные части независимы друг от друга, ff^ = Ц) ={f)г•

{f2) = N{f2) + N(N -1) (f2 = N[f2) + N2 (f2 -Nf2

F2 = N2{f)2

a2f =<f2) -f2

Среднеквадратичная относительная флуктуация величины f обычно порядка единицы.

В нашем случае (f2) = (m2v4 / 4^ = 15k2T2 / 4 .

af = y/(m2v4 /4 -(mv' 2Y = V15k2T2/4 - 9k 2T 2/4 = кЛ/зТ2

3F

(F) Nf 4N

Таким образом, относительная флуктуация величины F убывает обратно пропорционально квадратному корню из числа элементов, поэтому в системе, состоящей из очень большого числа элементов, она очень мала.

Рассмотрим ещё один пример. В сосуде объёмом V содержится N молекул. Выделим мысленно объём v. Среднее число молекул в выделенном

объёме „ =N—. Найдём среднеквадратичную флуктуацию числа n

молекул в выделенном объёме. Введём в рассмотрение функцию fi, которая равна 1, если i-ая молекула находится в объёме v и равна 0, если i-ая молекула находится в объёме V-v. Эта функция интересна тем, что её возможные значения и их квадраты совпадают.

N

флуктуация

§36. Реальные газы. Уравнение Ван-дер-Ваальса. Внутренняя энергия газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение газов при низких давлениях и не очень низких и не очень высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные - не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса - это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием.

Рассмотрим сначала моль газа, в котором частицы не взаимодействуют друг с другом и имеют пренебрежимо малые размеры. Такой газ удовлетворяет уравнению состояния идеального газа:

RT

(36.1)

Учтём размер частиц, Предположим, что частицы данного газа являются шариками одинакового радиуса r . Так как газ находится в сосуде конечного объёма, то пространство, доступное для перемещения частиц, будет несколько меньше V. В формуле (36.1) следует вычесть из всего объёма некую его часть b, зависящую от вещества, из которого состоит газ. Таким образом, вводится поправка, учитывающая конечный размер молекул или силы отталкивания между ними.

Стоит заметить, что вычитаемый объём b не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми шариками, то вычитаемый объём будет примерно в четыре раза больше. Это объясняется тем, что центры шаров не могут сближаться на расстояние меньшее 2r . Учёт сил отталкивания молекул приводит к некоторому увеличению давления реальных газов по сравнению с идеальными.

Силы притяжения между молекулами газа несколько уменьшают давление. Мысленно наметим поверхность, разделяющую сосуд с газом, и рассмотрим взаимодействие газа через неё. При хаотическом тепловом движении молекулы будут осуществлять перенос импульса через поверхность, что приводит к отталкиванию (см. вывод основного уравнения МКТ идеального газа (26.2)). Сила притяжения, действующая на одну молекулу вблизи поверхности со стороны молекул, находящихся с другой стороны, пропорциональна концентрации n, и число таких притягиваемых молекул пропорционально n. Таким образом, поправка к давлению, обусловленная притяжением молекул, пропорциональна n2, или обратно пропорциональна квадрату объёма:

21

\p ~ n---- -. V2

По знаку эта поправка отрицательна. Объединяя поправки, получим уравнение Ван-дер-Ваальса для одного моля газа:

Значения параметров а и b зависят от газа. Уравнение Ван-дер-Ваальса неплохо работает при b«V, a C«p. Если эти условия не выполняются, то в количественном отношении расчёты отклоняются от эксперимента, но качественное согласие остаётся.

Обычно уравнение Ван-дер-Ваальса для одного моля газа записывают в виде:

Такая форма записи является традиционной, но в расчётах удобнее использовать (36.3).

Легко получить уравнение Ван-дер-Ваальса для v молей. Для этого вместо V в уравнении (36.4) надо написать V/v:

Для нахождения внутренней энергии моля газа Ван-дер-Ваальса применим термодинамические функции (§16-§17, соотношение (17.2)):

'дU ' =T 'др_л -P.

Дифференцируя (36.3), получим:

'dU_г R RT a

^дУ )т ~ У - b У - b У2 ’

'dU л a

<дУ ,т У2 ’

Интегрируем по объёму, считая температуру постоянной

где Const = ^(Т) не зависит от объема газа, но зависит от температуры.

Используем теплоёмкость CV

"dU л

X = Cv =(d^/dT)v,

dT = CvdT,

Здесь Const не зависит от температуры, но зависит от объема.

идеальных газов, температура реальных газов при этом понижается.

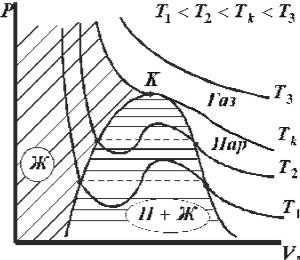
§37. Изотермы реального газа. Критическая точка.

Для исследования особенностей поведения реального газа, рассмотрим изотермы газа Ван-дер-Ваальса. Построим кривые зависимости давленияP от объёма V при разных температурах T , используя уравнение Ван-дер- Ваальса для 1 моля газа (36.3). На рис. 37.1 приведены эти кривые для четырёх различных температур Т1< Т2< Тк< Т4. При высоких температурах T > Тк изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре T на изотерме имеется точка перегиба

K . Эта изотерма называется критической, соответствующая ей температура Тк - критической температурой, а точка K - критической точкой. Состояние

с критическими параметрами называется критическим состоянием.

Рис. 37.1 Изотермы реального газа на pV - диаграмме.

При температурах Т < Тк изотермы, построенные по уравнению (36.3),

уменьшается, а при увеличении возрастает. Система с такими свойствами была бы неустойчивой. Поэтому у реальных изотерм такого волнообразного участка нет. Вместо этого, если Т< Т, при сжатии газа с некоторого момента давление перестаёт возрастать, а на стенках цилиндра появляются капли жидкости. По мере уменьшения объёма количество жидкости возрастает, пока весь газ не превратится в жидкость. На рис. 37.1 этому соответствует прямолинейный изобарический участок, изображённый пунктиром. Если через крайние точки горизонтальных участков семейства