конспекты по молякулярной физике

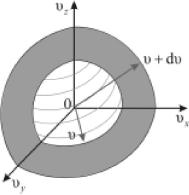
§30. Распределение молекул по абсолютным значениям скорости. Ха­ рактерные скорости молекул.

В данном параграфе нас будет интересовать распределение абсолют­ ных значений (модулей) v скоростей молекул (v = v2 + v2 + v\ ). Число моле­

кул dN , имеющих модули скорости v в узком интервале от v до v + dv, про­ порционально N, пропорционально ширине интервала dv и зависит от v.

Здесь F(v) - функция распределения модулей скорости.

В пространстве скоростей скоростные точки молекул у которых моду­ ли скорости лежат в узком интервале (v, v+dv) находятся в шаровом слое толщиной dv и радиусом v (рис. 30.1). Объём такого слоя 4nv2dv.

Рис. 30.1.

Кол-во скоростных точек молекул в этом шаровом слое можно выразить с помощью функции распределения молекул по скоростям f(v) (29.3):

dN = N-flv)- l~v\lv. (30.2)

Сравнивая (30.2) и (30.1) найдём: F(v) =flv)-4nv2. Подставляя (29.3) получим

3

F(v) =( m \xp(- m^) -4^v2. (30.3)

Данный закон распределения тоже подчиняется условию нормировки:

Средняя квадратичная скорость:

§31. Столкновения молекул со стенкой сосуда.

Молекулы газа, заключенного в сосуде, сталкиваются при своем дви­ жении с его стенками. Вычислим среднее число z ударов молекул газа об единицу поверхности стенки за единицу времени. Рассмотрим вначале про­ стой случай, в котором молекулы подходят к стенке параллельным пучком, с одинаковыми по величине и по направлению скоростями. Число Z ударов молекул о площадку площади S за время At равно Z = Пп-S v At cos0, где Пп концентрация молекул в пучке, v скорость молекул, 0 угол между направле­ нием скорости и нормалью к стенке. Число молекул пучка, ударяющихся о единицу площади в единицу времени:

Молекулы в сосуде имеют разные по величине и направлению скоро­ сти. Обозначим концентрацию молекул в сосуде n. Чтобы воспользоваться формулой (31.1), выделим молекулы, у которых модули скоростей лежат в узком интервале (v, v+dv). Концентрация этих молекул

dnv = n-F(v) dv.

Их скоростные точки в пространстве скоростей находятся в шаровом слое толщиной dv и радиусом v (рис. 30.1). Концентрацию молекул dnv,e, у которых направления скоростей составляют с нормалью к стенке углы в ин­ тервале (0, 0 + d0), а абсолютные значения скоростей в попадают в интервал (v, v+dv), можно найти следующим образом. Выделим в пространстве скоро­ стей два прямых круговых конуса, общая ось которых совпадает с нормалью к стенке, образующие конусов составляют с осью углы 0 и 0 + d(),n вершина находится в начале координат. Конусы вырежут из шарового слоя область в виде кольца. Отношение площади этого кольца 2лvsm0•vd0•к площади шаро­ вого слоя 4nv2 равно доле молекул, направления скоростей которых состав­ ляют с нормалью к стенке углы в интервале (0, 0 + d0). Тогда

Используя соотношение (31.1) найдём число ударов молекул этой группы

При нагревании нити электрическим током с ее поверхности испаря­ лись атомы серебра. Скорости испарившихся атомов соответствовали темпе­ ратуре нити. Покинув нить, атомы двигались по радиальным направлениям. Внутренний цилиндр имел узкую продольную щель, через которую проходил наружу узкий пучок атомов (молекулярный пучок). Чтобы атомы серебра не отклонялись за счет соударений с молекулами воздуха, весь прибор был эва­ куирован. Достигнув поверхности внешнего цилиндра, атомы серебра оседа­ ли на ней, образуя слой в виде узкой вертикальной полоски.

Рис. 32.1 Прибор для проведения опыта Штерна.

Если привести весь прибор во вращение, след, оставляемый молеку­ лярным пучком, сместится по поверхности внешнего цилиндра на некоторую величину Av.

Это произойдет потому, что за время, пока атомы серебра пролетают зазор между цилиндрами, прибор успевает повернуться на некоторый угол в результате против пучка окажется другой участок наружного цилиндра,

смещенный относительно первоначального следа v на величину Av , равную

RA@ (R - радиус внешнего цилиндра). Расстояние Av между первоначаль­

ной и смещенной полосками серебра можно связать с угловой скоростью вращения цилиндров а, геометрией прибора и скоростью атомов v. Обозна­ чив время пролета через At можно написать, что

Поскольку радиус внутреннего цилиндра (нити) мал по сравнению с радиу­ сом внешнего цилиндра R, время пролета At можно считать равным:

At = R v

Подставив это выражение в (32.2) и разрешив получившееся уравнение относительно v , получим

v = oR1

As

Измерив, смещение следа As и скорость вращения прибора, можно определить скорость атомов v . Положение, правда, осложняется тем, что вследствие распределения по скоростям атомы имеют различные скорости, и в результате смещенный слой будет размытым. Исследуя профиль следа, можно было составить примерное представление о распределении атомов се­ ребра по скоростям.

Результаты опыта Штерна подтвердили правильность оценки средней скорости атомов, которая вытекает из распределения Максвелла. О характере самого распределения этот опыт мог дать лишь весьма приблизительные све­ дения.

Рис. 32.3 Принцип работы опыта Ламмерта.

Более точно закон распределения был проверен в опыте Ламмерта (1929г.), в котором молекулярный пучок пропускался через два вращающих­ ся диска с радиальными щелями, смещенными друг относительно друга на некоторый угол ф (рис. 32.3). Из числа молекул, пролетевших через щель в первом диске, пролетят через второй диск только те, которые подлетят к нему в тот момент, когда на пути пучка встанет прорезь во втором диске. Бо­ лее быстрые молекулы, достигнут второго диска слишком рано, а более мед­ ленные - слишком поздно для того, чтобы пройти через щель.

Таким образом, это устройство позволяет выделить из пучка молекулы, обладающие определенным значением скорости (из-за конечной ширины

щелей прибор выделяет молекулы, скорости которых лежат в пределах неко­ торого интервала Av). Средняя скорость выделяемых прибором молекул мо­ жет быть найдена из условия, что время t , за которое молекулы пролетают

расстояние I между дисками (= l[v) должно совпадать со временем t2, за которое диски повернутся на угол (р (t2 = ^а). Приравняв оба времени, по­ лучим:

v = ®7/ф.

Меняя скорость вращения прибора о (или угол между дисками ф),

можно выделять из пучка молекулы, обладающие различными значениями скорости. Улавливая затем эти молекулы в течение определенного времени, можно определить их относительное количество в пучке.

Результаты опыта Ламмерта и других опытов, предпринимавшихся с той же целью, находятся в полном согласии с законом распределения, уста­ новленным теоретически Максвеллом.

Следует отметить, что распределение молекул по скоростям в пучке, вышедшем через отверстие в сосуде, несколько отличается от распределения, имеющегося в сосуде. Так как более быстрые молекулы будут проходить че­ рез отверстие в относительно большем количестве, чем более медленные, пу­ чок будет обогащен более быстрыми молекулами. Поскольку количество мо­ лекул, пролетающих через отверстие в единицу времени, пропорционально v , распределение в пучке будет характеризоваться функцией

F(у) = Ae~-2kTvi

где A - нормировочный множитель. Наиболее вероятная скорость в этом случае равна v = ^J3kT/m , а средняя скорость У = ^/9лкТ/8m .

§33. Распределение Больцмана.

Если идеальный газ находится в силовом поле, то концентрация молекул не может быть одинаковой во всех точках. Это следует из условий механического равновесия. Пусть идеальный газ находится в однородном (g = const) поле тяжести (рис. 33.1). Температура газа Т во всех точках одинакова. Выделим вертикальный цилиндр, площадь основания которого равна S, и рассмотрим слой газа малой толщины dh на высоте h. Сила тяжести, действующая на этот слой равна m-g-n(h)-S-dh, где n(h) концентрация молекул на высоте h, m масса молекулы. Сила тяжести уравновешена силами давления:

(P - (P + dP))-S = m ■g-n(h)-S-dh

Учитывая, что P = nkT, это соотношение можно переписать в виде:

Если от концентраций вернуться к давлениям, получим барометрическую

Формула (33.1) выражает распределение Больцмана для молекул идеального газа в однородном поле тяжести. Потенциальная энергия молекулы mgh, n0 концентрация газа там, где потенциальная энергия молекул равна нулю. Можно связать n0 с полным числом молекул в сосуде N. Для этого надо знать

форму сосуда. Самый простой случай, если сосуд - вертикальный цилиндр с площадью основания S и высотой Н. Число молекул в слое толщиной dh на высоте Н

dN = n(h) S dh.

mgN

n0

kTS(1 - exp(- nmgH)). kT

Можно было бы не интегрировать, а использовать барометрическую формулу (33.2) и условия равновесия

mgN = Po S - P(H)S = kTn,(1 - exp(- mgH))s .

При более сложной форме сосуда, связь n0 и N тоже усложнится.

В формуле распределения Больцмана молекул идеального газа в поле тяжести (33.1) можно вместо отношения m/k использовать ц/R.

Если рассматривать распределение молекул газа в любом потенциальном силовом поле, где потенциальная энергия молекулы в точке r равна s( r), то можно показать, что распределение молекул будет выражаться соотношением, аналогичным (33.1)

Это распределение Больцмана в общем виде.

Потенциальных силовых полей, в которых могут находиться молекулы идеальных газов, не так уж много. Например, во вращающейся вокруг неподвижной оси с угловой скоростью ® неинерциальной системе отсчёта поле центробежных сил инерции потенциально. Как известно из механики,

потенциальная энергия молекулы, находящейся на расстоянии r от оси в этом

§34. Статистический смысл энтропии.

Вспомним закон возрастания энтропии: энтропия адиабатически изолированной системы не может убывать. При обратимых процессах она остается неизменной, при необратимых процессах возрастает. Рассмотрим простейший необратимый процесс с точки зрения молекулярно­ кинетической теории. Сосуд разделён перегородкой на две равные части Iи II. В части 1находится N молекул идеального газа, а в части II- ни одной.

Перегородку мгновенно убирают. Молекулы из части I будут переходить в часть II. Спустя некоторое время возникнет и обратный поток. Будет происходить обмен молекулами между частями сосуда. Может показаться, что в результате такого обмена все N молекул могут вернуться в часть I и процесс окажется обратимым. Однако при N >> 1 такие процессы никогда не наблюдаются. Проведём расчёт вероятности обратного процесса в зависимости от N. Если N=1, то никакой необратимости нет. В отсутствии внешних силовых полей, молекула с равной вероятностью может попасть как в часть I, так и в часть II. Вероятность найти молекулу в части Iравна 1/2. Если N=2, то попадания их в одну или другую часть будут независимыми событиями (газ идеальный). Вероятность того, что они обе окажутся в части

I, найдётся по теореме умножения вероятностей, и будет равна

(1/2)-(1/2)=1/4. Если в сосуде N молекул, то вероятность w попадания их всех в часть I будет равна w=(1/2)N . При N=10 w=(1/2)10=1/1024«10-3. В этом случае обратный процесс не часто, но может реализоваться. Однако при N=100 w=(1/2)100«1O-30, и нет никаких шансов наблюдать обратный процесс. Отметим, что системы из 100 частиц далеко не макроскопические. Если N = 1020, то вероятность w настолько мала, что с ней можно совершенно не считаться. Таким образом, необратимость термодинамических процессов связана с тем, что обратные процессы крайне маловероятны. С другой стороны, согласно термодинамике, все самопроизвольные процессы в замкнутых системах сопровождаются возрастанием энтропии. Поэтому можно ожидать, что между энтропией системы S в каждом состоянии и вероятностью w того же состояния должна существовать однозначная связь. Данная гипотеза была выдвинуга Больцманом. Эта связь должна быть