
конспекты по молякулярной физике
.pdf
|
T - T |
|
|
C.dT. = -kS |
—----T- dt, |
|
|
1 |
1 |
l |
(25.3) |
|
- |
- - |
|
|
|
||
CdT = kSt--- 2- dt. |
|
||
2 |
2 |
l |
|
Обозначим буквой 0 разность температур тел |
0 =- -- . |
||
Тогда |
|
d0 = d- - d- . |
|
Разделим первое уравнение (25.3) на С1, а второе на С2, и вычтем вто рое из первого. Получим
|
( 1 |
1 |
|
к . |
|
|
d0=-_ |
i |
|
A |
, |
(25.4) |
|
---- 1---- |
• 0 • dt. |
|
||||
l |
C1 |
C2 |
|
J ....... |
|
|
|
■ |
|
|
|
|
|
Введем обозначение |
1_ kS r |
i |
i ' |
|
||
T |
l |
|
|
|
|
|
|
|
|
|
|
||
Постоянная T имеет размерность времени. Тогда уравнение (25.4) мож но записать в виде
d0 _ |
dt |
|
0 |
T |
|
Интегрируя, получим |
|
|
0(t)=T1(t)-T2(t)= 00 • e-t / T, |
(25.5) |
|
где 0 =T -T начальная разность температур.
Заметим, что из соотношения (25.2) следует
C1T1 + C2T2 = const = C1T10 + C2T20.
Решая систему уравнений (25.5-6), можно найти зависимости
T2(t)
T1 (t)= |
C1T10 |
+ C2T20 |
+ |
C2 |
T |
|
C1 |
+ C2 |
1 |
(t10 - T20 )• e~t/ |
|||
|
|
|
+C2T20 |
|
C + C2 |
— - T20 )• e T |
2 |
(t)= |
C1T10 |
----- C |
|||
T |
C1 + c2 |
|
C1 + c-12 —2 0 |
|||
|
|
|
||||
(25.6)
T1(t) и
(25.7)
Рассмотрим случай, когда теплоёмкость второго тела бесконечно вели ка С2 = да. Тогда его температура будет оставаться постоянной Т2 = Т0.
В этом случае зависимость температуры первого тела от времени
T1(t) =T0 + (T10 -T0) •e-t/T |
(25.8) |
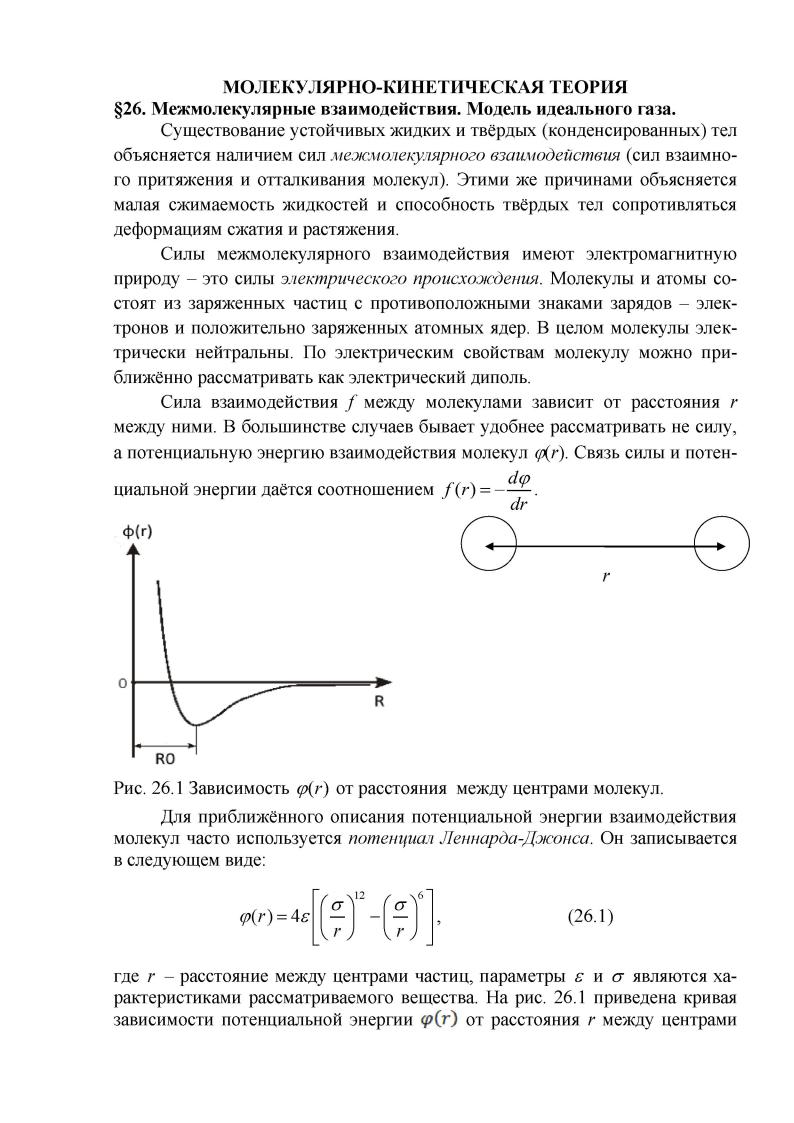


§27. Молекулярно-кинетический смысл температуры. Равномерное рас пределение кинетической энергии по степеням свободы.
Можно показать, что в состоянии теплового равновесия средняя кине-
m(vv)
тическая энергия —-— поступательного движения молекул, подчиняющихся
законам классической механики, имеет одно и то же значение. Поэтому средняя кинетическая энергия молекул обладает основным свойством темпе ратуры - в состоянии теплового равновесия она одинакова для всех молекул газов, находящихся в тепловом контакте, а также для различных молекул га зовой смеси. Поэтому кинетическую энергию можно принять за меру темпе ратуры газа. В этом и состоит физический смысл температуры с молекуляр но-кинетической точки зрения.
Найдём связь между средней кинетической энергией поступательного движения молекулы газа и его температурой. Скомбинируем основное урав нение МКТ с уравнением состояния идеального газа
2 m\v ] |
ТЛ 2 m(v2 |
p = — n—-—pV = —N—-—
3 |
2 |
3 |
2 |
|
pV = vRT |
|
|
|
N = vNA |
|
|
|
2 |
m(v2} |
|
|
pV = 3A |
2 |
|
-mV
RT = - N |
2 |
|
3A |
|
|
- Na m(v2) |
|
|
3 R |
2 |
|
Используя постоянную Больцмана k |
R получим: |
|
|
|
NA |
(27.1)
Молекулы можно рассматривать как системы материальных точек (атомов) совершающих как поступательное, так и вращательное движения. При исследовании движения тела необходимо знать его положение относи тельно выбранной системы координат. Для этого вводится понятие о степе нях свободы тела.



положений равновесия. Энергия этих колебаний и представляет собой внут реннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следова тельно, каждый атом имеет 3 колебательные степени свободы. При гармони ческих колебаниях средняя кинетическая энергия равна средней потенциаль ной энергии. Поэтому в соответствии с теоремой о равномерном распределе нии на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом - 3kT. Внутренняя энергия 1 моля твердого вещества равна:
U = 3NkT = 3RT
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
Cv = 3R = 25,12Дж / моль ■ K
Это соотношение называется законом Дюлонга-Пти. Для твердых тел практически не существует различия между C и C из-за ничтожно малой
работы при расширении или сжатии. Опыт показывает, что у многих твердых тел (химических элементов) молярная теплоемкость при обычных темпера турах действительно близка к 3R рис. (28.2). Однако при низких температу рах наблюдаются значительные расхождения между теорией и эксперимен том. Это показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением. Наблюдаемая на опыте зависи мость теплоемкости от температуры может быть объяснена только на основе квантовых представлений.
Рис. 28.2 Зависимость теплоёмкости меди от температуры.
§29. Распределение молекул по скоростям. Распределение Максвелла.
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновениях изменяется. Она может менять направ ление, возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется опре деленному статистическому закону. Скорость отдельной молекулы с течени ем времени будет меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоро стью. Дело в том, что, число молекул хотя и очень велико, но конечно, а чис ло значений скорости бесконечно (континуум). Ни одна молекула не облада ет точно заданной скоростью.
Введём в рассмотрение пространство скоростей, в котором по осям прямоугольной системы координат отложены компоненты скоростей моле кул. В таком пространстве каждой молекуле соответствует скоростная точ ка vx,vy,vz. Совокупность скоростных точек образует облако в пространстве скоростей. Это облако сферически симметрично. Концентрация точек в об лаке зависит только от расстояния до центра, определяемого модулем скоро сти v (v2 =v2x + v2y + v2x).
Распределение молекул по скоростям можно описать, введя функцию распределения. Рассмотрим вначале функцию распределения компоненты скорости. Пусть в объеме находится N молекул (N >>1). Число молекул dN , имеющих компоненту скорости vx в узком интервале от v до vx + dvx, про порционально N, пропорционально ширине интервала dvx и зависит от vx
dN(vx,Vx+dvx) = N^(vx)dvx,
где vx ) называется функцией распределения компоненты скорости. Она связывает долю молекул, имеющих скорости в этом интервале, с шириной интервала:
dN |
|
N = P(vx )dVx . |
(29.1) |
Доля молекул AN/N, имеющих компоненту скорости в широком интервале |
|
(vx1,vx2) определяется интегралом |
|
Vx2 |
|
= j |
)dvx |
Vx1

Любая функция распределения должна удовлетворять условию нормировки:
+х
j <р(ух)dvx =1
—X
Можно показать, что функция распределения для компоненты скорости v выглядит следующим образом:
(29.2)
Так как все направления равноправны (облако скоростных точек сферически симметрично), функции распределения для двух других компонент ф(гу) и ф(у2) будут иметь такой же вид.
Теперь рассмотрим маленький объем пространства скоростей (рис.29.1). В нём компоненты скоростей молекул попадают в интервалы (vx,vx+dvx), (vy,vy+dvy), (vz,vz+dvz). Число молекул dN, скоростные точки кото рых попадают в этот объём, пропорционально полному числу молекул N и
величине объёма dvxdvydvz. Коэффициент пропорциональности f(v) называ-
ется функцией распределения молекул по скоростям
dN = Nf(v) dvxdvydvz.
Долю молекул, попадающих в этот объ ём, можно найти используя функции распре деления компонент скорости:
dN = ф(к)dVx ф^, yd-Vy Ф(уг )dVz
Рис.29.1.
Это позволяет связать функцию распределения молекул по скоростям f(v) с функциями распределения компонент скорости
f(v) = ^(Vx)^(Vy)^(Vz).
