Periodic electromagnetic field in the conductors. (Периодическое электромагнитное поле в проводниках)

These approaches are very important form of existence of electromagnetic field – electromagnetic wave. That’s the case when the electric field intensity or magnetic field intensity depends on time according to sinusoidal function:

Quasi-stationary approaches:

The electromagnetic field is often called a planner electromagnetic wave. To describe it let’s use the complex method (using to describe currents and voltage in electromagnetic circuits):

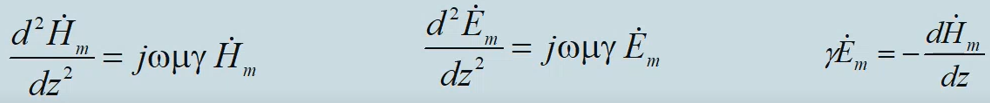
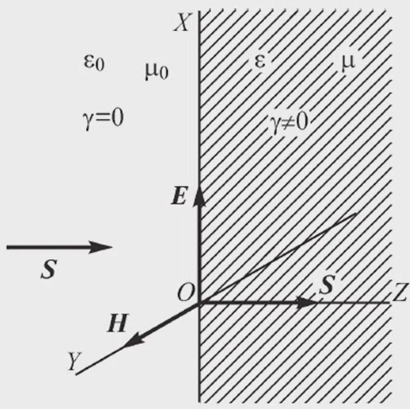
On the picture: in the left part γ is equal to 0, so electromagnetic wave comes from somewhere to this planner surface and then it starts to penetrate the conducting material (metal):

Equation:
Solution for the complex field intensity:
Parameter α:
Using designation:
Solution for the field intensity:

( , because: decreases, when we are travelling into the conducting medium and field intensity is growing to infinity)

Penetration of the electromagnetic field into a conductor. (Проникновение электромагнитного поля в проводник)

Everywhere inside the conductor the magnetic field intensity will be oscillating function, but the amplitude of this oscillation will be less and less:

The penetration length:

Amplitude of the electromagnetic wave dumps according to exponential dependence:

The skin effect. (Скин-эффект)

The maximum value of the amplitude of the electromagnetic field corresponds to the left and right side of the conducting plate. When we move into the center of the conducting plate, the magnetic field decreases, and the amplitude become smaller and smaller. In the center the disappearing is almost completes.

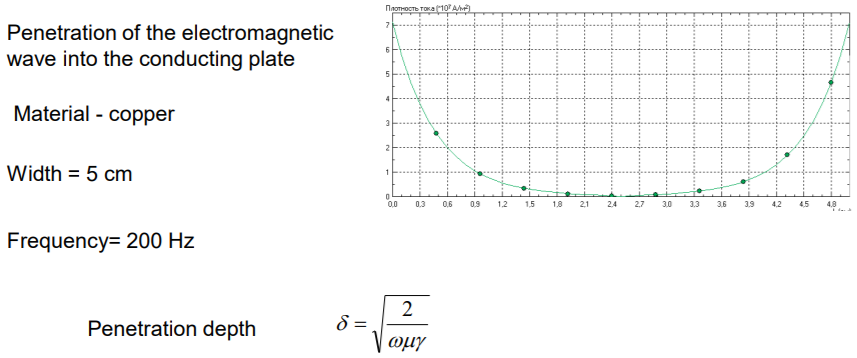
Penetration depth:

Penetration length – it’s the position where the amplitude decreases by the e=2.73

Poynting’s Theorem. (Теорема Пойнтинга) Electromagnetic Field Energy. (Энергия электромагнитного поля)

The energy of the electromagnetic field enclosed inside a certain volume V, bounded by a closed surface S, is determined by the volume energy density of the electric and magnetic fields.

To determine the rate of the energy variation in time dependent electromagnetic field, it is necessary to differentiate the corresponding expression by time:

The rate of decrease of the electromagnetic field energy in a closed volume. (Скорость уменьшения энергии электромагнитного поля в замкнутом объёме)

The main relations between the characteristics of the electromagnetic field:

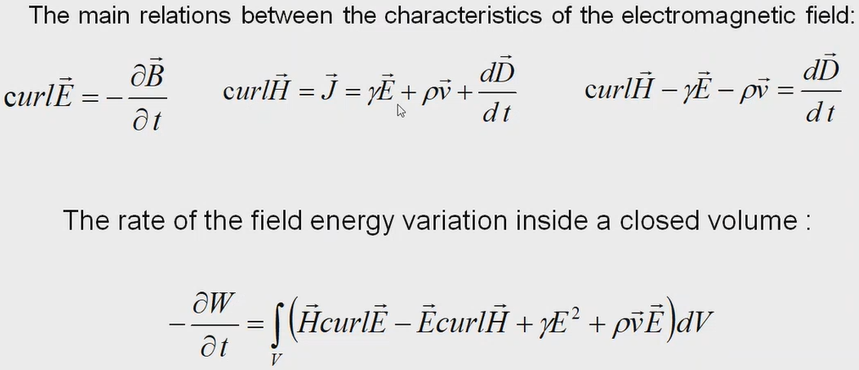
The rate of the field energy variation inside a closed volume:

The volume of divergence of any vector may be replaced by the integral of the closed surface of this volume.

Using the algebra formula , we get:

After applying the Gauss theorem:

The resulting expression is called the Poynting’s theorem.

The first term of this expression corresponds to energy losses for heating the conductor.

The second term is equal to the energy of the electric field spent on the acceleration of charged particles in the volume V.

The third term characterizes the energy of the electromagnetic fields carries across the boundaries of the area.

The power of radiated electromagnetic energy is numerically equal to the flow of energy through the surface per unit of time.

The Poynting vector:

The energy of the electromagnetic field is transmitted if the electric and magnetic intensity vectors are nor parallel.