Advanced chapters of theoretical electro-engineering. Lecture 2
1
Poisson’s and Laplace’ s equations.
E U |
In the absence of free charges D 0 |
|
|
D E |
|
For the linear dielectric const |
U 0 |
|
2 |
|
U 0 |
|
|
|
Laplace’s equation
In general case
For the linear dielectric
U
U
Poisson’s equation
2
Boundary conditions for the Laplace or Poisson Equations
Laplace’s (Poisson’s) equation has unique solution:
1-st type boundary conditions |
U F1 |
|
(Dirichlet boundary conditions) |
U 0 |
|
|
|
2-nd type boundary conditions (Neumann boundary conditions)
U F2n
3-rd type boundary conditions |
U |
U F3 |
|
n |
|
3
Electrostatic Energy.
The force in the electric field |
|
|
F Q E |
|
||||||||||
|
|
b |
|
|
b |
|
|
|
|
b |
|
|
||
The work |
A |
|
dl |
|
|
|
|
|
|
|
|
|||
|
F |
Q E dl |
Q |
E dl |
||||||||||
|
|
a |
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
b |
|
|
|
A |
|
|
|
|
|
The potential difference |
|
|
Ua Ub E |
dl |
|
|
|
|
|
|||||
|
|
Q |
|
|
||||||||||
|
|
|
|
|
a |
|
|
|
|
|
||||
For infinitely remote point a |
|
|
Ua 0 |
|
Ub |
|
A |
|
|
|
||||
|
|
|
Q |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
The work is done by the electric field without any external force |
||||||||||||||
Energy conservation law |
|
|
A W 0 |
|
A W |
|
||||||||
So we have got Wb Q U
4
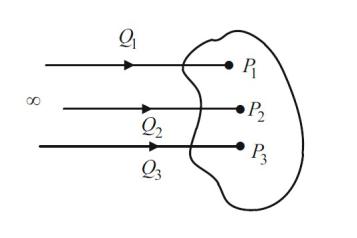
Electrostatic Energy.
Consider three points P1, P2, and P3 in a charge- free space. The point charges Q1,Q2, and Q3 are brought from infinity to those points, respectively.
WE W1 W2 W3
No work is done in bringing point charge Q1 from infinity to point P1
WE 0 W2 W3 or |
WE 0 Q2U21 Q3 U31 U32 |
U21 is the potential at point P2 due to Q1,
U31 is the potential at point P3 due to Q1,
U32 is the potential at point P3 due to Q2.
5
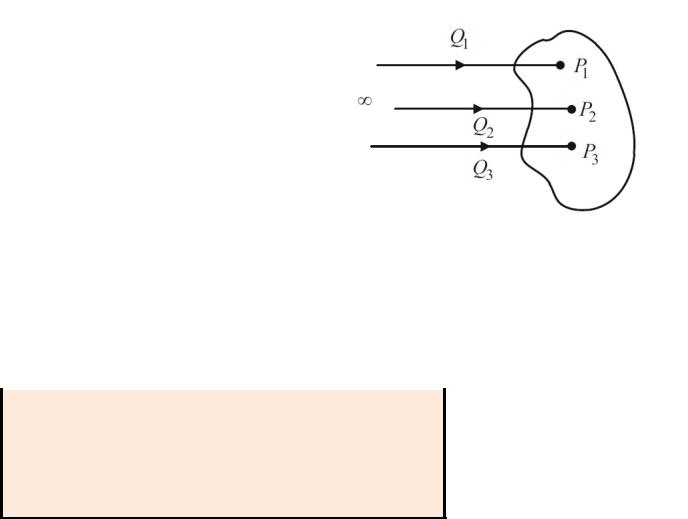
Electrostatic Energy.
Placing the point charges in the reverse order:
WE 0 Q2U23 Q1 U12 U13
Adding the equations we shall get
2WE Q1 U12 U13 Q2 U21 U23 Q3 U31 U32
or |
2WE Q1U1 Q2U2 Q3U3 |
|
|
WE 1 |
Q1U1 Q2U2 Q3U3 |
|
2 |
|
6
Electrostatic Energy.
|
WE 1 |
N |
In general case: |
QnUn |
|
|
2 n 1 |
|
If the charges are distributed over the space
W |
2 V |
|
|
1 |
UdV |
for the space charges |
|
E |
|
|
|
|
2 |
S |
|
WE 1 |
UdS for the surface charges |
||
W |
2 |
l |
|
1 |
Udl |
for the line charges |
|
E |
|
|
|
7
Electrostatic Energy.
Substituting in the expression for the |
|
|
divD |
|||||||||||
energy of charges distributed in the volume: |
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
||
|
W |
2 V |
|
|
W |
|
2 V |
|
|
|
||||
|
|
UdV |
|
DUdV |
||||||||||
|
E |
|
|
|
|
|
|
E |
|
|
|
|
|
|
UD U D D U |
|
U D UD D U |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
WE 1 UD D |
U dV |
|
|
|
|||||||||
|
|
|
2 V |
|
|
|
|
|
|
UD dV UDdS |
||||
Applying the Gauss theorem to the first term: |
|
|
||||||||||||
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
V |
|
|
S |
R |
U |
~ |
|
|
D ~ |
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|||||||
|
R |
|
R2 |
|
|
U D ~ |
|
|
||||||
|
|
|
|
R3 |
||||||||||
8
Electrostatic Energy.
Area of a spherical surface |
|
|
|
|
S 4 R2 |
|
|
|
|
|
|
|
||||
Energy: |
|
|
2 V |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
WE 1 |
|
UD D U dV |
|
|
|
|
|
|
|
||||||
R D ~ |
1 |
U |
~ |
1 |
|
|
|
|
~ |
1 |
R |
2 |
0 |
|||
R |
2 |
R |
|
|
UDdS |
R |
3 |
|
||||||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
||||
|
|
|
|
|
|
W |
2 V |
|
|
Finally we get: |
1 |
D EdV |
||
E |
|
|
|
|
|
|
|
|
|
9
Volume energy density.
|
|
|
|
|
|
|
W |
|
2 V |
|
|
Total energy: |
E |
1 |
D EdV |
||
|
|
|
|
||
|
|
|
Energy per unit volume: |
dWE |
WE D E |
|
dV |
2 |
For isotropic medium: |
D E |
WE |
E |
2 |
|
[J/m3] |
|
|
|
||
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
10