Оглавление

Лекция 1. Fundamental concepts of electromagnetics. Electrostatics. (Начало электростатики) 3

Лекция 2. Boundary conditions for the Laplace or Poisson equations (Граничные уравнения для уравнений Лапласа и Пуассона) 13

Лекция 3. Static magnetic field (Статическое магнитное поле) 23

Лекция 4. Method of images (метод зеркальных изображений) 33

Лекция 5. Solution of Laplace’s equation by separation of variables. (Решение уравнения Лапласа методом разделения переменных) 56

Лекция 6. Time dependent electromagnetic fields (Зависящие от времени электрические поля) 71

Лекция 7. Time dependent electromagnetic fields. (Зависящие от времени электрические поля) 84

Лекция 8. Numerical Methods of the Electromagnetic Field Modeling. (Численные методы моделирования электромагнитного поля) 99

The general course has a name of "Analysis and computation of electromagnetic fields".

В основном Калимов читает формулы а-ля volume integral from point a to point b from scalar product E and dl is equal to difference of potential, поэтому учитесь читать формулы. И когда он что-то пояснял, то я записывал исключительно за ним, так что что-то может быть не очень правильно с точки зрения английского языка.

Лекция 1. Fundamental concepts of electromagnetics. Electrostatics. (Начало электростатики)

Vectors and scalar fields. (Векторные и скалярные поля)

We need to remember some basement, which is used to describe any kind of electromagnetic interactions and dependences.

If some quantity (vectors and scalars) of something is distributed in the space have different values in different points then we can talk about them as a about fields. In this context the field is not an electromagnetic field. It is a distribution of the variable over the space. Field may be scalar (potential) and vector (electric field intensity). And there are main operations with vectors.

Operations with vectors. Addition and subtraction. (Операции с векторами, сложение и вычитание)

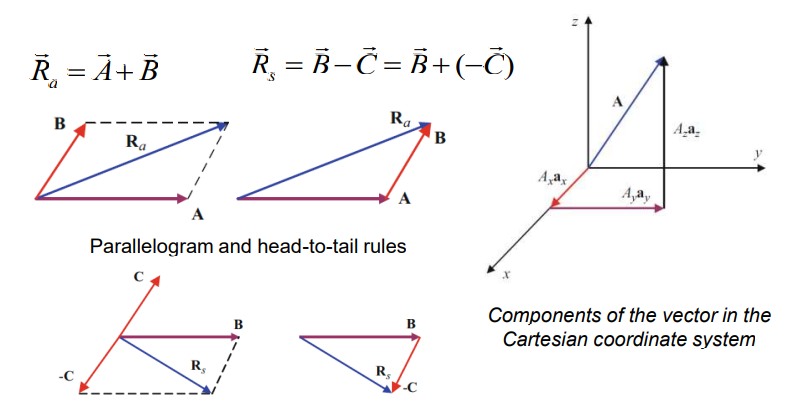
There are two ways to add two vectors: parallelogram and head-to-tail (triangle) rules.

Vector multiplication. Dot product. (Произведение векторов, скалярное произведение)

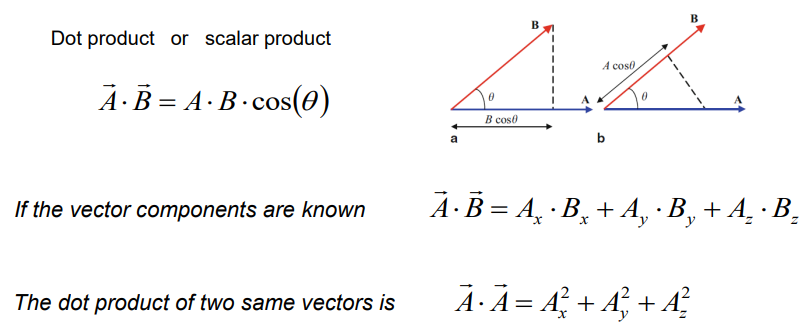
Dot product = scalar product = скалярное произведение.

The result of dot product is scalar value.

Читается как "A times B equal to …"

In Cartesian (Декартова) coordinate system , a dot product equals a sum of dot product vector's components.

Vector multiplication. Cross product. (Произведение векторов, векторное произведение)

Cross product = vector product = векторное произведение.

The result of cross product is vector value. It may be calculated using determinant of the third order which consist of unit vectors, lines with components of vectors.

Differential operations. Gradient of a scalar field. (Дифференциальные операторы, градиент скалярного поля)

Object of operation is a scalar field. Result of operation is a vector field.

Designation (обозначение): . Треугольник = nabla.

In the Cartesian coordinate system: 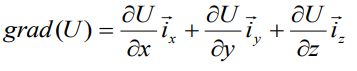there is sum of three terms.

Divergence of a vector field. (Дивергенция векторного поля)

Object of operation is a vector field. Result of operation is a scalar field.

Designation: . It is the scalar product of two operators: nabla and vector A.

In the Cartesian coordinate system: 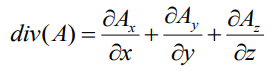it is a sum of three derivatives of three vector's components.

Circulation of a vector field. (Ротор векторного поля)

Object of operation is a vector field. Result of operation is a vector field.

"nabla cross vector A"

In the Cartesian coordinate system: 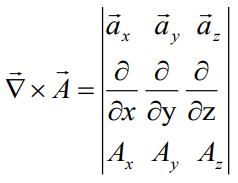, first line is line of unit vectors, instead of nabla vector we have three different derivatives, and the last line is vector's components.

.

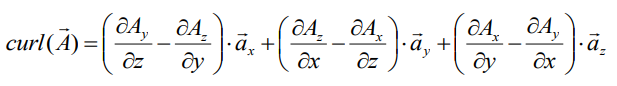Properties of the differential operators. (Свойства дифференциальных операторов)

Differential operations are linear:

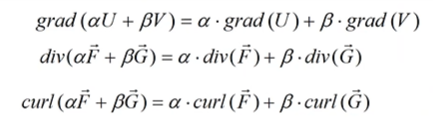
We can move constant multiplier through the operator. And gradient (or other) sum of two function we can split on sum of two gradients (or other).

Important vector identities: .

Divergence of the curl of F vector is equal to zero. Curl of a gradient of U is equal to zero. (Наверно как-то так читается.)

Differential operator Nabla. (Дифференциальный оператор Набла)

In the vector algebra an operator is often used.

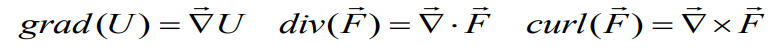
In the Cartesian coordinate syste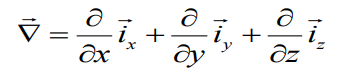m: . In other systems it has a different form.

Integral theorems. (Интегральные теоремы/интегральная форма теорем)

Different forms of the Gauss theorem (it is exclusively mathematical theorem) – integral from divergence of any kind of vector E is equal to the integral over the surface of this volume V over the scalar product of E and dS everywhere:

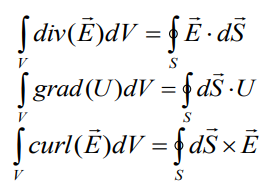
Other two forms of Gauss theorem for two other operators are represented.

Consequence of Gauss theorem is a Stoke’s theorem (not exactly, but it is the Gauss theorem for dimensional system):

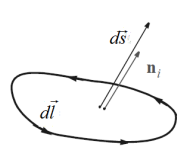
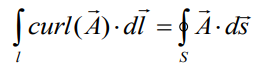
the curl of A integrated over the closed loop may be expressed as the integral over the surface which is limited by this loop from the scalar product of A and dS.