
Управление самолетом в турбулентной атмосфере. Пентюхов В.И., Мищенко Е.В
.pdf
МИНИСТЕРСТВООБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
В.И. Пентюхов Е.В. Мищенко А.М.Чашников
УПРАВЛЕНИЕ САМОЛЕТОМ
В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2005
1
УДК: 629.7.015
Пентюхов В.И., Мищенко Е.В., Чашников А.М. Управление самолетом в турбулентной атмосфере: Учеб.
.пособие. Воронеж: Воронеж. гос. техн. ун-т, 2005. 113 с.
В учебном пособии изложены вопросы управления возмущенным движением самолетом в турбулентной атмосфере с помощью двухканальных векторных систем управления.
Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 160200 “Авиастроение” и специальности 160201“Самолето-вертолетостроение”. дисциплине «Аэромеханика»
Учебное пособие подготовлено в электронном виде, в текстовом редакторе Word и содержится в файле «Управление самолетом в турбулентной атмосфере. rar»
Табл. = . Ил. . Библиогр. 20 назв.
Научный редактор канд. техн. наук, доц. Е.Н. Некравцев
Рецензенты: кафедра теоретической и прикладной механики Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. А.Н. Спорыхин), канд. техн. наук, доц. В.А. Шалиткин
Пентюхов В.И., Мищенко Е.В., Чашников А.М., 2005
Оформление. Воронежский государственный технический университет, 2005
2
ВВЕДЕНИЕ
Управление движением или полетом самолетов– это перевод самолета из одного возможного режима движения в другой посредством воздействия на параметры его движения.
Управление движением самолетов включает в себя выбор желаемой программы (траектории) полета и поддерживание (стабилизацию) выбранного режима полета.
Полет большинства самолетов проходит в плотных слоях атмосферы. Это пассажирские и транспортные самолеты, боевые самолеты, выполняющие полет на очень малых высотах, самолеты вертикального взлета и посадки (СВВП).
Но в плотных слоях атмосферы, как известно, существует турбулентность атмосферы, обусловленная перемещением воздушных масс. Она вызывает так называемую «болтанку самолетов, которая проявляется, в основном, в колебаниях их перегрузки.
Причем, эти колебания перегрузки могут достигать весьма больших величин. Особенно это относится к нормальным перегрузкам, возникающим при действии на самолет вертикальных порывов.
Так при полетах в турбулентной атмосфере пассажирские и транспортные самолеты неоднократно испытывали действие нормальных перегрузок порядка 1,0 g и даже выше (см. [11] и др.).
Но действие на самолет больших дополнительных перегрузок является весьма нежелательным и с точки зрения обеспечения безопасности полета, работоспособности экипажа и самочувствия пассажиров, поддержания заданной траектории полета, точности стрельбы, бомбометания и сброса грузов, а также с точки зрения конструктивной прочности самолета и характеристик усталости его конструкции.
Таким образом, турбулентность отрицательно сказывается на управлении движением летательных аппаратов.
Поэтому исследование управления движением летательных аппаратов в турбулентной атмосфере совместно с формированием и анализом структурных схем систем управления, обеспечивающих
3
существенное снижение величины турбулентных возмущений параметров движения, и, в первую очередь, нормальной перегрузки, является одной из актуальных задач управления движением летательных аппаратов
Естественно, что для исследования поведения летательных аппаратов в турбулентной атмосфере необходимо иметь математическую модель такой атмосферы.
Исследование физики атмосферы показывает, что турбулентность в атмосфере возникает по многим причинам и носит случайный характер.
Поэтому наиболее объективная оценка возмущений параметров движения летательных аппаратов может быть получена, если турбулентность атмосферы рассматривать с точки зрения теории случайных процессов (см. [5], [6] и др.).
В ряде работ на основании той или иной математической модели показано, что системы управления продольным движением, имеющие одну поверхность управления (руль высоты) и обеспечивающие парирование турбулентных возмущений перегрузки за счет изменения величины подъемной силы путем разворота самолета, обладают малой эффективностью.
С их помощью турбулентные возмущения перегрузки в центре тяжести самолета можно снизить не более чем на 30 - 40%
(см. [5], [6],[7] и др.).
Это связано с тем, что турбулентное возмущение перегрузки возникает одновременно с действием порыва, в то время как его парирование, осуществляемое этими системами управления, происходит в силу большой инерционности самолетов, со значительным запаздыванием.
Повышение быстродействия таких систем управления за счет увеличения их передаточных коэффициентов не приводит к существенному снижению величины турбулентных возмущений перегрузки в центре тяжести самолета и в то же время вызывает значительный рост дополнительных перегрузок, обусловленных угловыми ускорениями самолета.
Более эффективно парируют турбулентные возмущения перегрузки системы управления, имеющие дополнительные управляющие поверхности на крыльях (закрылки, флапероны), отклонение которых непосредственно изменяет величину подъемной силы самолета.
4
Если в таких системах управления отклонения руля высоты и закрылков согласованы, то они могут быть названы двухканальными векторными системами управления, так как они непосредственно изменяют величину подъемной силы без изменения углового положения самолета.
Непосредственное управление подъемной силой осуществляется с помощью специальных поверхностей условно называемых закрылками.
Под закрылками в данном случае понимаются поверхности управления, расположенные на некоторой части крыльев вдоль задней кромки и отклоняющиеся автоматически как вниз так и вверх от нейтрального положения по командам, вырабатываемым системой управления так, что при действии порыва, направленного вверх, закрылки также отклоняются вверх, и, наоборот.
Двухканальность этой системы управления обеспечивается использованием, кроме закрылков, также и руля высоты, на который подается специальный сигнал, пропорциональный отклонению закрылков
Поэтому этим системам управления в учебном пособии уделяется основное внимание. При этом учитывается наличие в них нелинейных элементов.
Так как уравнения продольного возмущенного движения самолета с двумя поверхностями управления могут быть линеаризованы по методу малых возмущений, [15],[16], то турбулентные возмущения параметров движения самолета (перегрузки и угловой скорости тангажа), поступающие на вход нелинейных элементов, можно рассматривать как результат линейного преобразования возмущения угла атаки, вызванного вертикальными порывами.
Но, как известно [9], любое линейное преобразование случайного процесса, имеющего нормальный закон распределения вероятностей, также приводит к случайному процессу с нормальным законом распределения вероятностей.
Случайным сигналом на выходах нелинейных элементов будет соответствовать закон распределения вероятностей, отличный от нормального, даже если на их входы поступают случайные сигналы с нормальным законом распределения вероятностей.
5
В замкнутой системе, какой является самолет и рассматриваемая система двухканального векторного управления, это может, в свою очередь, привести к отклонению распределения случайных возмущений на входах нелинейных элементов от нормального закона.
Но в данном случае этого не произойдет, так как сигналы с выходов нелинейных элементов поступают на вход самолета, который, являясь фильтром низких частот, нормализует их.
В результате этого турбулентные возмущения параметров движения самолета, несмотря на нелинейную систему управления, будут отвечать закону распределения вероятностей, весьма близкому к нормальному.
Таким образом, можно считать, что при полетах в турбулентной атмосфере возмущения перегрузки и угловой скорости тангажа, поступавшие на входы нелинейных элементов системы управления, имеют нормальный закон распределения вероятностей.
Следовательно, метод статистической линеаризации вполне применим для приближенного анализа эффективности рассматриваемых двухканальных векторных систем управления.
Как известно [9], суть метода статистической линеаризации состоит в приведении заданного нелинейного элемента, параметры которого, естественно, зависят от статистических характеристик входного сигнала, к некоторому эквивалентному в статистическом смысле линейному элементу.
Это позволяет при исследовании замкнутых двухканальных нелинейных систем управления применять разработанные методы анализа линейных систем управления.
Применение общих принципов теории статистической линеаризации к рассматриваемым двухканальным системам векторного управления позволило получить систему нелинейных алгебраических уравнений для определения коэффициентов статистической линеаризации нелинейных элементов и разработать методику ее решения, а также разработать методику определения коэффициента связи между каналами.
В учебном пособии изложена также методика исследования комбинации самолет – двухканальная система векторного управления на ее инвариантность относительно порывов.
6
1. РАБОТА В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ ДВУХКАНАЛЬНОЙ ВЕКТОРНОЙ СИСТЕМЫ НЕПОСРЕДСТВЕННОГО УПРАВЛЕНИЯ
ПОДЪЕМНОЙ СИЛОЙ.
1.1. Уравнения двухканальной векторной системы непосредственного управления
подъемной силой
Рассмотрим укрупненную структурную схему двухканальной векторной системы непосредственного управления подъемной силой (системы с двумя поверхностями управления) с учетом ограничений, налагаемых по ряду аэродинамических соображений на предельно допустимые углы отклонения поверхностей управления [12].
Характерной особенностью этой схемы является введение с помощью коэффициента 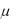 связи между каналами.
связи между каналами.
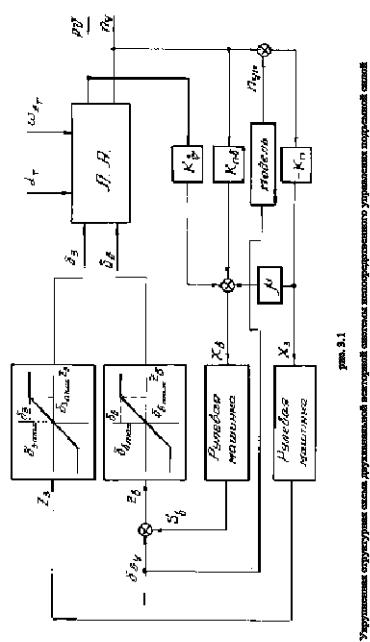
Эта схема приведена на рис. 1.1, где введены следующие обозначения:
T - возмущение угла атаки, вызванное действием на
самолет вертикальных порывов;
ZT - возмущение угловой скорости тангажа, вызванное
действием на самолет вертикальных порывов; n y - перегрузка в центре тяжести самолета;
n yм - значение перегрузки на выходе модели; p - угловая скорость тангажа самолета;
K p - передаточный коэффициент системы управления по угловой скорости тангажа;
Knв - передаточный коэффициент системы стабилизации по перегрузке в канале управления рулем высоты;
Kn - передаточный коэффициент системы стабилизации по
перегрузке в канале управления закрылками; - коэффициент связи между каналами управления
закрылками и рулем высоты;
7
8

в - сигнал на входе рулевой машинки руля высоты; 3 - сигнал на входе рулевой машинки закрылков;
s в - угол отклонения руля высоты рулевой машинкой; в у - управляющее воздействие руля высоты;
z в - потребный угол отклонения руля высоты;
в - располагаемый угол отклонения руля высоты; z3 - потребный угол отклонения закрылков;
3 - располагаемый угол отклонения закрылков.
Приведенная на рис. 1.1 двухканальная векторная система непосредственного управления подъемной силой является нелинейной как в силу ограничений, налагаемых на предельно допустимые углы отклонения поверхностей управления, так и в силу того, что реальные рулевые машинки имеют существенно нелинейные характеристики [2].
При этом нелинейность характеристик рулевых машинок связана, в первую очередь, с ограничением максимальной скорости движения штока и наличием зовы нечувствительности.
Величина максимальной скорости движения штока определяется в основном допустимой массой и габаритами рулевой машинки, а зона нечувствительности есть результат неизбежного конструктивного и производственного отклонения реальной рулевой машинки от идеально возможной.
Исходя из этого, рулевую машинку с жесткой обратной связью можно представить как замкнутую систему, состоящую из двух звеньев (рис. 1.2) –
Безинерционного нелинейного вена с насыщением и зоной нечувствительности и интегрирующего звена с постоянной времени
Т, охваченных K обр I или нет Kобр 0 отрицательной
обратной связью.
При этом, поскольку существующие рулевые машинки имеют весьма малую зону нечувствительности, а применение вибрационной линеаризации позволяет в ряде случаев практически совсем ее устранить [10], то основное влияние на нелинейность характеристики рулевой машинки оказывает ограничение максимальной скорости перемещения ее штока.
9
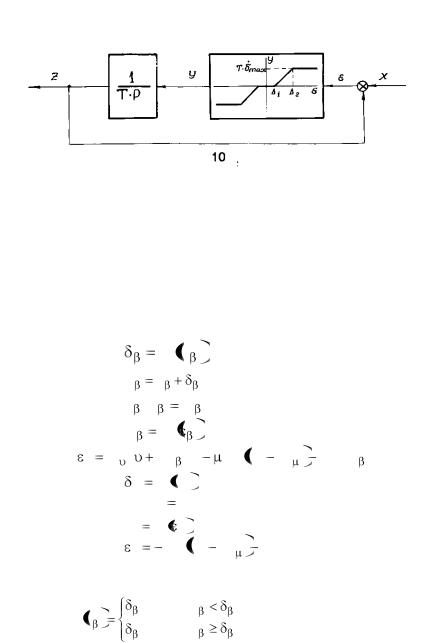
Рис. 1.2 Структурная схема рулевой машинки с жесткой обратной связью
Объединяя структурные схемы, приведенные на рис. 1.1 и 1.2, получим развернутую структурную схему системы непосредственного управления подъемной силой, которая изображена на рис. 1.1.
Этой структурной схеме соответствуют следующие нелинейные уравнения, описывающие законы управления рулем высоты и закрылками.
|
|
f1 Z ; |
|
|
|
|
(1.1) |
|
Z |
|
S |
y ; |
|
|
|
|
(1.2) |
T pS |
У ; |
|
|
|
|
(1.3) |
||
У |
|
f2 |
; |
|
|
|
|
(1.4) |
3 K p |
|
K n |
n y |
K n n y n y |
KобрS ; |
(1.5) |
||
3 |
|
f1 z3 ; |
|
|
|
|
(1.6) |
|
T3pz3 |
y3; |
|
|
|
|
(1.7) |
||
y3 |
f2 |
3 ; |
|
|
|
|
(1.8) |
|
3 |
|
K n n y |
n y |
|
Kобрz3; |
|
(1.9) |
|
где |
|
|
|
|
|
|
|
|
f1 z |
|
при z |
max , |
|
|
(1.10) |
||
|
при z |
|
, |
|
|
|
||
|
max |
max |
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
10 |
|
|
|
|
|
