2.2.2. Контактная разность потенциалов

Важным параметром p-n-перехода является контактная разность потенциалов U_к = U₀ = φ₀. Можно рассчитать контактную разность потенциалов, используя энергетическую диаграмму p-n-перехода.

Рис. 2.4. Энергетическая диаграмма p‑n-перехода

в состоянии термодинамического равновесия

Из рис. 2.4 следует, что величина потенциального барьера

qU₀ = qφ_о = (E_ip – E_Fp) – (E_Fn - E_in),

(2.1)

Учитывая, что формулы, определяющие концентрации основных носителей через уровень Ферми данного полупроводника и уровень Ферми собственного полупроводника и концентрацию носителей в собственном полупроводнике имеют вид

(2.2)

и, что

(2.3)

получаем, что контактная разность потенциалов или высота потенциального барьера

. (2.4)

2.2.3. Ширина p-n-перехода

Другим важным параметром p-n-перехода является его ширина, обозначенная W = W_p + W_n. Для нахождения W можно воспользоваться уравнением Пуассона. Уравнение Пуассона описывает связь электрического поля и потенциала в p-n-переходе. В одномерном приближении это уравнение имеет вид

, (2.5)

где (x) – зависимость потенциала от координаты; (x) – плотность объемного заряда; _s – диэлектрическая проницаемость полупроводника; ₀ – диэлектрическая постоянная.

Для решения этого уравнения выберем начало координат в области металлургического p-n-перехода. При этом донорный полупроводник будет находиться в области x > 0 (в дальнейшем обозначим цифрой I), а акцепторный – в области x < 0 (в дальнейшем обозначим цифрой II).

Заряд в ОПЗ p‑n-перехода для полупроводника n-типа обусловлен зарядом ионизованных доноров с плотностью N_D⁺_, для полупроводника p-типа – зарядом ионизованных акцепторов с плотностью N_A⁺. Поэтому для области I , для области II . Будем решать уравнение Пуассона отдельно для областей I и II. После интегрирования уравнения Пуассона получаем для области I:

, (2.6)

для области II:

. (2.7)

Знак минус в выражениях (2.6), (2.7) указывает, что направление электрического поля противоположно направлению оси x.

Из соотношений (2.6) и (2.7) следует, что электрическое поле Е максимально на металлургической границе p-n-перехода (x = 0), линейно спадает по области пространственного заряда и равно нулю на границах ОПЗ – квазинейтральный объем полупроводника (x = W_n; x = W_p).

Максимальная величина электрического поля E_max будет равна

. (2.8)

Для нахождения распределения потенциала (а, следовательно, и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.7) при следующих граничных условиях: x = W, (W) = 0. Получаем

. (2.9)

Используя граничные условия , находим константу интегрирования:

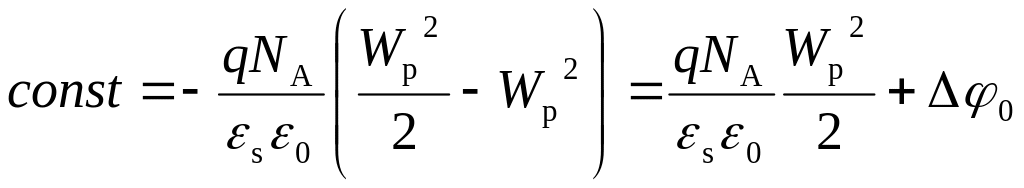. (2.10)

Подставляя полученные значения константы в соотношение (2.9), получаем для распределения потенциала (x) в области x < 0:

. (2.11)

Проводя аналогичное интегрирование для области x > 0, получаем

. (2.12)

Используя граничные условия , для константы интегрирования в этой области получаем:

. (2.13)

Подставляя полученные значения константы в соотношение (2.12), получаем для распределения потенциала (x) в области x > 0:

. (2.14)

Таким образом, закон изменения потенциала  в p-области (отсчет идет от уровня в квазинейтральной области):

, x < 0, (2.15)

и, наоборот, в n-области:

, x > 0. (2.16)

На рис. 2.5 приведена диаграмма, иллюстрирующая распределение электрического поля и потенциала в p-n-переходе, рассчитанная по соотношениям (2.6), (2.7), (2.15) и (2.16).

Рис. 2.5. Диаграмма, иллюстрирующая распределение

электрического поля и потенциала в p-n-переходе:

а - структура p-n-перехода; б - распределение электрического поля в ОПЗ; в - распределение потенциала в ОПЗ

На металлургической границе p-n-перехода при x = 0 значение потенциала ₁ + ₂ = ₀ = _n0 + _p0, или

. (2.17)

Согласно уравнению электронейтральности в замкнутых системах величины положительного и отрицательного заряда на единицу площади должны быть равны:

. (2.18)

Следовательно,

. (2.18, а)

Подставляем выражение (2.18, а) в (2.17), получаем

.

Несложные преобразования позволяют получить выражение для ширины обедненных областей W_p и W_n в p- и n-областях соответственно:

. (2.19)

Из предыдущих формул легко видеть, что с ростом легирования p-области ширина p-n-перехода W_p в акцепторной части полупроводника уменьшится.

Полная ширина p-n-перехода W, равная W = W_p + W_n, будет вычисляться по формуле

. (2.20)

Для несимметричных p⁺-n-переходов (концентрация акцепторов существенно больше концентрации доноров) из соотношений (2.18) и (2.18, а) следует, что ширина обедненной области в полупроводнике p-типа будет существенно меньше, чем ширина обедненной области в полупроводнике n-типа:

.

Таким образом, вся обедненная область p⁺-n-перехода сосредоточена в области с низким значением концентрации легирующей примеси W = W_n.

Формула (2.20) определяет полную толщину резкого p-n-перехода. Реальные p-n-переходы бывают несимметричными, то есть или , поэтому толщина резкого несимметричного p‑n-перехода

, (2.21)

где N – концентрация примеси в слаболегированной области.

Толщина плавного p-n-перехода с линейным распределением примеси

, (2.22)

где а – градиент концентрация примеси.