
- •Введение
- •1. Физические основы работы приборов твердотельной электроники
- •1.1. Зонная структура полупроводников
- •1.2. Собственные и примесные полупроводники
- •1.3. Статистика электронов и дырок в полупроводниках. Концентрация носителей заряда и положение уровня Ферми
- •1.4. Концентрация электронов и дырок в собственном полупроводнике
- •1.5. Концентрация электронов и дырок в примесном полупроводнике
- •1.6. Определение положения уровня Ферми
- •1.7. Проводимость полупроводников
- •1.8. Токи в полупроводниках
- •1.9. Неравновесные носители. Генерация и рекомбинация носителей
- •1.10. Уравнение непрерывности
- •1.11. Электрические поля в кристаллах
- •2. Контактные явления
- •2.1. Разновидности электрических переходов и контактов
- •2.2. Электронно-дырочный переход
- •Равновесия
- •2.2.2. Контактная разность потенциалов
- •2.2.3. Ширина p-n-перехода
- •2.2.4. Прямое включение р-n-перехода
- •2.2.5. Уровень инжекции
- •2.2.6. Обратное включение р-n-перехода
- •2.2.7. Теоретическая вольт-амперная характеристика
- •2.2.8. Вольт-амперная характеристика реального
- •2.2.9. Вольт-амперная характеристика р-п-перехода в полулогарифмических координатах
- •2.2.10. Пробой р-п-перехода
- •2.2.11. Емкость p-n-перехода
- •2.2.12. Переходные процессы в p-n-переходах
- •2.2.13. Частотные свойства p-n-перехода
- •2.2.14. Эквивалентные схемы р-п-перехода
- •2.2.15. Влияние температуры на свойства
- •2.3. Разновидности электрических переходов
- •2.3.1. Гетеропереходы
- •2.3.2. Контакт полупроводников с одним типом электропроводности
- •2.3.3. Контакт металл – полупроводник. Барьер Шоттки
- •2.3.4. Омические контакты
- •2.3.5. Явления на поверхности полупроводников
- •3.2. Область пространственного заряда в равновесных условиях
- •3.3. Приповерхностная область пространственного заряда
- •3.4. Распределение плотности пространственного заряда, электрического поля и потенциала в идеальной
- •3.5. Вольт-фарадные характеристики идеальной
- •3.5.1. Емкость области пространственного заряда
- •3.5.2. Емкость мдп-структур
- •3.6. Компоненты заряда в реальном диоксиде кремния и их влияние на вфх мдп-структуры
- •3.7. Распределение плотности пространственного заряда, электрического поля и потенциала в реальной
- •3.8. Определение параметров мдп-структур на основе анализа c-V характеристик
- •4. Полупроводниковые диоды
- •4.1. Методы изготовления полупроводниковых диодов
- •4.2. Выпрямительные диоды
- •4.3. Варикапы
- •4.4. Стабилитроны
- •4.5. Туннельный и обращенный диоды
- •4.6. Высокочастотные и сверхвысокочастотные диоды
- •4.7. Импульсные диоды
- •5. Биполярные транзисторы
- •5.1. Структура и основные режимы работы
- •5.2. Схемы включения транзистора
- •5.3. Основные физические процессы в биполярных транзисторах
- •5.4. Модуляция сопротивления базы
- •5.5. Статические характеристики биполярных транзисторов
- •Как четырехполюсник
- •5.6. Эквивалентная схема биполярного транзистора
- •5.7. Дифференциальные параметры биполярных транзисторов в схеме с общей базой
- •5.8. Дифференциальные параметры биполярных транзисторов в схеме с общим эмиттером
- •5.9. Малосигнальные параметры биполярного транзистора
- •5.9.1. Система z-параметров
- •5.9.2. Система y-параметров
- •5.9.3. Система h-параметров
- •5.10. Частотные и импульсные свойства транзисторов
- •6. Тиристоры
- •6.1. Структура и принцип действия
- •6.2. Основные параметры тиристоров
- •6.3. Феноменологическое описание вах динистора
- •6.4. Способы включения и выключения тиристоров
- •7. Полевые транзисторы и приборы с зарядовой связью
- •7.1. Полевой транзистор с управляющим p-n-переходом
- •7.3. Эффект смещения подложки
- •7.4. Эквивалентная схема мдп‑транзистора
- •7.5. Подпороговые характеристики мдп-транзистора
- •7.6. Приборы с зарядовой связью
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
3.8. Определение параметров мдп-структур на основе анализа c-V характеристик
Анализ вольт-фарадных характеристик позволяет получить обширную информацию об основных параметрах МДП-структур: типе проводимости полупроводниковой подложки (n- или p-тип); концентрации легирующей примеси в подложке и законе ее распределения в приповерхностной области полупроводника; величине и знаке встроенного в диэлектрик МДП‑структуры заряда; толщине подзатворного окисла; плотности поверхностных состояний на границе раздела полупроводник – диэлектрик. Рассмотрим более подробно эти вопросы.
Определение типа проводимости полупроводниковой подложки. Для определения типа проводимости подложки воспользуемся высокочастотной вольт-фарадной характеристикой. Как следует из вида высокочастотной C-V кривой при обогащении основными носителями, емкость МДП-структуры максимальна и определяется емкостью диэлектрика. В инверсии же емкость МДП-структуры минимальна. Таким образом, если максимум емкости C-V кривой лежит в более положительных напряжениях, чем минимум, то подложка изготовлена из полупроводника n‑типа, если же максимум C-V кривой находится в более отрицательных напряжениях, то подложка изготовлена из полупроводника p-типа. На рис. 3.13 приведены для примера высокочастотные ВФХ на n- и p-типах подложки.
Определение толщины подзатворного диэлектрика. Поскольку, как было показано ранее, в обогащении емкость МДП‑структуры определяется только геометрической емкостью диэлектрика Cox, то
![]() ,
(3.51)
,
(3.51)
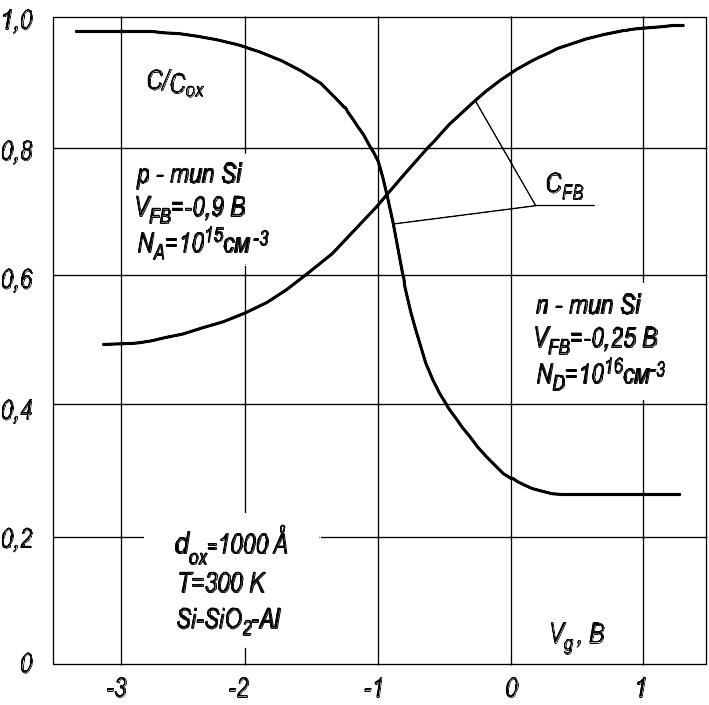
Рис. 3.13. Высокочастотные ВАХ МДП-структур, изготовленных на полупроводниковых подложках n- и p-типа
где εox – относительная диэлектрическая проницаемость окисла.
Отсюда следует, что
![]() ,
(3.52)
,
(3.52)
где Cox – удельная емкость подзатворного диэлектрика, то есть емкость на единицу площади.
Для подстановки в (3.52) экспериментальных значений необходимо сначала пронормировать емкость, то есть разделить экспериментальное значение емкости на площадь S МДП-структуры. При напряжениях на затворе VG – VFB (2 -3) В практически для всех МДП-структур полная емкость C только на 2 - 3 % отличается от емкости диэлектрика. Исключение составляют структуры со сверхтонким окислом dox < 100 Å, у которых в этой области VG становится существенным квантование в ОПЗ, и это отличие может достигать 10 %.
Определение величины и профиля концентрации легирующей примеси. Для определения величины концентрации легирующей примеси воспользуемся следующим свойством высокочастотных C - V характеристик МДП-структур: их емкость в области инверсии достигает минимальной величины Cmin и определяется только емкостью области ионизованных доноров CB и емкостью диэлектрика Cox. При этом
![]() .
(3.53)
.
(3.53)
Используя для емкости окисла Cox выражение (3.51) и для емкости области ионизованных акцепторов из (3.30), получаем
 .
(3.54)
.
(3.54)
Выражение (3.54) совместно с (3.30) для емкости ОПЗ ионизованных акцепторов приводит к выражению для концентрации легирующей примеси:
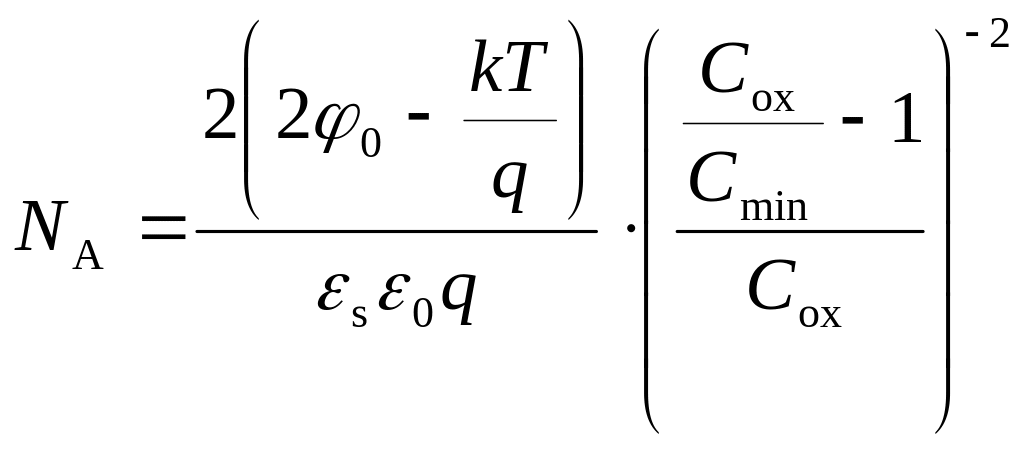 .
(3.55)
.
(3.55)
На рис. 3.14 приведена
номограмма зависимости нормированной
величины емкости
![]() от толщины dox
для систем Si - SiO2
с концентрацией легирующей примеси NA
в качестве параметра.
от толщины dox
для систем Si - SiO2
с концентрацией легирующей примеси NA
в качестве параметра.

Рис. 3.14.
Зависимость нормированной величины
емкости
![]() в минимуме высокочастотной ВАХ от
толщины подзатворного диэлектрика dox
при различных величинах концентрации
легирующей примеси для кремниевых
в минимуме высокочастотной ВАХ от
толщины подзатворного диэлектрика dox
при различных величинах концентрации
легирующей примеси для кремниевых
МДП-структур
Из рис. 3.14 видно, что чем меньше толщина диэлектрика и ниже концентрация легирующей примеси, тем больше перепад емкости от минимального до максимального значений наблюдается на ВФХ. Для определения профиля концентрации NA от расстояния вглубь полупроводника z воспользуемся высокочастотной C-V кривой, снятой в области неравновесного обеднения. Неравновесное обеднение возможно реализовать в том случае, когда период напряжения развертки меньше постоянной τ генерационного времени неосновных носителей в ОПЗ. В этом случае величина поверхностного потенциала может быть больше ψs > 2φ0, а ширина ОПЗ соответственно больше, чем ширина ОПЗ в равновесном случае. Возьмем также МДП-структуру с достаточно тонким окислом, таким, чтобы падением напряжения на окисле Vox можно было бы пренебречь по сравнению с величиной поверхностного потенциала, т.е. Vox << ψs; VG ≈ ψs. В этом случае тангенс угла наклона зависимости C-2 = f(VG) определит величину концентрации NA:
 (3.56)
(3.56)
Значение координаты z, которой соответствует рассчитанная величина NA, определяется при подстановке значения ψs = VG в выражение для ширины ОПЗ:
![]() .
(3.57)
.
(3.57)
В предельном
случае, когда толщина окисла
![]() ,
эту величину используют, измеряя
неравновесную емкость как емкость
барьеров Шоттки при обратном смещении.
,
эту величину используют, измеряя
неравновесную емкость как емкость
барьеров Шоттки при обратном смещении.
Определение
величины и знака встроенного заряда.
Для определения величины и
знака встроенного в диэлектрик
МДП‑структуры заряда обычно пользуются
высокочастотным методом ВФХ. Для этого,
зная толщину подзатворного диэлектрика
dox,
концентрацию легирующей примеси NA
и работу выхода материала затвора,
рассчитывают согласно (3.33) и (3.37)
теоретическое значение емкости плоских
зон CFB
МДП-структуры и напряжения плоских зон
VFB = Δφms.
Поскольку экспериментальная C-V
кривая высокочастотная, т.е.
![]() ,
то, проводя сечение C = const = CFB (теор.),
мы получаем при пересечении этой кривой
с экспериментальной ВФХ напряжение,
соответствующее ψs = 0,
т.е. экспериментальное напряжение
плоских зон VFB
(эксп.). При этом, согласно (3.46),
,
то, проводя сечение C = const = CFB (теор.),
мы получаем при пересечении этой кривой
с экспериментальной ВФХ напряжение,
соответствующее ψs = 0,
т.е. экспериментальное напряжение
плоских зон VFB
(эксп.). При этом, согласно (3.46),
![]() .
(3.58)
.
(3.58)
Если Qox, Qss > 0, то VFB (эксп.) > VFB (теор.), и наоборот, если Qox, Qss < 0, то VFB (эксп.) < VFB (теор.).
Таким образом, знак и величина суммарного заряда в плоских зонах определяются соотношением (3.58) однозначно. Для вычленения заряда в поверхностных состояниях воспользуемся тем, что он обусловлен основными носителями (p‑тип, Qss(ψs = 0) > 0 и n‑тип, Qss(ψs = 0) < 0), захваченными на поверхностные состояния. Зная величину Nss, можно рассчитать величину заряда в поверностных состояниях Qss и таким образом из (3.46) определить величину и знак встроенного в диэлектрик заряда Qox.
