3.3. Приповерхностная область пространственного заряда

Одной из основных задач при анализе области пространственного заряда полупроводника является нахождение связи между электростатическим потенциалом ψ(z), с одной стороны, и величинами заряда в области пространственного заряда Q_s, емкости ОПЗ C_s – с другой. Нахождение этой связи основано на решении уравнения Пуассона для ОПЗ.

Уравнение Пуассона для полупроводника p-типа

. (3.5)

Величина ρ(z) в общем случае, когда отсутствует ограничение на малость возмущения, принимает значение

. (3.6)

В квазинейтральном объеме, где условие электронейтральности выполняется, ρ(z) = 0.

Тогда

. (3.7)

Поскольку, как было показано в (3.2 – 3.4),

,

,

для ρ(z) в ОПЗ имеем

. (3.8)

Подставляя (3.8) в (3.5), имеем для нахождения ψ(z) дифференциальное уравнение

. (3.9)

Домножим выражение для дебаевской длины экранирования, которое представлено в главе 2 формулой (2.98), слева и справа на величину . Тогда левая часть выражения принимает вид

. (3.10)

Следовательно,

. (3.11)

Проинтегрировав (3.11) от бесконечности до некоторой точки ОПЗ, получаем

. (3.12)

Воспользовавшись определением дебаевской длины экранирования L_D (2.98), а также соотношением , получаем

. (3.13)

Обозначим

. (3.14)

Из (3.13) и (3.14) имеем

. (3.15)

Соотношение (3.15) называется первым интегралом уравнения Пуассона.

Знак электрического поля выбирается в зависимости от знака поверхностного потенциала. Если ψ_s > 0 (обеднение основными носителями или инверсия), поле направлено вглубь полупроводника по оси z и положительно. При ψ_s < 0 поле E направлено против оси z и отрицательно.

Величина электрического поля на поверхности

. (3.16)

Поскольку согласно теореме Гаусса величина электрического поля на поверхности E_s связана определенным образом с плотностью пространственного заряда на единицу площади Q_sc, имеем

. (3.17)

Выражение (3.17) для заряда в ОПЗ справедливо для любых значений поверхностного потенциала. Однако использование его для конкретных случаев довольно затруднено в силу громоздкости функции F(ψ, φ₀) в виде (3.14). На рис. 3.6 приведено значение заряда в ОПЗ Q_sc как функции поверхностного потенциала _s, рассчитанное для конкретного случая.

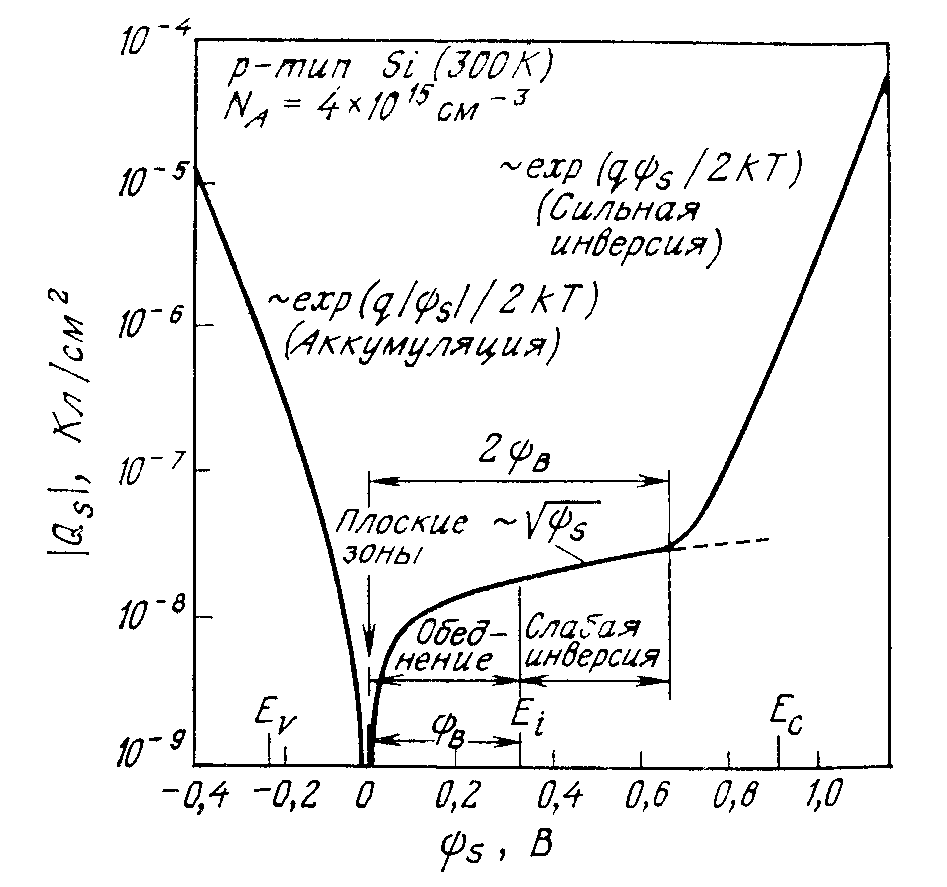
Рис. 3.6. Зависимость заряда в ОПЗ от поверхностного потенциала _s, рассчитанная для кремния p‑типа

3.4. Распределение плотности пространственного заряда, электрического поля и потенциала в идеальной

МДП-структуре в режиме сильной инверсии

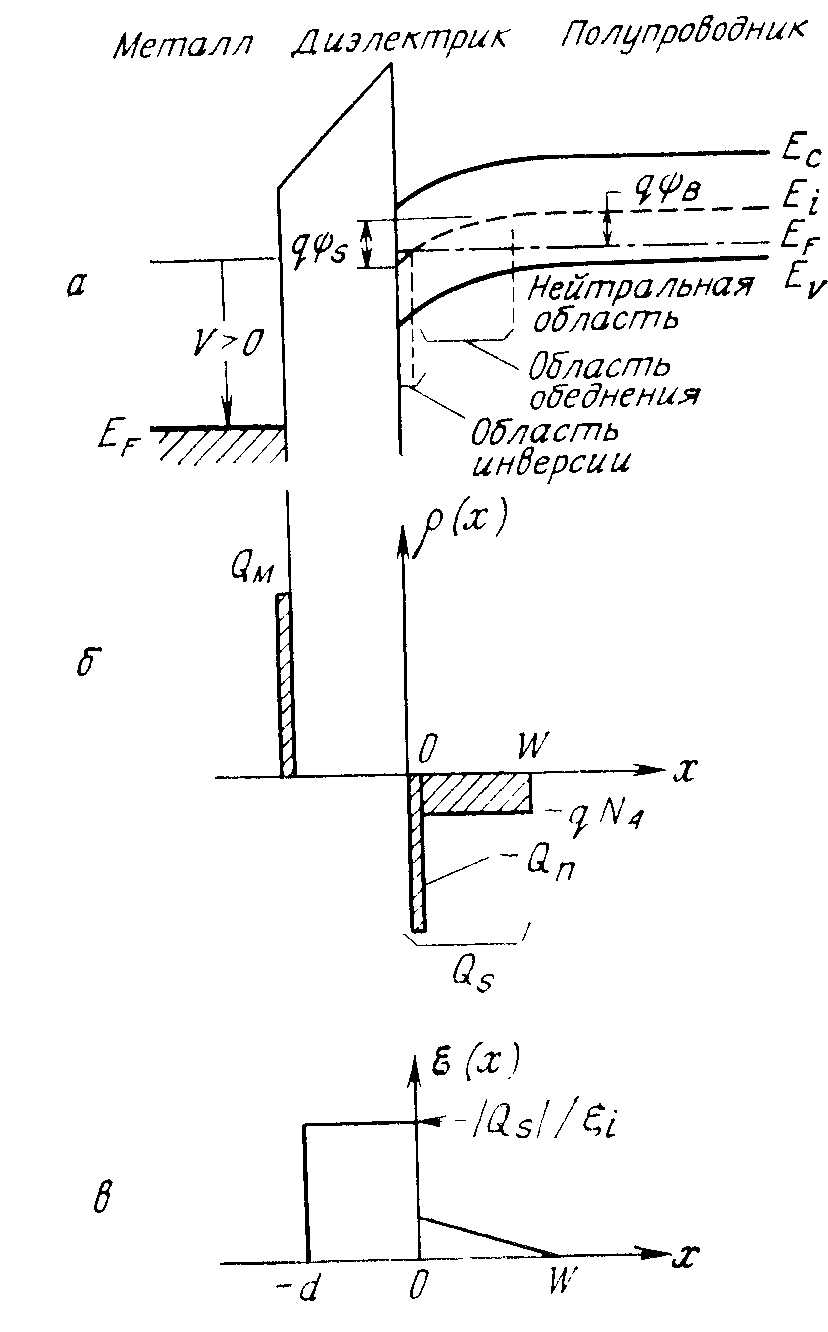
При смещениях, соответствующих режимам обеднения и инверсии, приложенное напряжение отталкивает дырки от поверхности, образуя обедненный слой, и индуцирует электроны, образующие инверсный слой. Зонная диаграмма идеальной МДП-структуры, с полупроводником р-типа в режиме сильной инверсии имеет вид, приведенный на рис. 3.7, а. На рис. 3.7, б приведено распределение заряда в структуре. Для обеспечения электронейтральности структуры заряд на ее металлическом электроде Q_M должен быть равен сумме электронного заряда в инверсном слое Q_inv = Q_n и заряда ионизированных акцепторов в области обеднения полупроводника:

Q_M = Q_inv + qN_aW = Q_inv + Q_B = Q_S. (3.18)

Все заряды отнесены к единице площади границы раздела, W – толщина обедненного слоя, Q_S – полная поверхностная плотность заряда в полупроводнике.

Распределение электрического поля (рис. 3.7, б) потенциала (рис. 3.7, г) соответствуют первому и второму интегралу уравнения Пуассона. Поле на границе между диэлектриком и полупроводником имеет разрыв, вследствие различных значений диэлектрической проницаемости граничащих материалов оно уменьшается от Е_i = Q_S/_i до Е_S. Напряженность поля в инверсном слое резко уменьшается по мере удаления от поверхности

(3.19)

В области обеднения электрическое поле межде подложкой и затвором однородное и описывается уравнением Пуассона

(3.20)

При режиме обеднения в полупроводнике возникает

г

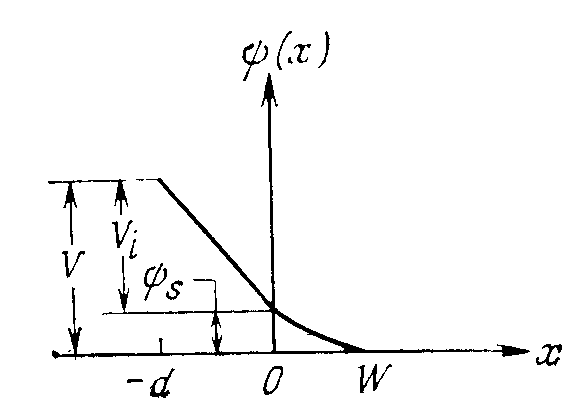
Рис. 3.7. Зонная диаграмма идеальной МДП-структуры (а), и распределение зарядов (в условиях инверсии) (б),

электрического поля (в) и потенциала (г)

ОПЗ, образованная отрицательными ионами акцепторной примеси, толщиной W. Плотность заряда в ОПЗ, отнесенная к единице объема  = - qN_a, уравнение Пуассона принимает вид

(3.21)

Интегрируя (3.21) с граничными условиями  = 0 и d /dх = 0, при х = W, получаем

(3.22)

В отсутствии разности работ выхода приложенное напряжение делится между полупроводником и диэлектриком, то есть V = V_i + (х), где V_i – падение напряжения на слое диэлектрика; (х) – падение напряжения в ОПЗ полупроводника. Решение уравнения Пуассона дает

(3.23)

где _s – поверхностный потенциал на границе раздела полупроводник - диэлектрик.

Падение напряжения на слое диэлектрика

V_i = Е_id = , (3.24)

Но с другой стороны сумма зарядов взятых на единицу площади на управляющем электроде (металле) Q_M и индуцированного пространственного заряда Q_S равна нулю Q_M + Q_S = 0. Удельная емкость диэлектрика С_i = _i₀/d, тогда

V_i = (3.25)

Таким образом, напряжение на металлическом электроде (затворе)

V_i = . (3.26)

Определим пороговое напряжение считая, что в инверсном слое отсутствуют подвижные носители заряда

. (3.27)

Пороговое напряжение – это напряжение на затворе при котором начинается режим сильной инверсии.