Контрольные вопросы и задания

1.1. Какие существуют этапы математического моделирования какого-либо объекта?

1.2. Что представляют собой объекты в моделируемой системе?

1.3. В чем заключается достоинство имитационного моделирования как метода исследования сложных систем?

1.4. В чем заключается принцип Гамильтона?

2. Классификация уравнений математической физики как моделей атмосферных процессов. Уравнение волновых движений

Подавляющее количество моделей атмосферных процессов формализуется в виде уравнений с распределенными параметрами. Поэтому в настоящем разделе будут рассмотрены основные понятия уравнений математической физики.

2.1. Понятие об общем решении уравнений в частных производных

Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Так, например:

1) при изучении различных видов волн – упругих, звуковых, электромагнитных, а также других колебательных явлений приходим к волновому уравнению

, (2.1)

где c – скорость распространения волн в данной среде;

2) процессы распространения тепла в однородном изотропном теле так же, как и явления диффузии, описываются уравнением теплопроводности:

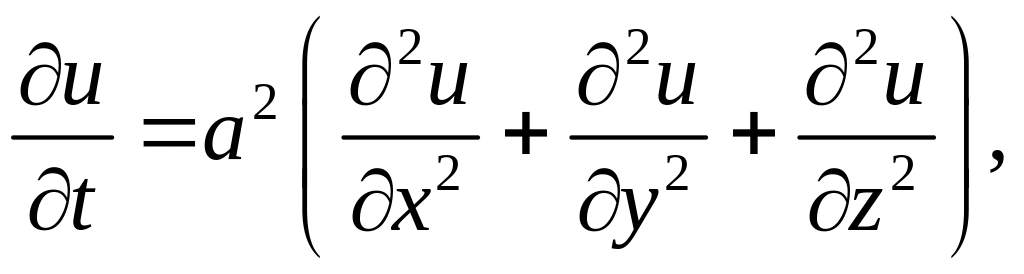(2.2)

3) при рассмотрении установившегося теплового состояния в однородном изотропном теле приходим к уравнению Пуассона:

. (2.3)

При отсутствии источников тепла внутри тела уравнение (2.3) переходит в уравнение Лапласа:

. (2.4)

Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют массы и, соответственно, электрические заряды.

Уравнения (2.1) – (2.4) называют основными уравнениями математической физики. Их подробное изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач.

Функция , удовлетворяющая какому-либо из уравнений (2.1 ) – (2.4), называется его решением.

Пусть дано уравнение

. (2.5)

Найдем его решение, т.е. функцию удовлетворяющую уравнению (2.5). Для этого запишем это уравнение в виде: . Поскольку производная по переменной от величины, стоящей в скобках, равна нулю, то последняя является некоторой произвольной функцией от y: . Поэтому Но, интегрируя произвольную функцию , получим новую, также произвольную функцию, скажем , плюс произвольная функция , которая играет роль произвольной постоянной интегрирования в теории обыкновенных дифференциальных уравнений. Таким образом, общий интеграл уравнения второго порядка (2.5)

содержит две произвольные функции.

Чтобы теперь из общего решения найти определенное частное решение, нужно найти конкретный вид функций и .

Однако в этом и состоит причина существенного различия методов решения обыкновенных дифференциальных уравнений в частных производных. Из-за чрезвычайной общности общего решения уравнения в частных производных, как правило, очень трудно из него выделить нужное конкретное решение.