Контрольные вопросы и задания

6.1. Может ли возникать хаос в реалистических моделях?

6.2. Что представляет собой модель Лоренца?

6.3. В каких задачах возможно применение системы уравнений Лоренца?

6.4. Что называют числом Прандтля и числом Рэлея?

6. Динамика системы лоренца

Система трех нелинейных уравнений первого порядка

(7.1)

описывает динамику нескольких физических систем – конвекцию в слое, конвекцию в кольцевой трубке и др. Ее называют моделью Лоренца по имени исследователя, обнаружившего в численных расчетах возможность хаотического поведения, а также глубоко и проницательно интерпретировавшего наблюдаемый режим непериодических колебаний. Данный раздел посвящен обсуждению динамики модели Лоренца.

1. Результаты численного моделирования уравнений Лоренца

Если взять выбранные Лоренцем в исходной работе значения параметров σ = 10, b = 8/3, r = 28 и провести численное решение уравнений (7.1) на компьютере, то обнаруживается, что в системе устанавливается хаотический автоколебательный режим. На рис. 7.1 приводятся зависимости динамических переменных х, у, z от времени. Показанную на верхней диаграмме зависимость х(t) можно интерпретировать наглядно, имея в виду модель водяного колеса. Именно участки процесса, отвечающие осцилляциям в области х > 0, отвечают вращению колеса в одну сторону, а участки х < 0 – в другую. Видно, что направление вращения время от времени меняется на противоположное, причем число оборотов (осцилляций) в определенном направлении от раза к разу меняется хаотически.

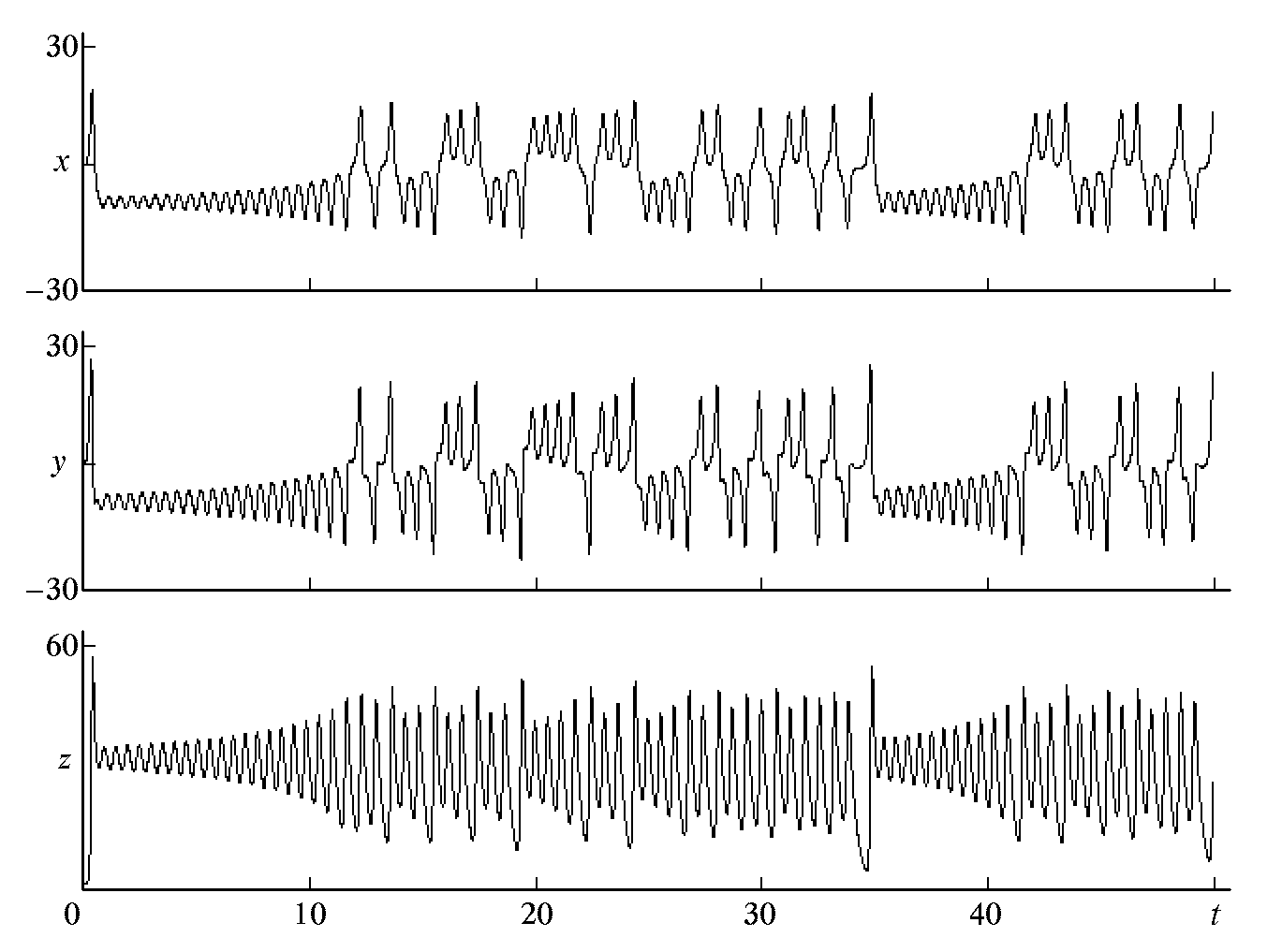
Рис. 7.1. Зависимости динамических переменных х, у, z от времени,

полученные численным интегрированием уравнений

Лоренца при σ = 10, b = 8/3, r = 28

На рис. 7.2 показан фазовый портрет системы Лоренца. Как можно видеть, фазовая траектория вырисовывает в пространстве состояний (х, у, z) некий объект сложной структуры, который похож на моток ниток, причем не перепутанных, а аккуратно уложенных одна вдоль другой. Это образование называют странным аттрактором или, в контексте данной конкретной системы, аттрактором Лоренца.

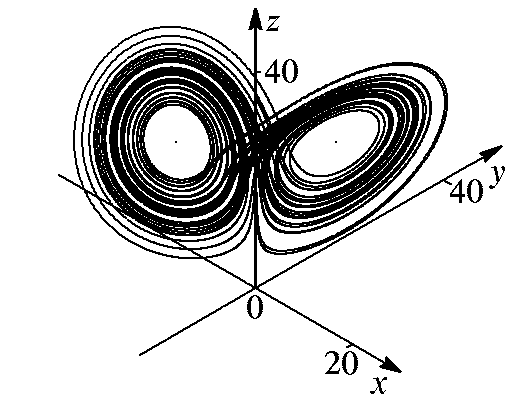
Рис. 7.2. Фазовый портрет аттрактора Лоренца для «классического»

набора параметров: σ = 10, b = 8/3, r = 28

Как можно проверить, при указанных «классических» значениях параметров σ, b, r один и тот же установившийся режим (по крайней мере, в смысле усредненных статистических характеристик и в смысле стационарности внешнего вида аттрактора) возникает в системе Лоренца независимо от выбора начальных условий.

В своей работе Лоренц вскрывает динамическую природу наблюдаемого хаотического поведения при помощи замечательно простого и эффектного приема. Рассмотрим зависимость переменной z от времени и занумеруем ее максимумы в порядке следования во времени. Далее обработаем результаты численного решения уравнений, построив график зависимости величины очередного максимума от предыдущего, (рис. 7.3, а).

Совсем не очевидно, что эта процедура приведет к какому-то разумному результату, но это так! Оказывается, что точки хорошо ложатся на определенную кривую с острой вершиной. Но тогда мы можем заменить исследование динамики исходных уравнений Лоренца гораздо более простой задачей – анализом динамики одномерного отображения !

Это отображение очень похоже на отображение «тент» (рис. 7.3, б), которое демонстрирует хаотическую динамику и для которого множество возможных траекторий допускает кодирование всевозможными последовательностями двух символов.

Можно показать, что такими же свойствами обладает и отображение . Это веский довод в пользу динамической природы хаоса, наблюдаемого в модели Лоренца. Оговоримся, однако, что отсюда еще довольно далеко до строгого математического доказательства, поскольку связь между исходной системой и одномерным отображением более тонка, чем это может показаться на первый взгляд.

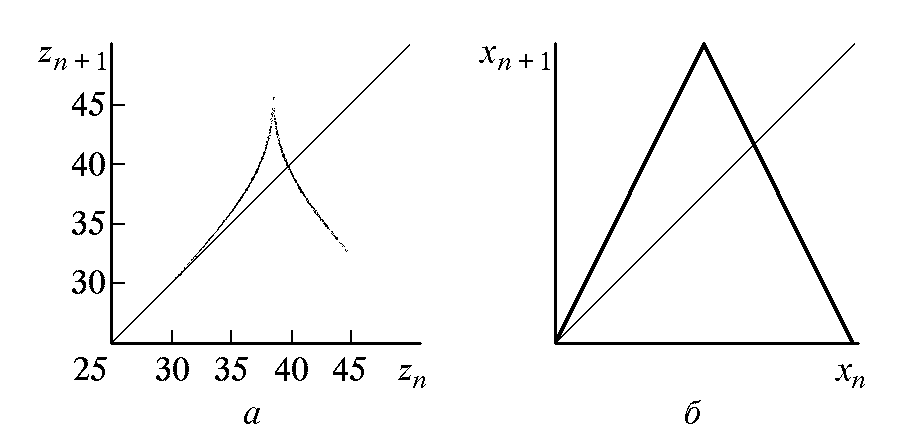
Рис. 7.3. Отображение, полученное численно для системы Лоренца (а),

и показанное для сравнения отображение «тент» (б)

К диаграмме рис. 7.3 можно прийти из следующих рассуждений. Условие появления экстремума переменной z(t) отвечает равенству нулю ее производной, которая, согласно третьему уравнению (7.1), равна ху – bz. Уравнение ху – bz = 0 определяет в фазовом пространстве некоторую поверхность Н (гиперболический параболоид). Выделим на этой поверхности область H такую, что выполняется дополнительное условие наличия именно максимума: . Поток фазовых траекторий системы Лоренца задает на этой части поверхности отображение Пуанкаре. Выпустив траекторию из произвольной точки А области дождемся ее следующего пересечения с – это и будет образ точки А. Говоря формально, отображение Пуанкаре двумерное и к одномерному отнюдь не сводится. Более тщательный анализ показывает, однако, что точки на графике в действительности не ложатся на определенную кривую, а имеют некоторый разброс, связанный с присущей аттрактору Лоренца фрактальной поперечной структурой.