Контрольные вопросы и задания

7.1. В чем состоят результаты численного моделирования уравнений Лоренца?

7.2. В чем особенность ограниченности системы Лоренца?

7.3. Поясните диссипативность системы Лоренца.

6. Неподвижные точки. Устойчивость. Бифуркация

1. . Неподвижные точки

Найдем неподвижные точки системы уравнений Лоренца. Это состояния, не меняющиеся во времени, т. е. производные динамических переменных по времени надо приравнять нулю. Следовательно, правые части уравнений тоже должны обращаться в нуль. Это дает три алгебраических уравнения для трех неизвестных:

(8.1)

Из первого уравнения имеем , тогда второе переписывается в виде и видно, что есть две возможности и . Из третьего уравнения получаем для первого случая , а для второго , так что это решение существует лишь при . Таким образом, при имеется одно состояние равновесия, расположенное в начале координат, а при – три состояния равновесия:

, (8.2)

, (8.3)

, (8.4)

которые в дальнейшем будем обозначать соответственно О, О₁ и О₂.

С точки зрения физической интерпретации, в задаче о конвекции первая неподвижная точка отвечает состоянию равновесия и отсутствию конвекционных потоков. Водяное колесо неподвижно. Второе и третье решения соответствуют наличию конвекционного потока – вращению жидкости соответственно против или по часовой стрелке. Водяное колесо вращается в одну или другую сторону с постоянной скоростью. Заметим, что вторая и третья неподвижные точки уравнений Лоренца могут служить примером пары симметричных партнеров – они переходят друг в друга при одновременном изменении знаков x и у.

2. Устойчивость неподвижных точек

Рассмотрим теперь вопрос о том, при каких значениях параметров

найденные неподвижные точки являются устойчивыми или неустойчивыми. Пусть – интересующая неподвижная точка. Будем искать решение уравнений Лоренца в виде

(8.5)

где добавки, отмеченные тильдой, считаются малыми. Пренебрегая квадратами и произведениями малых добавок, из уравнений Лоренца получаем:

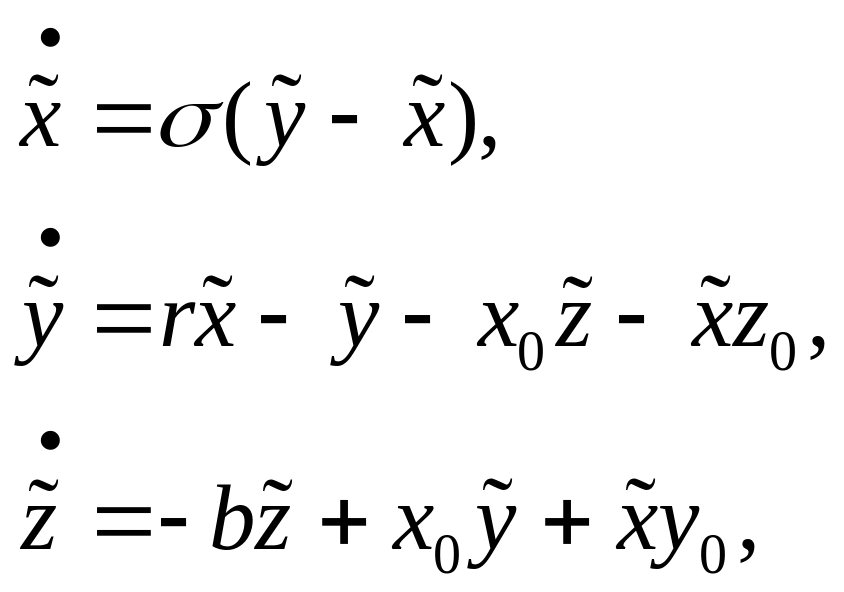(8.6)

где члены нулевого порядка исчезают благодаря условию, что есть неподвижная точка. Как обычно в линейном анализе на устойчивость, предполагаем, что зависимость возмущения от времени экспоненциальная, ~ . Тогда уравнения принимают вид задачи на собственные числа матрицы 3×3:

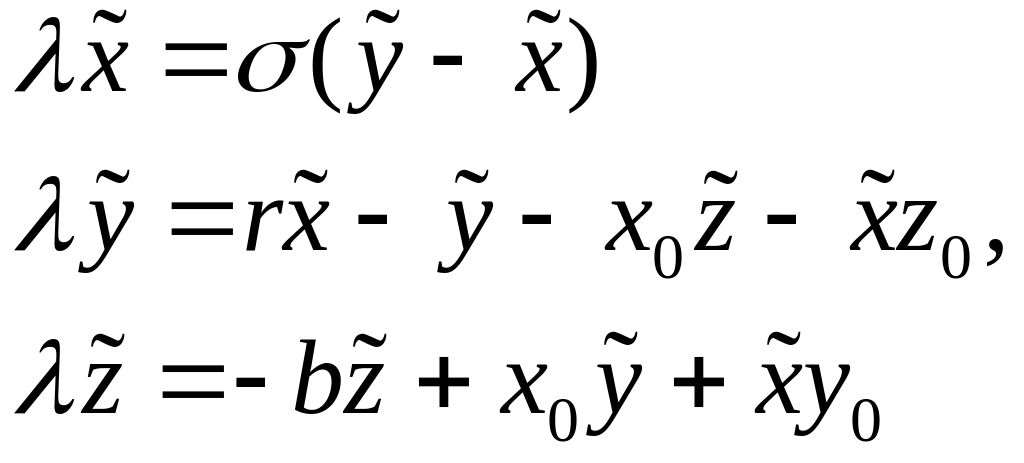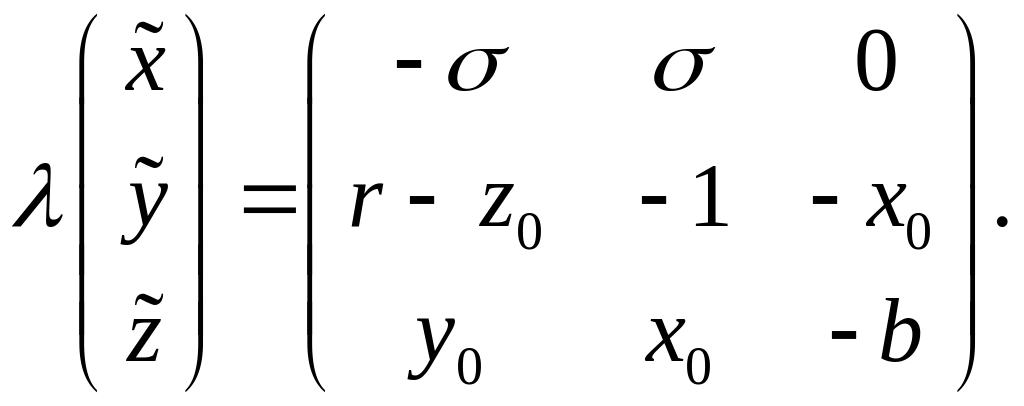или (8.7)

Условием существования нетривиального решения является равенство нулю детерминанта:

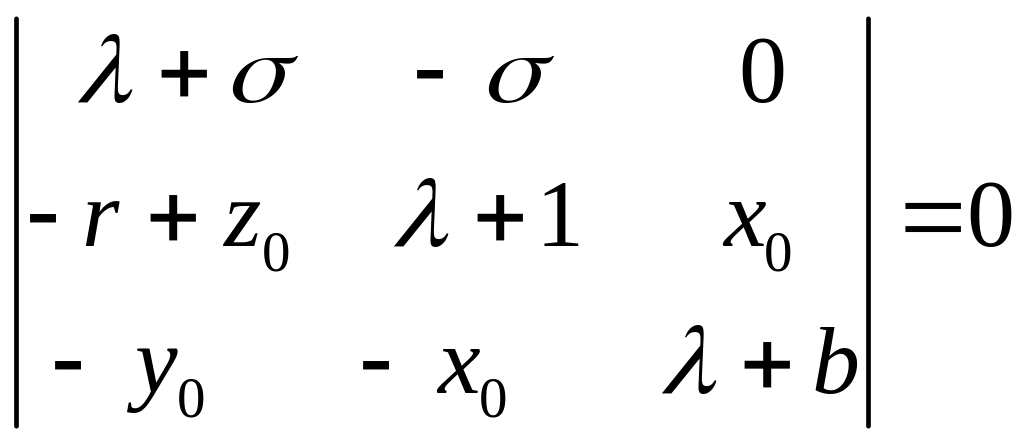(8.8)

или

Для неподвижной точки О, расположенной в начале координат, имеем

или (8.9)

откуда находим три корня:

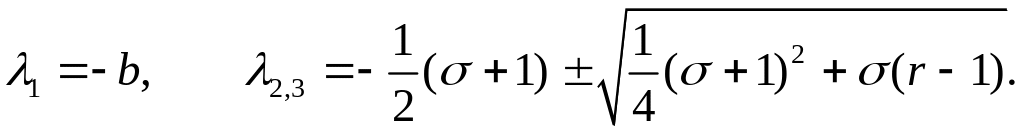(8.10)

Первое собственное число всегда отрицательно. Второе и третье являются отрицательными лишь при r < 1; если же r > 1, одно из них становится положительным. Следовательно, точка О устойчива при r < 1 и неустойчива при r > 1. С точки зрения классификации неподвижных точек, при r < 1 это устойчивый узел, а при r > 1 – седло-узел. Как указывалось при обсуждении смысла параметров в уравнении Лоренца, r есть отношение числа Рэлея к его критическому значению. Мы показали, что стационарное состояние, отвечающее отсутствию конвекционных токов, становится неустойчивым при превышении критического значения r = 1. Тем самым мы воспроизвели результат Рэлея.

Обратимся теперь к точкам О₁ и О₂, которые существуют, как было показано, при r > 1. Подставляя в (8.8)

(8.11)

после алгебраических преобразований получаем кубическое уравнение относительно λ:

(8.12)

Исследование уравнения (8.12) показывает, что при r, лишь немного превышающих 1, все три собственных числа λ отрицательны. Следовательно, неподвижные точки и являются устойчивыми узлами. При увеличении r с некоторого момента они становятся устойчивыми фокусами – одно собственное число действительное и отрицательное, а два других комплексно-сопряженные с отрицательной действительной частью. При дальнейшем увеличении r действительная часть меняет знак, и это момент потери устойчивости состояниями и (в силу симметрии это происходит одновременно).

Найдем порог потери устойчивости для исследуемой неподвижной точки, которому отвечает обращение действительной части корня в ноль. Подставим в формулу (8.12)

(8.13)

и отделим действительные и мнимые части:

(8.14)

Из первого уравнения имеем Подстановка последнего во второе уравнение дает следующее выражения:

Выражая отсюда r , находим порог устойчивости:

(8.15)