7.2. Ограниченность и диссипативность системы Лоренца

Чтобы достигнуть по возможности полного понимания особенностей системы Лоренца, обратимся к рассмотрению тех аспектов динамики, которые можно выявить посредством аналитического исследования.

Симметрия. Прежде всего отметим симметрию уравнений Лоренца – их вид не изменится, если одновременно сменить знак x и у. Это значит, что любое образование в фазовом пространстве либо обладает той же симметрией, т. е. превращается само в себя при замене переменных x → –x, у → –у, либо имеет такое же образование в качестве симметричного партнера. Из рис. 7.2 можно увидеть, что аттрактор Лоренца обладает указанной симметрией.

Ограниченность области, где может располагаться аттрактор. В фазовом пространстве системы Лоренца можно указать такую ограниченную замкнутую область, в которую фазовые траектории могут только входить и никогда ее не покидают. Для упрощения выкладок нам будет удобно здесь использовать следующую форму уравнений Лоренца:

, (7.2)

где .

Умножив первое уравнение на х/σ, второе на у, третье на w и сложив, получим:

(7.3)

Рассмотрим в трехмерном пространстве область Е, заданную неравенством 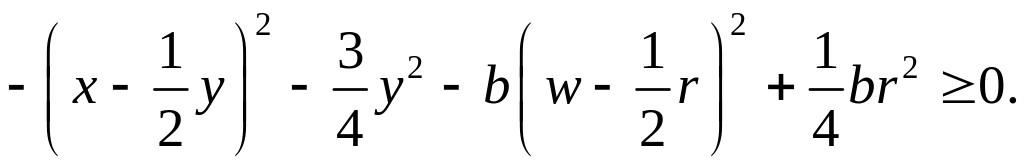Она ограничена поверхностью эллипсоида с центром, смещенным относительно начала координат. Вне этой области правая часть уравнения (7.3) отрицательна. Кроме того, определим семейство эллипсоидов уравнением , где присутствует комбинация, фигурирующая под знаком производной в левой части уравнения (7.3). Выберем значение константы таким большим, чтобы получился эллипсоид S, целиком заключающий в себя область Е. Тогда на поверхности S имеем всюду , т. е. величина убывает с течением времени. Это значит, что все траектории, пересекающие поверхность S, ведут только внутрь ограниченной ею области. Следовательно, каким бы ни был аттрактор уравнений Лоренца, он обязан располагаться внутри S.

Диссипативность системы Лоренца. Рассмотрим векторное поле в трехмерном фазовом пространстве, зависимость трех компонент которого от координат дается правыми частями трех уравнений Лоренца:

. (7.4)

В силу уравнений (7.1) оно имеет смысл поля скоростей в фазовом пространстве: мгновенная скорость движения изображающей точки в момент, когда она имеет координаты , дается вектором L. Вычислим дивергенцию этого поля:

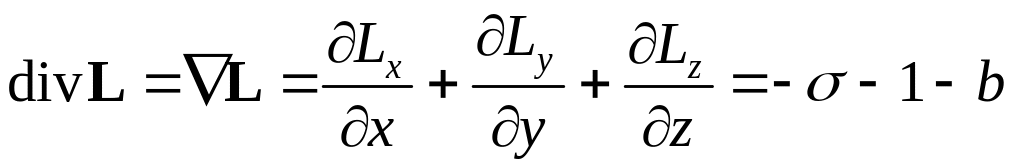. (7.5)

Если параметры σ и b положительны, как это всегда предполагается, то дивергенция постоянна и отрицательна.

Смысл этого результата состоит в следующем. Рассмотрим ансамбль одинаковых систем, каждая из которых описывается уравнениями Лоренца, и пусть они отличаются только начальными условиями. Представим себе, что в начальный момент облако точек, изображающих состояния систем ансамбля в фазовом пространстве, занимает некоторый объем . Тогда в процессе эволюции систем ансамбля во времени объем облака будет уменьшаться по закону , где . С течением времени все они должны сконцентрироваться на некотором множестве нулевого объема – аттракторе. В соответствии с рассуждениями предыдущего пункта, аттрактор обязан располагаться в ограниченной области фазового пространства. (Проведенные рассуждения не исключают возможности существования в упомянутой ограниченной области нескольких аттракторов.)