3. Ошибка центра масс нечеткого множества

Трудность обусловлена тем, что при смещении мало значащих значений в сторону больших значений X (рис. 1.7, при упорядоченном X, в частности при использовании нечетких чисел) наблюдается смещение центра масс нечеткого множества, что приводит к ошибкам интерпретации значения нечеткого множества.

Рис. 1.7. Пример смещения центра масс при учете малозначащих значений

Возможным вариантом устранения погрешностей является использование подходов α-уровневой фильтрации («отсечение» значений с функцией принадлежности меньше α, см. рис. 1.7).

4. Сложности определения нечеткого множества для сложных понятий

Проблема обусловлена возникновением естественных трудностей для специалиста, который должен определить нечеткие оценки для сложного понятия. Данные трудности связаны с трудностями психологического шкалирования.

1.2.2. Операции над нечеткими множествами

В настоящее время разработано достаточно большое количество операций над нечеткими множествами. Ниже в таблице приведены ссылки на основные, наиболее часто используемые операции над нечеткими множествами.

Таблица 1.3

Наиболее часто используемые операции над нечеткими множествами

Наименование операции	Интерпретация	Возможные трудности
1	2	3
Операция объединения	Операция «ИЛИ». Надо чтобы выполнялось хотя бы одно условие	Появление многомодовости получаемых результатов
Операция пересечения	Операция «И». Надо чтобы выполнялись все условия	Уменьшение максимального значения max и появление не нормированных нечетких множеств
Операция Сжатия-растяжения	Уточнение, проявление уровня уверенности в оценках.	Необходимо учитывать нелинейный характер преобразований.
Импликация (эквивалент- ность)	Операция следования или связи на уровне сравнения объектов	При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта
Продолжение табл. 1.3
1	2	3
Операция отрицания	Оценка противоположного события.	Зависит от выбранного генератора отрицания и требует выбора конкретного типа отрицания в соответствии с физикой моделируемого объекта
┴ и Т- нормы и конормы, Средние, OWA-оператор	Могут выполнять различную логику обработки данных в зависимости от выбранных параметров операторов	При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта

Проблема определения операции агрегирования нечетких множеств определяется теми же проблемами, которые отмечены Для получения адекватных оценок необходимо осуществлять процедуры идентификации операций над нечеткими множествами для реальных моделируемых процессов.

Рассмотрим индекс нечеткости или показатель размытости нечетких множеств.

Если объект х обладает свойством R (порождающим нечеткое множество A) лишь в частной мере, т.е. 0<_A(x)<1, то внутренняя неопределенность, двусмысленность объекта х в отношении R проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов, «обладающих свойством R», и классу объектов, «не обладающих свойством R». Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. _A(x) = (x)=0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо _A(x) = 1 и (x) = 0, либо _A(x) = 0 и (x) = 1.

В общем случае показатель размытости нечеткого множества можно определить в виде функционала d(A) со значениями в R (положительная полуось), удовлетворяющего условиям:

1. d(A) = 0 тогда и только тогда, когда А - обычное множество;

2. d(A) максимально тогда и только тогда, когда _A(x) = 0.5 для всех xE.

3. d(A)d(B), если A является заострением B, т.е.

4. _A(x)_B(x) при _B(x) < 0,5;

5. _A(x)_B(x) при _B(x) > 0,5;

6. _A(x)- любое при _B(x) = 0,5.

7. d(A) = d( ) - симметричность по отношению к 0,5.

8. d(AB)+d(AB) = d(A)+d(B).

Обычное множество, ближайшее к нечеткому

Пусть A - нечеткое множество. Возникает вопрос, какое множество AE является ближайшим к A, т.е. находится на наименьшем евклидовом расстоянии от нечеткого множества A. Таким подмножеством, обозначаемым A, является подмножеством с характеристической функцией:

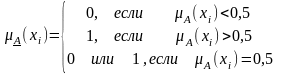(1.6)

Обычно принимают µ_A(x_i) = 0, если µ_A(x_i) = 0,5.

Используя понятие обычного множества, ближайшего к нечеткому, введем следующие индексы нечеткости нечеткого множества А.

Линейный индекс нечеткости:

Здесь p(A, A) - линейное (хеммингово) расстояние, множитель обеспечивает выполнение условия 0<d(A)<1.

Квадратичный индекс нечеткости

Здесь ε(A, A) - квадратичное (евклидово) расстояние.

Замечания.

1. Мы ввели линейный и квадратичный индексы нечеткости, используя понятие расстояния и понятие обычного множества, ближайшего к нечеткому. Эти же индексы можно определить, используя операцию дополнения, следующим образом:

- линейный индекс,

- квадратичный индекс.

3. Отметим следующие свойства, связанные с ближайшим обычным множеством:

А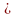 В=А В, А В=А В;

а также x E:| µ_A(x_i)- µ_A(x_i)|=, откуда для линейного индекса нечеткости имеем:

,

т.е. в этом представлении становится очевидным, что d(A)=d( ).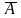

3. Нечеткое множество с функцией принадлежности иногда называют векторным индикатором нечеткости.