3.1. Общие понятия теории систем
3.1.1. Общая системы, глобальные состояния и глобальная реакция системы
При построении теории общих систем мы будем исходить из следующих определений.
(Общей) системой называется отношение на непустых (абстрактных) множествах
(3.1)
где символ декартова произведения, а I – множество индексов. Множество Vi мы будем называть объектом системы. Если множество I конечно, то (3.1) можно переписать в виде
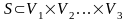(3.2)
Пусть
и
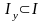образуют разбиение множества I,
т. е. пусть
и
..
Множество
будем называть входным объектом, а
множество-
выходным объектом системы. Тогда система
S
определяется отношением
(3.3)
(такую систему мы будем называть системой «вход — выход» )).
Если S является функцией:
(3.4)
то соответствующая система будет называться функциональной.
Заметим, что в формулах (3.2) и (3.3) используется один и тот же символ S, хотя, строго говоря, элементами отношения в (3.2) являются n-ки, в то время как в (3.3) — это пары. Конкретный характер интерпретации S всегда будет ясен из контекста, в котором этот символ используется. Аналогичные замечания можно высказать и по поводу использования одинакового символа S в (3.3) и в (3.4).
Для удобства
обозначений мы примем также следующее
соглашение: скобки в
выражении
будут означать, что
функция F
является всего лишь
частичной, т.е. что она не обязательно
определена для любого элемента множества
А. Область пределения функции F
(или просто область)
будет обозначаться через
,
а область ее значений(или ее кообласть)
через
.
Аналогично будут
обозначаться и область, и кообласть
отношения
:
,
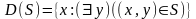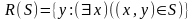
Для упрощения обозначений в дальнейшем всегда будет предполагаться, что D(S) = X , если только не оговорено противное.
Для данной общей
системы S
пусть С произвольное множество, а
функция
такова, что:
Тогда С называется множеством или объектом глобальных состояний системы, а его элементы – просто глобальными состояниями системы, функция же R называется глобальной реакцией (системы).
Теорема 1.1. Каждой системе соответствует некоторая глобальная реакция, и эта функция R не является частичной, т. е.
3.1.2. Абстрактные линейные системы
Хотя многие понятия теории систем и можно определить, опираясь исключительно па понятие общей системы, получение содержательных математических результатов становится возможным только после введения дополнительных структур. Чтобы избежать чрезмерного количества определений, мы будем, как правило, вводить конкретные понятия па том же уровне общности, на котором для них можно получить нетривиальные математические результаты. Например, понятие динамической системы будет введено лишь в контексте временных систем. Тем не менее понятие линейности оказывается полезным уже на любом уровне общности. Поэтому мы определим это понятие сейчас и будем пользоваться им как стандартным.
Пусть — А некоторое поле, X и Y – линейные алгебры над A, S – отношение, , причем S непусто. Пусть, кроме того,
,
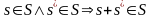где + обозначает (внутреннюю) операцию сложения в X х Y ,а через as обозначен результат (внешней) операции умножения на скаляр. Тогда S называется (абстрактной) полной линейной системой.
Пусть X и Y – линейные алгебры над одним и тем же полем А. Система является линейной в том и только в том случае, когда найдется такая глобальная реакция , что:
1) С есть линейная алгебра над А;
2) Существует
пара таких линейных отображений
и
,
что для всех
.
Пусть - линейная система, a R – отображение, . Отображение называется линейной глобальной реакцией системы тогда и только тогда, когда
1) R согласуется с S, т. е.
2) С является линейной алгеброй над полем А скаляров линейных алгебр X и Y.
3) существуют два таких линейных отображения и , что для любых
В этом случае С называют линейным объектом глобальных состояний, отображение – глобальной реакцией на состояние, a – глобальной реакцией на вход.