1.6. Расчет характеристик поля излучения в дальней зоне

Рассмотрим излучающую систему антенны (рис. 1.4) в виде совокупности N одинаково ориентированных в пространстве дискретных излучателей — источников электрического тока с комплексными амплитудами . Пусть каждый излучатель создает в дальней зоне электрическое поле с напряженностью . Тогда, основываясь на принципе суперпозиции, для определения любой компоненты результирующего комплексного вектора напряженности электрического поля излучения в дальней зоне следует учесть, что , и затем использовать выражение вида [2, 5]

, (1.31)

где А — амплитудный множитель, зависящий от типа излучателя; — комплексная характеристика направленности излучателя; — амплитудная, а — фазовая характеристика направленности.

Такого рода излучающие системы из одинаковых элементов называются антенными решетками и широко применяются в антенной технике для получения остронаправленного излучения. Из выражения (1.31) следует, что характеристика направленности всей АР для любой компоненты поля может быть представлена в виде произведения [2, 5]

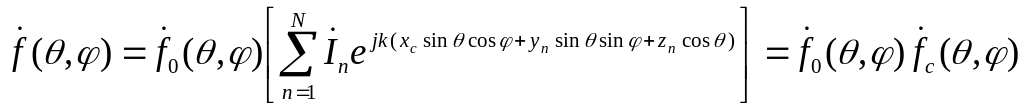, ( 1.32)

где — комплексная характеристика направленности одиночного элемента; — комплексная функция, называемая множителем системы (решетки).

Множитель системы любой АР из элементов с одинаковым расположением в пространстве определяется следующими факторами:

- амплитудами токов в элементах;

- фазами токов в элементах и фазовым сдвигом создаваемых ими полей, обусловленным разностью расстояний от каждого элемента до точки наблюдения по сравнению с расстоянием до нее от начала общей системы координат.

Для выяснения смысла множителя системы рассмотрим АР, в которой реальные излучающие элементы заменены на изотропные (ненаправленные) элементы, имеющие . Из (1.31) следует, что множитель системы описывает характеристику направленности АР из изотропных элементов, возбуждаемых такими же токами , что и элементы реальной АР. Анализ выражения (1.32) позволяет сформулировать исключительно важное правило, получившее в теории и технике антенн название теоремы перемножения характеристик (диаграмм) направленности [2, 3, 5]: характеристика направленности системы из реальных одинаковых излучающих элементов представляет собой произведение характеристики направленности одного элемента и характеристики направленности такой же точно системы, но состоящей из изотропных элементов, возбуждаемых токами с такими же амплитудами и фазами, что и реальные элементы. Важно, что множитель системы не зависит от типа излучающих элементов и одинаков для любой компоненты ЭМП излучения. Поэтому поляризация излучения АР остается такой же, как и поляризация отдельного элемента.

Все сказанное выше остается в силе и в случае излучающих систем с непрерывным распределением источников тока, если излучатели (элементы тока) расположены на одной прямой линии или на плоской поверхности.

Так, для линейной антенны длиной L с известным непрерывным распределением тока вдоль оси множитель системы определяется выражением [2]

. (1.33)

Для апертурной антенны, плоскость раскрыва которой проходит через начало координат z=0, с известным амплитудно-фазовым распределением (АФР) поля в раскрыве [2]

,

где — амплитуда напряженности возбуждающего электрического поля (поляризованного вдоль оси OY) в начале координат, при равенстве волнового сопротивления среды W и отношения амплитуд поперечных компонент ЭМП в раскрыве [2, 5], множитель системы для раскрыва площадью S определяется выражением [2, 5]

. (1.34)