9. Апертурные антенны

К апертурным относят антенны, имеющие некоторую поверхность (апертуру, раскрыв) S, формирующую направленное излучение: волноводные излучатели, рупорные, зеркальные и линзовые антенны [2, 5]. В апертурных антеннах реализуется параллельное возбуждение элементов излучающей поверхности, благодаря чему форма и параметры ДН остаются практически неизменными в довольно широкой полосе рабочих частот. Максимальный КНД апертурных антенн определяется выражением

, (9.1)

где S — геометрическая площадь раскрыва; ν — КИП, зависящий от амплитудного и фазового распределения напряженности электрического поля, возбуждающего раскрыв; λ₀ — длина волны. Из (9.1) следует, что КНД существенно зависит от отношения и при больших размерах раскрыва может достигать очень высоких значений порядка 10⁴—10⁵. КУ апертурных антенн определяется общим выражением , где η — КПД антенны.

9.1. Волноводные излучатели

В качестве слабонаправленных антенн (в том числе, облучателей зеркальных и линзовых антенн), а также элементов антенных решеток СВЧ и КВЧ диапазонов широко используются излучатели в виде открытых концов металлических волноводов, обычно прямоугольного или круглого сечения [2,5]. ЭМВ, распространяющаяся по волноводу и достигающая его открытого конца, частично отражается в силу появления неоднородности — отличия характеристического сопротивления рабочей волны в волноводе от волнового сопротивления окружающего пространства, а частично излучается (рис. 9.1) . В области открытого конца в силу нарушения регулярности структуры возникают волны высших типов.

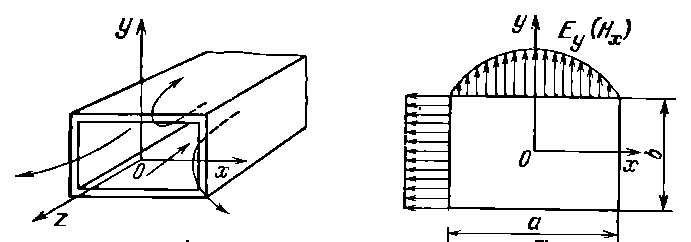
Рис. 9.1. Излучатель в виде открытого конца прямоугольного металлического волновода с волной Н₁₀

Учет всех названных факторов очень усложняет задачу определения поля излучения открытого конца волновода и ее строгое математическое решение сопряжено с большими трудностями. Согласно принципу Гюйгенса—Кирхгофа, применительно к волноводному излучателю можно рассмотреть замкнутую поверхность, внутри которой находятся источники ЭМП — токи, протекающие как по внутренним, так и по внешним стенками волновода. Эта поверхность выбирается так, что она совпадает с поверхностью открытого конца волновода и с наружными поверхностями его стенок. Упрощенный анализ излучения волновода обычно проводят с использованием принципа эквивалентности с учетом граничных условий для тангенциальных компонент полей ; причем на внешней поверхности волновода поверхностные токи и принимаются равными нулю. Соответственно, в случае прямоугольного волновода, возбуждаемого основной волной типа , считают, что ЭМП в раскрыве определяется падающей и отраженной волнами и представлено следующими взаимно перпендикулярными компонентами напряженностей и [10]:

, (9.2)

, (9.3)

где — напряженность электрического поля в середине раскрыва волновода; — длина волны в свободном пространстве; 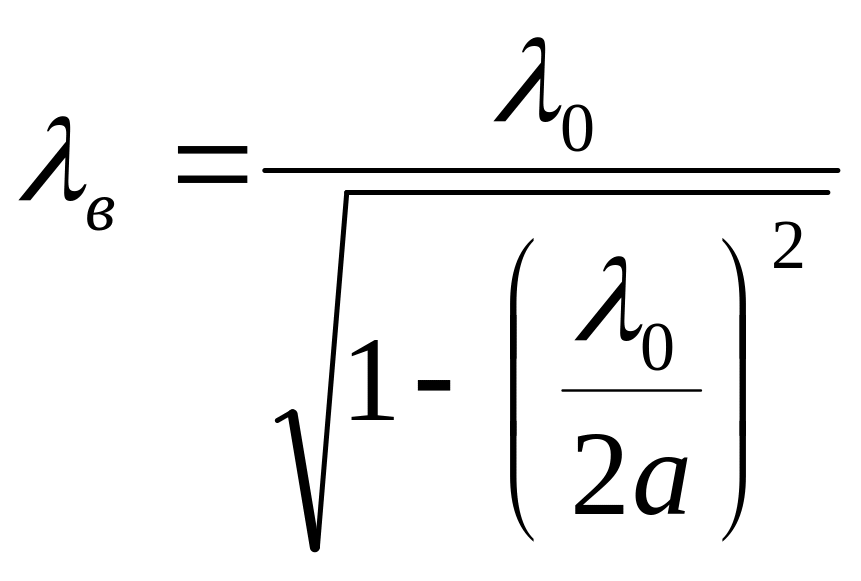— длина волны в волноводе; — комплексный коэффициент отражения волны от открытого конца; Ом — волновое сопротивление среды (свободного пространства); a и b — внутренние размеры широкой и узкой стенок.

Выражения для комплексных амплитуд вектора Е ЭМП излучения в дальней зоне, полученные в соответствии с теорией излучения возбужденных поверхностей, для главных плоскостей Е (yoz) и Н (xoz) имеют вид [10]

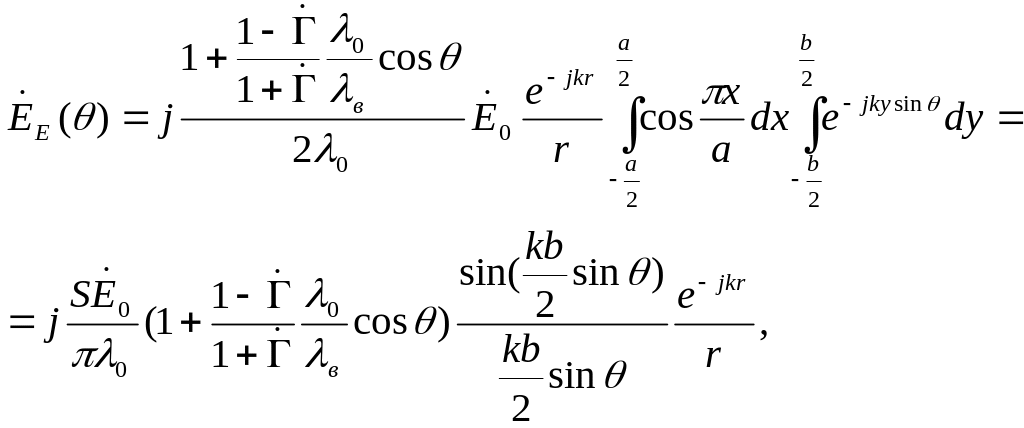(9.4)

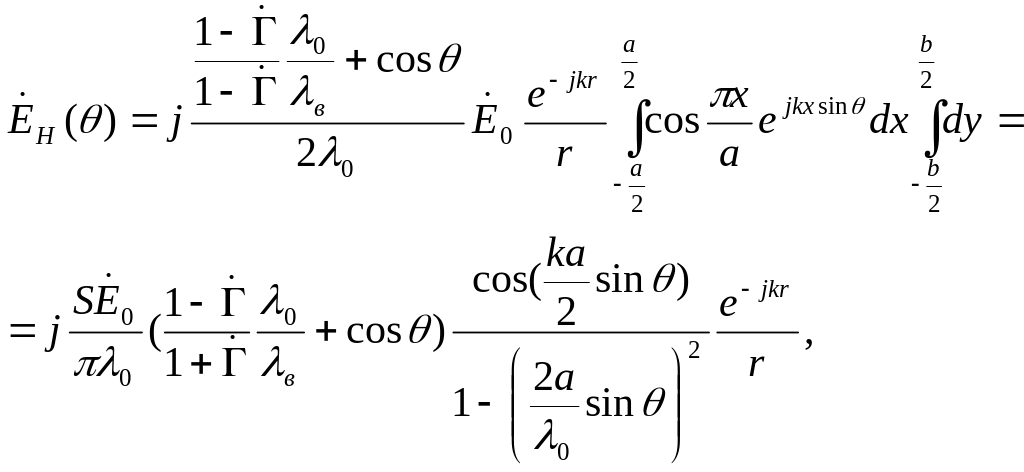(9.5)

где — площадь раскрыва; угол θ отсчитывается от нормали к плоскости раскрыва (оси z).

Обозначим в выражениях (9.4) и (9.5) отношение и запишем формулы для ненормированных ДН по напряженности поля для плоскостей Е (при φ=π/2) и Н (φ=0) :

, (9.6)

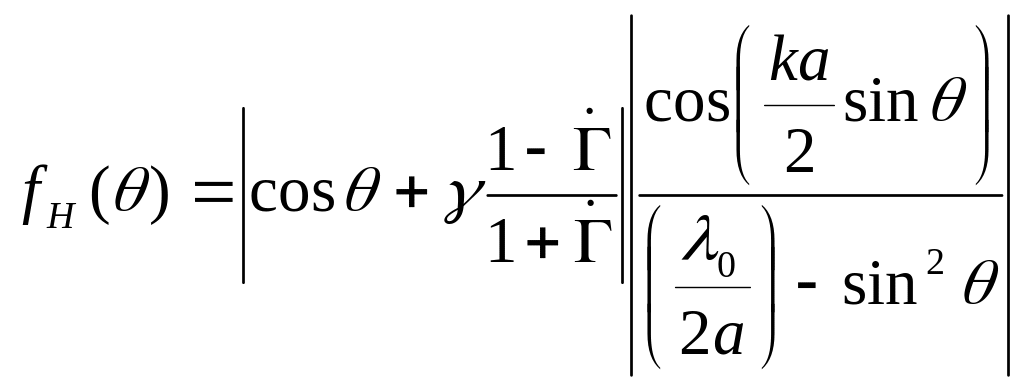. (9.7)

Заметим, что если не учитывать отражения от конца волновода ( ) и считать, что длина волны в раскрыве равна длине волны в свободном пространстве, т.е. принять γ=1, то из формул (9.6) и (9.7) легко получить формулы для нормированных ДН плоского раскрыва, возбуждаемого плоской поперечной ЭМВ, аналогичные полученным в разделе 4:

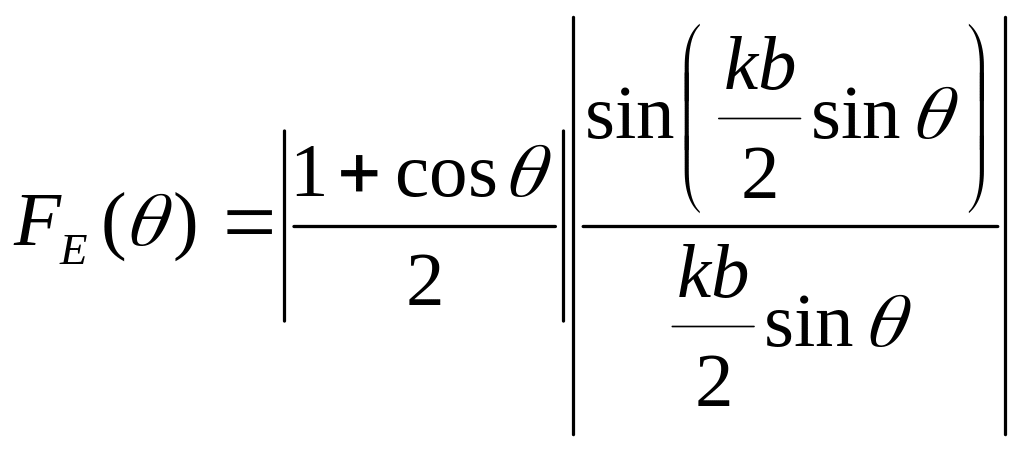, (9.8)

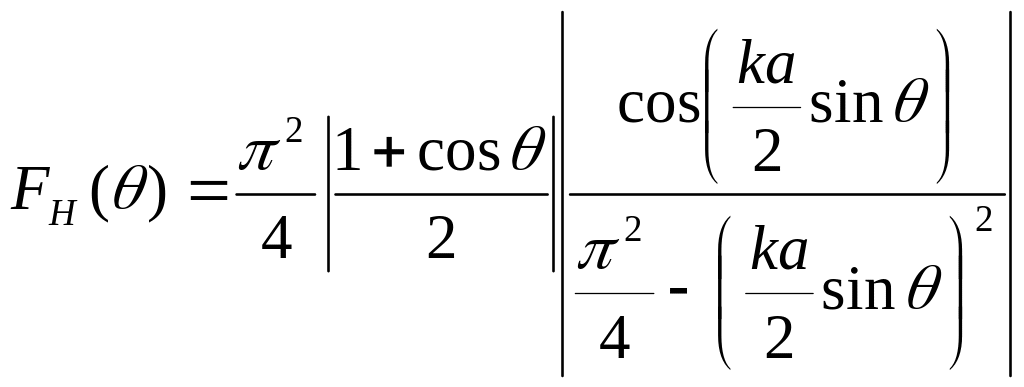. (9.9)

КНД открытого конца волновода без учета отражений определяется приближенным выражением [10]

. (9.10)

Размеры поперечного сечения стандартного волновода невелики, и поэтому ширина ДН в обеих плоскостях велика ( , ).

Соответственно, КНД открытого конца прямоугольного волновода составляет около 4 дБ, модуль коэффициента отражения ≈0,3; КНД волновода со стандартным фланцем составляет около 6 дБ, модуль коэффициента отражения ≈0,25 [45], т.е., открытый конец прямоугольного волновода плохо согласован со свободным пространством.

Надо отметить, что приведенные выше выражения дают лишь приближенные результаты и удовлетворительно описывают ДН только в переднем полупространстве. Это связано с тем, что, в частности, при их выводе не учитывались токи на внешних поверхностях волновода.

Несколько лучшими характеристиками обладает излучатель в виде открытого конца круглого металлического волновода с рабочей волной основного типа Н₁₁ [10]. Так, для волновода с радиусом а при рабочей длине волны значительно короче критической ширина ДН по половинной мощности в Е- и Н-плоскостях определяется выражениями [10]

, , (9.11)

КНД —

. (9.12)