Не зависит от угла , то есть представляет собой окружность.

Перепишем (5.14) в виде

и в соответствии с (2.4) получим выражение для нормированной ДН СЭВ по напряженности электрического поля:

,

. (5.15)

В (5.15) первый сомножитель описывает ДН элементарного электрического вибратора — диполя Герца, второй — ДН множителя системы [1, 10, 11].

Диаграммы направленности сэв

Как видно из формулы (5.11), направленные свойства СЭВ при синусоидальном распространении тока определяются только электрической длиной плеча вибратора, т.е. отношением . В случае, когда и, следовательно, L=λ₀/2 (полуволновой вибратор) выражение (5.10) примет вид

, (5.16)

Нормированная дн по напряженности поля

. (5.17)

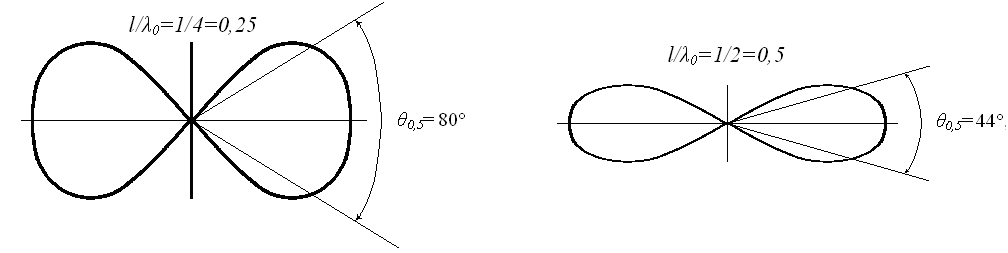
а б

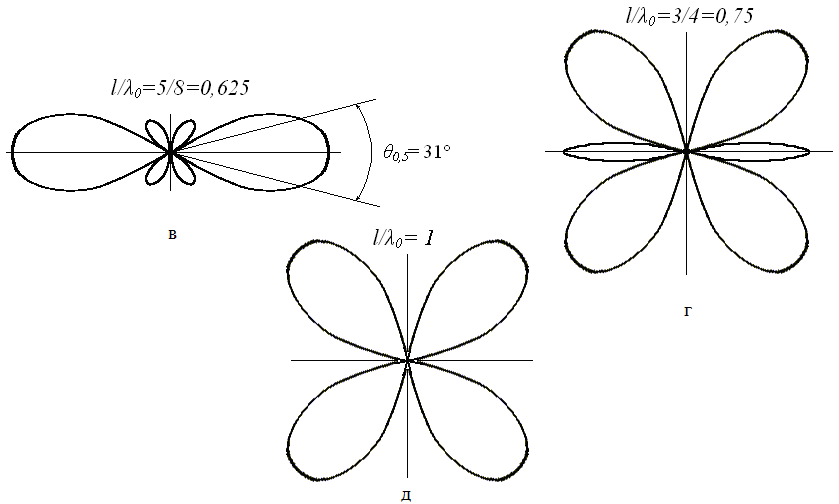
Рис. 5.4. Нормированные ДН СЭВ в плоскости E для различных отношений

Анализ формулы (5.15) и рассмотрение ДН СЭВ (рис. 5.4) показывают, что при любой величине отношения l/λ₀ симметричный вибратор не излучает вдоль своей оси. Если длина плеча симметричного вибратора l 0,5λ₀, то в направлении, перпендикулярном его оси (θ=90°, θ=270°), т.е. в экватори­альной плоскости, напряженности полей всех ЭЭВ максимальны, синфазны и складываются арифметически. Поэтому напряженность поля СЭВ в данном направле­нии является максимальной. ДН при l/λ₀ 0,5 со­стоит из двух (главных) лепестков (рис. 5.4, а, б). Увеличение длины виб­ратора до l=0,5λ₀ сопровождается ростом излучения в направлении, перпен­дикулярном оси вибратора (главное направление излучения), за счет уменьшения излучения в других направлениях. При этом диаграмма направленности становится уже. При увеличении l/λ₀ до 5/8=0,625 излучение в главном направлении продолжает усиливаться, но ДН проходит через нуль не только при θ=0° и θ=180°, но и при неко­торых других значениях угла θ. Главные лепестки ДН становятся уже, но появляются боковые лепестки (рис. 5.4, в). При дальнейшем увеличе­нии l/λ₀ излучение в главном направлении ослабляется и возрастают боко­вые лепестки. Ослабление излучения в главном направлении объясняется тем, что результирующий сдвиг фаз полей, излучаемых ЭЭВ в данном направлении, определяется пространственным сдви­гом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/λ₀ >0,5 на вибраторе появляются участки с противофазными токами (рис. 5.2), длина которых растет по мере увеличения l/λ₀. Поэтому хотя в главном направлении пространственные сдвиги фаз равны нулю, по­ля излучений отдельных элементов вибратора складываются несинфазно, т.е. геометрически. Рост l/λ₀ сопровождается также ростом боковых лепестков. Уже при l/λ₀=0,75 напряженность поля в на­правлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис. 5.4, г). При l/λ₀=1 (или при l/λ₀ = n, где n = 1, 2, …) излу­чение в главном направлении отсутствует (рис. 5.4, д), так как противофазные участ­ки плеч вибратора имеют одинаковую длину.

Ширина ДН ЭЭВ (диполя Герца) по половинной мощности излучения θ_0,5= 90°. Полуволновый СЭВ имеет ширину ДН θ_0,5= 80°, волновый СЭВ — θ_0,5= 44°, а СЭВ с l/ =0,625 имеет θ_0,5= 31°. Последний вибратор обладает наи­лучшими направленными свойствами, так как при дальнейшем увеличении l/λ₀, сильно возрастают боковые лепестки, хотя главный лепесток ДН становится уже. На практике применяются СЭВ, у которых l/λ₀ 0,7. Фаза напряженности поля, создаваемого симметричным вибратором в соответствии с выражением (5.10), в пределах одного лепестка диаграммы направленности не зависит от координатного угла θ. Она изменяется скачком на противоположную при переходе напряжённости поля через нуль. СЭВ излучает сферические волны, о чем свидетельствует множитель exp(−ikr)/r. Эти волны как бы исходят из од­ной точки, совпадающей с центром вибратора.

5.3. Мощность и сопротивление излучения, КНД и действующая длина симметричного электрического вибратора

Для определения мощности излучения СЭВ воспользуемся методом вектора Пойнтинга. Окружим СЭВ сферой радиусом и совместим ее центр с центром вибратора (рис. 5.5).

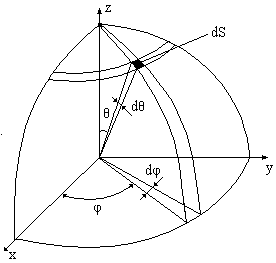
Рис. 5.5. К расчету мощности излучения вибратора

Мощность излучения СЭВ, проходящая через элементарную площадку dS на поверхности сферы, определяется выражением

, . (5.16)

Учитывая, что и

,

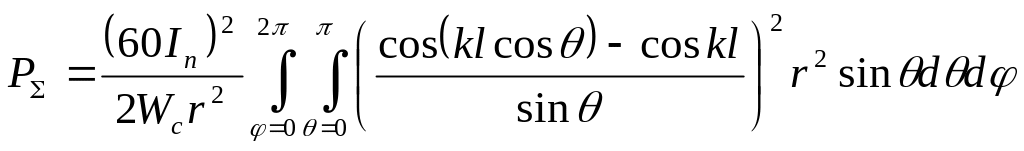. (5.17)

Для СЭВ, находящегося в свободном пространстве, волновое сопротивление и

.

Выразим мощность излучения СЭВ через его сопротивление излучения:

, тогда

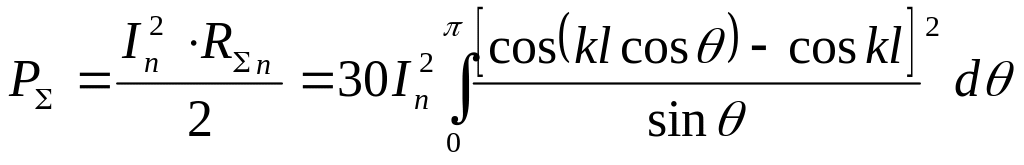. (5.18)

Сопротивление излучения, отнесенное к току в пучности, определяется выражением [10, 11]:

. (5.19)

После интегрирования получается формула, полученная Баллантайном [10, 11]:

, (5.20)

где — постоянная Эйлера; — интегральный синус, — интегральный косинус [11]. График зависимости сопротивления излучения тонкого СЭВ, отнесенного к току в пучности, от электричской длины плеча l/λ₀, рассчитанный по (5.20), показан на рис. 5.6:

Рис. 5.6. Зависимость сопротивления излучения тонкого СЭВ, отнесенного к току в пучности, от электрической длины плеча l/λ₀

Осциллирующий характер зависимости (l/λ₀) при l/λ₀>0,5 объясняется появлением на плечах СЭВ участков с противофазными токами.

Соответственно, переходя к сопротивлению излучения, отнесенному к току в точках питания, можно получить выражение

. (5.21)

Для коротких СЭВ при l/λ₀<<1 [10, 11]

. (5.22)

Сопротивление излучения полуволнового СЭВ =73,1 Ом.

КНД СЭВ можно определить, используя общее выражение (2.8) и формулу для нормированной ДН по напряженности поля (5.11) с последующим численным интегрированием. С другой стороны, используя определение КНД антенны (2.4)

, где ,

и выражение для напряженности электрического поля (5.11), можно получить удобную расчетную формулу для КНД

, (5.23)

для СЭВ в свободном пространстве Ом.

График зависимости КНД СЭВ от электрической длины плеча l/λ₀ приведен на рис. 5.7 [10].

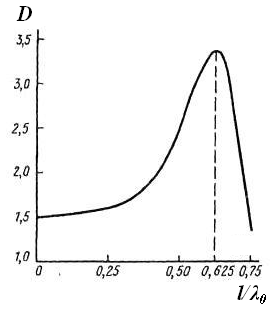
Рис. 5.7. Зависимость КНД СЭВ в направлении θ=90˚ от электрической длины плеча l/λ₀

Для практических целей следует обратить внимание на следующие характерные значения КНД: для ЭЭВ (l/λ₀→0) D=1,5; для полуволнового СЭВ D=1,64; для СЭВ с l/λ₀=0,625 КНД достигает наибольшего значения D=3,36 и затем по мере увеличения l/λ₀ монотонно снижается, что обусловлено уменьшением уровня ГЛ и увеличением уровня БЛ ДН.

Действующая длина СЭВ

Определим действующую длину (высоту) вибратора для любых направлений в экваториальной плоскости, то есть θ=90˚ . Воспользуемся формулой [10]

. (5.24)

Подставив в (5.24) , получим

.

Учитывая, что при амплитуда тока в точках питания

,

получаем выражение для действующей длины, отнесенной к :

. (5.25)

Если отнести к получаем [10, 11]

. (5.26)

Для полуволнового вибратора [10, 11]

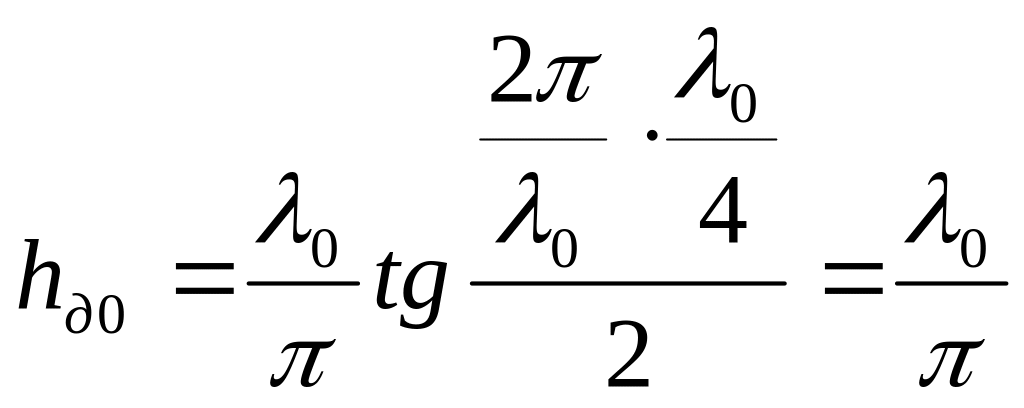. (5.27)

Для коротких вибраторов

,

т.е. действующая длина равна половине геометрической длины.

5.4. Входное сопротивление симметричного электрического вибратора

В режиме излучения СЭВ является нагрузкой источника (генератора) электромагнитных колебаний. При этом подводимая к СЭВ мощность преобразуется в мощность излучения, рассеивается в самом вибраторе (расходуется на нагрева­ние проводников, потери в изоляторах и в окружающих предметах) и затрачивается на создание реактивного ЭМП, связанного с вибратором. Мощности излучения соответствует активное сопротивление излучения , мощности потерь — активное сопротивление потерь , а реактивной мощности — реактивное сопро­тивление . Таким образом, подключенный к СЭВ источник нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и равно отношению комплексных амплитуд напряжения и тока в точках питания вибратора (рис. 5.8):

.

Как показано в разделе 2, для определения можно воспользоваться, например, методом наведенных ЭДС и методом эквивалентной схемы.

В [2, 5] показано, что в случае бесконечно тонкого СЭВ малой длины (L=2l<λ₀/4) в предположении отсутствия в нем тепловых потерь ( ) и синусоидального распределения тока входное сопротивление СЭВ в точках питания

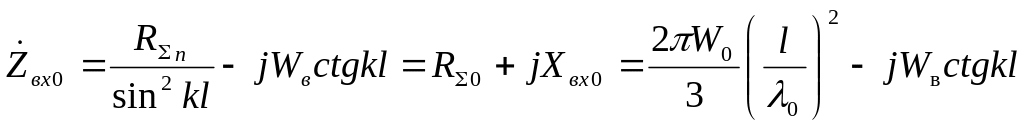, (5.28)

где — волновое сопротивление свободного пространства;

W_в=120(ln l/a-1) — волновое сопротивление СЭВ, рассчитанное методом Хоу (5.5); соответственно,

. (5.29)

Очевидно, что при питании СЭВ в пучности напряжения ( =0,5; 1,0; …) стремится к бесконечности, поскольку при этом ток в точках питания оказывается равным нулю. На самом деле ток в узлах никогда не равен нулю и входное сопротивление хотя и становится высоким, но остается конечным. Поэтому формулы (5.28) и (5.29) имеют ограниченное применение.

Для получения более универсального выражения для входного сопротивления воспользуемся вторым методом, согласно которому СЭВ (вообще говоря, и любая другая антенна) заменяется некоторой эквивалентной электрической цепью с распределенными или сосредоточенными параметрами. Значения этих параметров подбираются так, чтобы входное сопротивление цепи наиболее точно аппроксимировало входное сопротивление антенны в заданной полосе частот и передавало его зависимость от размеров антенны. В случае СЭВ в инженерной практике хорошо зарекомендовала себя схема замещения в виде отрезка разомкнутой на конце двухпроводной ЛП с потерями (рис. 5.8) [5].

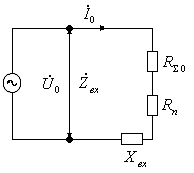
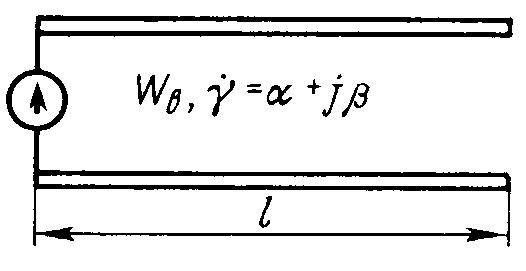
Рис. 5.8. Схема замещения вибратора и эквивалентный отрезок разомкнутой линии передачи

Условия эквивалентности схемы анализируемому СЭВ состоят в следующем [5]:

1. длина отрезка ЛП полагается равной длине плеча СЭВ;

2. полная мощность потерь в схеме замещения и мощность излучения СЭВ на всех частотах равны;

3. волновое сопротивление эквивалентной линии равно волновому сопротивлению СЭВ, определенному по методу Хоу;

4. коэффициент фазы тока 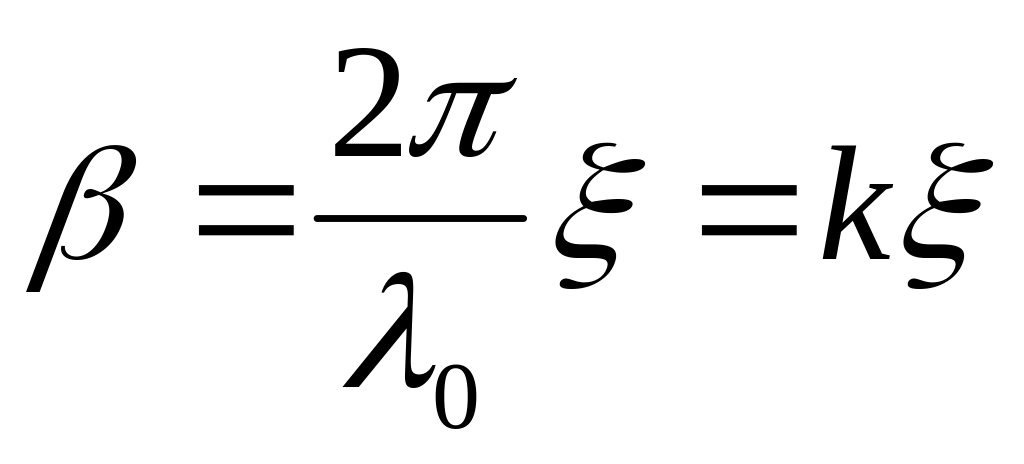, 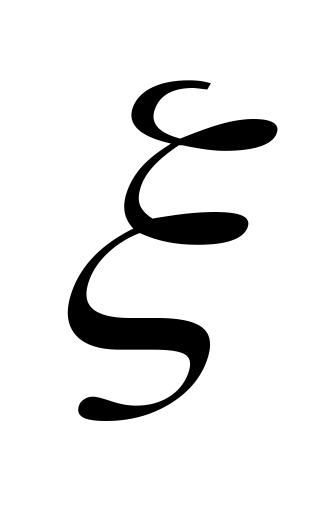— поправочный множитель, учитывающий емкости торцов СЭВ конечной толщины и то, что на самом деле СЭВ не является однородной линией с постоянными погонными параметрами.

Для составленной эквивалентной схемы основными параметрами являются: длина отрезка l, комплексное волновое сопротивление линии и комплексная постоянная распространения волны в линии , — коэффициент затухания, β — коэффициент фазы; тогда

. (5.30)

График зависимости , полученный экспериментальным путем и приведенный в [5], представлен на рис. 5.9.

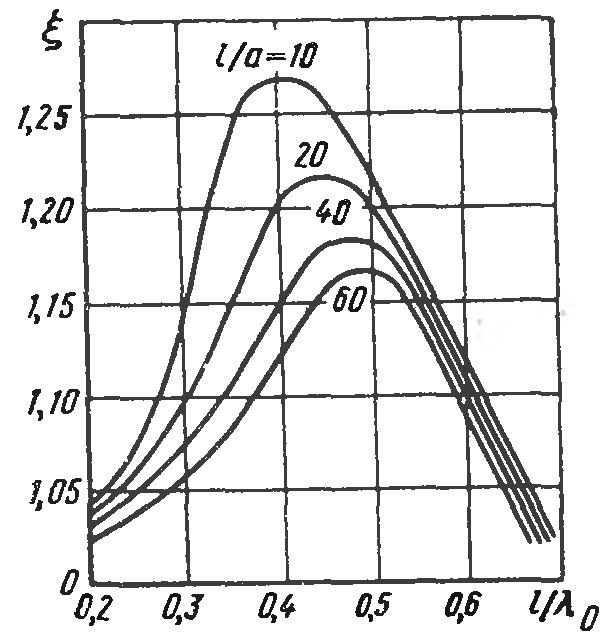
Рис. 5.9. Зависимость поправочного коэффициента от электрической длины плеча вибратора

Распределение тока в таком отрезке описывается законом гиперболического синуса ; соответственно, в узлах ток не обращается в нуль. Для ЛП с потерями [2, 5]

, (5.31)

где R₁ — погонное сопротивление каждого проводника ЛП; L₁, C₁ — погонные индуктивность и емкость ЛП; W_в — волновое сопротивление ЛП без учета потерь; — коэффициент ослабления в линии. Теперь под R₁ будем подразумевать распределенное по длине СЭВ сопротивление излучения, которое в предположении синусоидального закона распределения тока в СЭВ определяется выражением [5]:

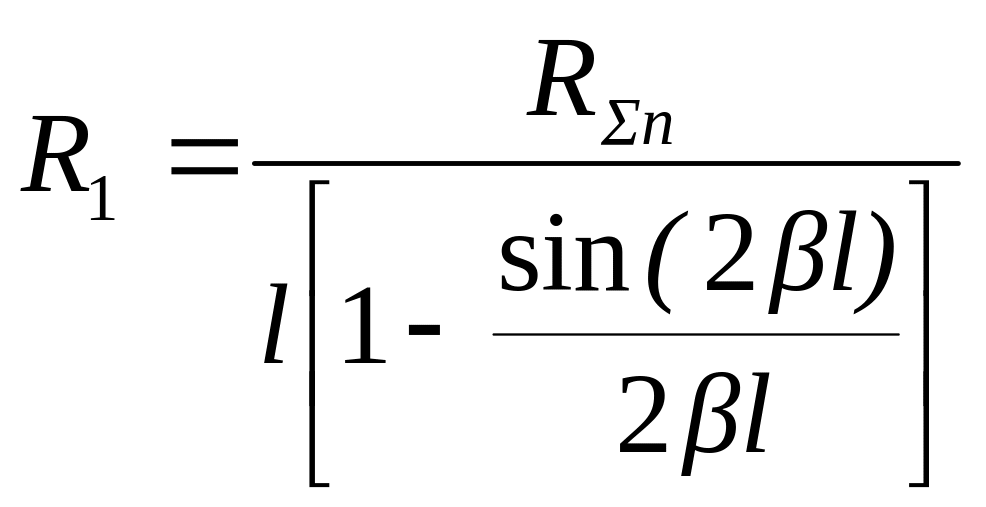, (5.32)

под волновым сопротивлением линии без потерь — волновое сопротивление СЭВ :

.

Учитывая связь постоянной распространения с погонными параметрами ЛП , выражение (5.31) можно преобразовать к виду

(5.33)

и получить приближенное расчетное выражение для входного сопротивления СЭВ [2, 5]:

, (5.34)

где 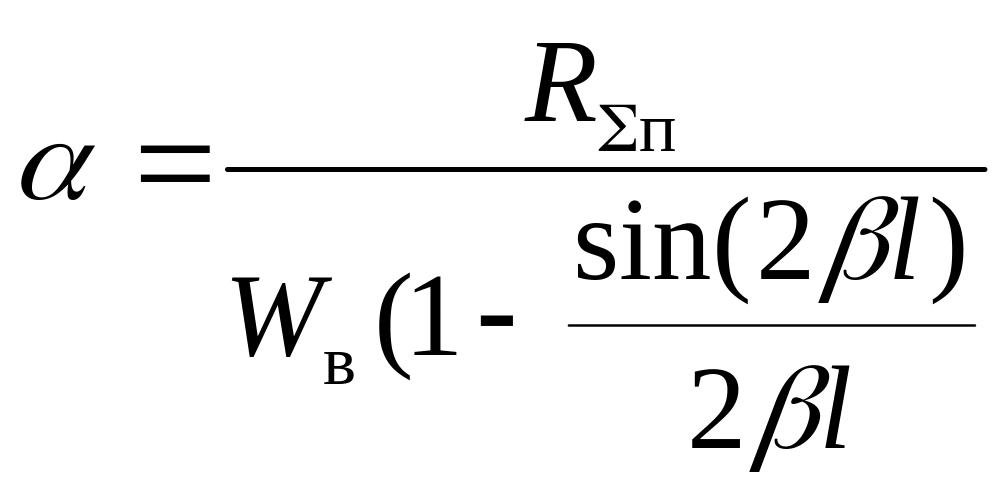, . (5.35)

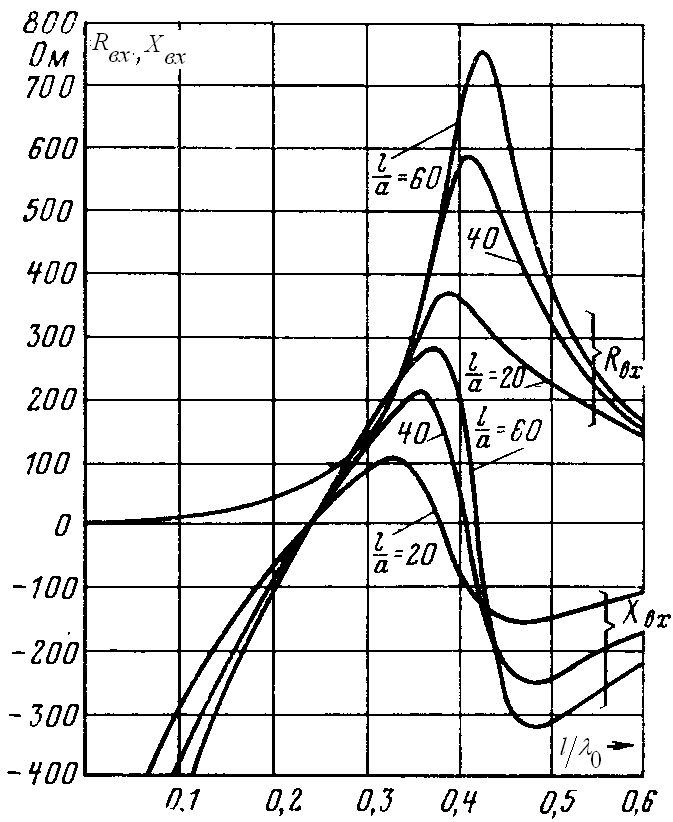
Рис. 5.10. Зависимости активной и реактивной компонент входного сопротивления СЭВ от электрической длины плеча

На рис. 5.10 [5] приведены графики активной и реактивной компонент входного сопротивления СЭВ от электрической длины плеча , построенные для различных отношений длины и радиуса плеча СЭВ . Из представленных зависимостей следует, что:

1) при увеличении относительной длины плеча СЭВ от 0 до 0,6 входное сопротивление характеризуется двумя резонансами. Первый (последовательный) резонанс имеет место в окрестности ; второй (параллельный) — при немного менее 0,5; при этом реактивная компонента обращается в нуль. Соответственно, при питании в пучности тока (при первом резонансе) СЭВ подобен последовательному колебательному контуру, при питании в узле тока (при втором резонансе) — параллельному. Точное значение резонансных длин плеч несколько меньше, чем 0,25λ₀ и 0,5λ₀, что объясняется отличием коэффициента фазы тока β в вибраторе конечной толщины от k. При (полуволновый СЭВ) и бесконечно малом радиусе плеча входное сопротивление Ом. Поэтому для точной настройки в резонанс и обеспечения на заданной длине волны плечи СЭВ надо немного укоротить; величина укорочения зависит от радиуса плеча и определяется выражением [10, 11]

, (5.36)

требуемое для настройки в резонанс укорочение тем больше, чем толще вибратор, при этом лучше его диапазонные свойства;

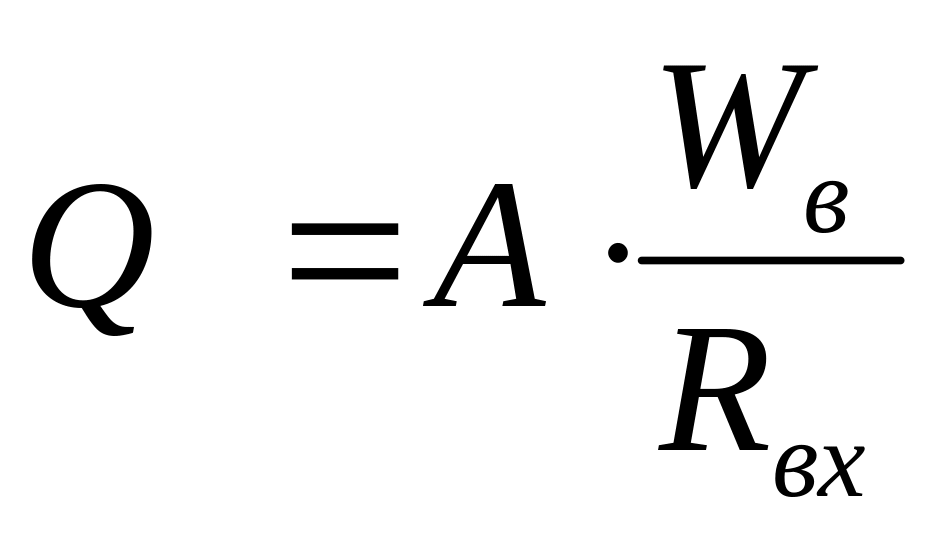3. частотная зависимость наиболее сильно выражена в случае тонких вибраторов и существенно ослабляется при увеличении толщины плеча. Это объясняется тем, что добротность СЭВ, прямо пропорциональная его волновому сопротивлению , соответственно снижается при увеличении радиуса плеча из-за уменьшения волнового сопротивления. В самом деле, добротность колебательной системы пропорциональна отношению запасенной в ней электромагнитной энергии к энергии, теряемой за период высокочастотных колебаний на резонансной частоте. В данном случае доля теряемой энергии входных колебаний вследствие излучения зависит только от отношения и почти не зависит от толщины СЭВ. Энергия, запасенная в ближней зоне вибратора, будет тем больше, чем тоньше его плечи. Поэтому при необходимости получения широкой полосы рабочих частот СЭВ (со слабой зависимостью от частоты) следует использовать толстые вибраторы — с плечами большого радиуса. Относительную полосу рабочих частот настроенного в резонанс полуволнового СЭВ можно рассчитать по приближенной формуле [10]

.

Примером широкополосного вибратора служит диапазонный вибратор Надененко (рис. 5.11), цилиндрические плечи которого имеют большой диаметр и выполняются обычно в виде набора проводников. Такие антенны широко применяются в качестве приемопередающих в стационарных системах радиосвязи ВЧ диапазона (на декаметровых волнах) [10].

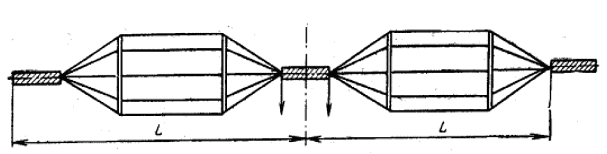
Рис. 5.11. Диапазонный вибратор Надененко

Надо также иметь в виду, что входное сопротивление СЭВ зависит и от конструкции его подключения к питающей линии передачи, как и в случае многих других антенн. По этой причине при проектировании антенн расчеты их входных сопротивлений носят, как правило, оценочный характер и уточняются путем компьютерного моделирования антенн с помощью специализированных программ и экспериментальных исследований характеристик опытных образцов антенн.