
- •Воронеж 2016
- •1. Основы теории антенн
- •1.1. Общие сведения об антеннах
- •1.2. Классификация антенн
- •1.3. Основные задачи теории антенн
- •1.4. Структура антенны. Электродинамические основы теории излучения антенн
- •1.5. Свойства электромагнитного поля антенн в дальней, промежуточной и ближней зонах
- •1.6. Расчет характеристик поля излучения в дальней зоне
- •1.7. Основные принципы технической электродинамики
- •1.8. Излучение элементарных источников
- •2. Основные электрические характеристики антенн
- •2.1. Характеристики направленности антенн в режиме излучения. Векторная комплексная характеристика направленности антенны
- •2.2. Коэффициент направленного действия и коэффициент усиления антенны
- •2.3. Входное сопротивление и полоса рабочих частот антенны
- •2.4. Характеристики антенн в режиме приема
- •2.5. Мощность, выделяющаяся в нагрузке приемной антенны
- •2.6. Согласование передающей и приемной антенн по поляризации
- •2.7. Шумовая температура приемной антенны
- •3. Излучение антенных решеток
- •3.1. Линейные антенные решетки с равноамплитудным возбуждением и линейным изменением фазы токов
- •3.2. Влияние неравномерности амплитудного распределения на направленность излучения линейных антенных решеток
- •3.3. Влияние фазовых искажений на дн линейной антенной решетки
- •3.4. Входное сопротивление излучающего элемента и мощность излучения антенной решетки
- •3.5. Кнд линейных антенных решеток
- •3.6. Понятие о непрерывном излучателе
- •3.7. Плоские антенные решетки
- •4. Излучение возбужденных поверхностей. Основы теории апертурных антенн
- •4.1. Направленные свойства прямоугольного и круглого раскрывов с синфазным и равноамплитудным возбуждением
- •4.2. Влияние неравномерного амплитудного распределения поля на диаграмму направленности излучающей поверхности
- •4.3. Кнд излучающей поверхности
- •5. Вибраторные антенны и решетки
- •5.1. Основы теории симметричного электрического вибратора
- •Решение уравнения (5.2) имеет вид [10, 11]
- •Приведем несколько распределений и по длине вибратора для различных , рассчитанных по формулам (5.4) и (5.6):
- •Не зависит от угла , то есть представляет собой окружность.
- •Диаграммы направленности сэв
- •Нормированная дн по напряженности поля
- •5.5. Симметричный щелевой вибратор
- •5.6. Излучение системы из двух вибраторов
- •5.7. Директорные антенны
- •5.8. Влияние идеально электропроводящей и бесконечно протяженной поверхности на излучение расположенных вблизи нее антенн
- •5.9. Несимметричный электрический вибратор
- •5.10. Коллинеарные антенны
- •5.11. Способы и устройства подключения вибраторных антенн к линиям передачи
- •6. Щелевые антенны и антенные решетки
- •Волноводно-щелевые антенные решетки
- •6.2. Перспективные щелевые антенные решетки свч и квч
- •7. Полосковые и микрополосковые антенны и антенные решетки
- •7.1. Принципы действия и основные характеристики резонаторных полосковых антенн
- •7.2. Линейные и плоские полосковые антенные решетки
- •8. Антенны вытекающей волны
- •8.1. Принципы построения антенн вытекающей волны
- •8.2. Плоские антенные решетки вытекающей волны
- •8.3. Плоские дифракционные антенны
- •9. Апертурные антенны
- •9.1. Волноводные излучатели
- •9.2. Рупорные антенны
- •9.3. Зеркальные антенны
- •Влияние отражений от зеркала на входное сопротивление антенны (реакция зеркала на облучатель)
- •Линзовые антенны
- •10. Широкополосные антенны
- •10.1. Логопериодические вибраторные антенны
- •10.2. Спиральные антенны
- •11.1. Фазированные антенные решетки
- •Характеристики фар
- •Соответственно, минимальное число излучателей [4, 14, 47]
- •Дискретность изменения фазы приводит к скачкообразному перемещению дн в пространстве и определяет точность установки дн.
- •11.2. Многолучевые антенные решетки
- •12. Методы экспериментальных исследований антенн. Автоматизированное проектирование антенно-фидерных устройств
- •12.1. Измерение диаграмм направленности антенн
- •12.2. Измерение коэффициента усиления антенны
- •12.3. Программные средства компьютерного моделирования и системы автоматизированного проектирования устройств свч и антенн
- •Антенно-фидерные устройства в авторской редакции
- •Подписано к изданию 05.02.2016. Объем данных 9000 Кб
- •3 94026 Воронеж, Московский просп., 14
5. Вибраторные антенны и решетки
5.1. Основы теории симметричного электрического вибратора
В теории антенн вибратором называют излучатель в виде тонкого электрического проводника (электрический вибратор) или узкой длиной щели, прорезанной в электропроводящем (металлическом) экране (магнитный, или щелевой вибратор) [2, 10, 11]. Вибраторы широко применяются как самостоятельные слабонаправленные антенны, так и в составе антенных решеток; в комбинации с рефлектором используются как однонаправленные антенны или облучатели зеркальных и линзовых антенн. Рабочие частоты вибраторных антенн и решеток обычно находятся в ВЧ-УВЧ диапазонах, хотя нередко вибраторы в полосковом или микрополосковом исполнении применяются и в СВЧ диапазоне.
В данном разделе под электрическим вибратором будем подразумевать излучатель ЭМВ в виде линейного цилиндрического проводника радиуса а с длиной плеч l1 и l2, к внутренним торцам которых, т.е. в зазоре шириной Δ, подключен источник ЭДС. Пусть ось z имеет начало в центре зазора и направлена вдоль оси вибратора. Вибратор может быть симметричным (СЭВ), если l1 = l2 = l, и несимметричным (НЭВ) в виде штыря высотой h, установленного, например, над электропроводящей плоскостью. Возбуждение СЭВ обычно осуществляется симметричной линией передачи (двухпроводной) или несимметричной (коаксиальной). В последнем случае необходимо симметрирующее устройство.
Рассмотрим СЭВ (рис. 5.1), находящийся в
свободном пространстве с волновым
сопротивлением
![]() Ом [2]. В случае малой ширины зазора Δ<<l
общая длина СЭВ L≈2l.
Ом [2]. В случае малой ширины зазора Δ<<l
общая длина СЭВ L≈2l.
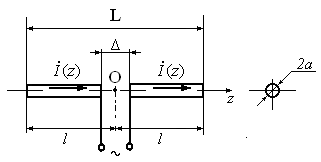
Рис. 5.1. Симметричный электрический вибратор
Под действием источника (генератора) ЭДС в плечах СЭВ возникают электрические токи, создающие в окружающем пространстве электромагнитное поле. В силу осевой симметрии СЭВ электрические токи на боковой поверхности его плеч имеют только продольные компоненты, а на торцах — радиальные. При анализе электрических характеристик СЭВ сначала решается внутренняя задача теории антенн — выясняется распределение тока на его поверхности; затем решается внешняя задача — определяется ЭМП излучения и другие характеристики.
В строгой постановке задача нахождения
распределения тока, наводимого в плечах
электрического вибратора с произвольными
длинами плеч под действием приложенного
к зазору высокочастотного напряжения
![]() ,
сводится к решению интегральных уравнений
[2, 5, 11].
,
сводится к решению интегральных уравнений
[2, 5, 11].
Для тонких электрических вибраторов
(![]() )
электродинамическая модель для нахождения
тока составляется на основе следующих
предположений [2, 5,1 1]:
)
электродинамическая модель для нахождения
тока составляется на основе следующих
предположений [2, 5,1 1]:
поверхностные продольные электрические токи
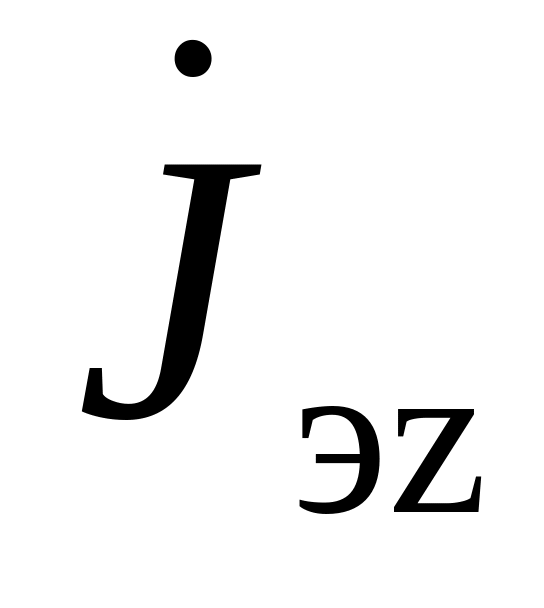 на
плечах вибратора вместе с эквивалентными
азимутальными магнитными токами
на
плечах вибратора вместе с эквивалентными
азимутальными магнитными токами
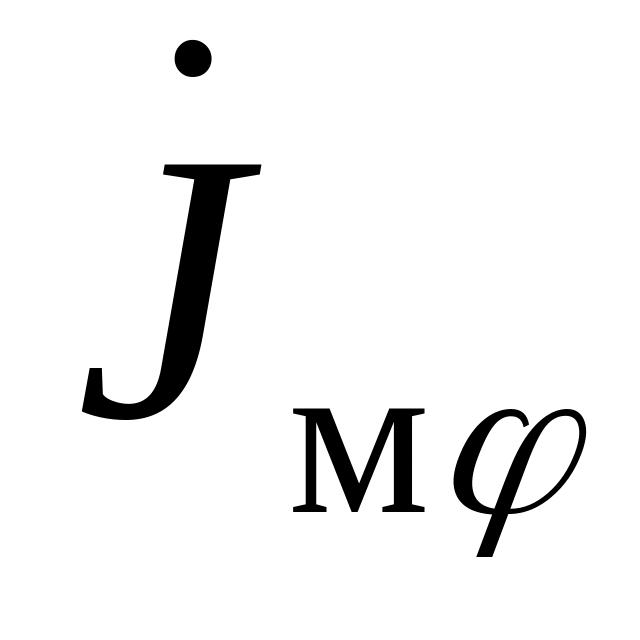 в
зазоре заменяются совпадающей с осью
вибратора бесконечно тонкой нитью
продольного электрического тока,
который считается непрерывным в зазоре
и равным нулю на торцах плеч, торцевые
токи не учитываются;
в
зазоре заменяются совпадающей с осью
вибратора бесконечно тонкой нитью
продольного электрического тока,
который считается непрерывным в зазоре
и равным нулю на торцах плеч, торцевые
токи не учитываются;тангенциальная компонента вектора
 ,
создаваемая нитью тока на воображаемой
боковой поверхности зазора, равна нулю
всюду кроме области зазора шириной Δ,
в которой эта компонента принимается
равной некоторой напряженности поля
возбуждения
,
создаваемая нитью тока на воображаемой
боковой поверхности зазора, равна нулю
всюду кроме области зазора шириной Δ,
в которой эта компонента принимается
равной некоторой напряженности поля
возбуждения
 .
.
В соответствии с (1.16) неизвестное на
данном этапе решения задачи распределение
тока
![]() создает
на воображаемой боковой поверхности
вибратора векторный электрический
потенциал, описываемый выражением [2,
5, 11]
создает
на воображаемой боковой поверхности
вибратора векторный электрический
потенциал, описываемый выражением [2,
5, 11]
![]() ,
(5.1)
,
(5.1)
где
![]() — ядро интеграла в виде функции разности
координат z точек
наблюдения и интегрирования zʹ,
поскольку
— ядро интеграла в виде функции разности
координат z точек
наблюдения и интегрирования zʹ,
поскольку
![]() .
Использование формулы перехода от
векторного потенциала к вектору
.
Использование формулы перехода от
векторного потенциала к вектору
![]() на боковой поверхности вибратора и
граничных условий для
на идеальной металлической поверхности
и на границе поверхность зазора —
окружающее пространство приводит к
интегро-дифференциальному уравнению
Поклингтона относительно
с
ядром
на боковой поверхности вибратора и
граничных условий для
на идеальной металлической поверхности
и на границе поверхность зазора —
окружающее пространство приводит к
интегро-дифференциальному уравнению
Поклингтона относительно
с
ядром
![]() .
После определенных преобразований оно
приводит к интегральному уравнению
Халлена—Леонтовича—Левина (далее —
Халлена) относительно искомого
распределения тока по вибратору [2, 5,
11]:
.
После определенных преобразований оно
приводит к интегральному уравнению
Халлена—Леонтовича—Левина (далее —
Халлена) относительно искомого
распределения тока по вибратору [2, 5,
11]:
![]() ,
(5.2)
,
(5.2)
где
![]() — напряжение, создаваемое генератором
на входе вибратора; А и В — произвольные
постоянные множители, определяемые из
условия равенства нулю тока на концах
вибратора;
— напряжение, создаваемое генератором
на входе вибратора; А и В — произвольные
постоянные множители, определяемые из
условия равенства нулю тока на концах
вибратора;
![]() — волновое сопротивление среды,
окружающей вибратор;
— волновое сопротивление среды,
окружающей вибратор;
![]() —
коэффициент фазы для плоской ЭМВ в
среде.
—
коэффициент фазы для плоской ЭМВ в
среде.
Это уравнение не имеет аналитического решения, и обычно его решают численно с введением ряда упрощений [2, 5, 11]. В результате получается приближенное выражение для тока, протекающего по плечам вибратора, которое для симметричного электрического вибратора имеет вид [2, 5, 10, 11]:
![]() ,
(5.3)
,
(5.3)
где
![]() — комплексная амплитуда тока в точках
питания СЭВ.
— комплексная амплитуда тока в точках
питания СЭВ.
В случае, когда СЭВ находится в свободном
пространстве, коэффициент фазы
![]() .
.
До разработки строгой теории симметричного вибратора при расчете тока в СЭВ и ЭМП излучения применялся приближенный метод. В его основу положено предположение о синусоидальном распределении тока по тонкому вибратору с плечами в виде идеальных электрических проводников, связанное с некоторой внешней аналогией между СЭВ и двухпроводной линией передачи, разомкнутой на конце. Переходя от двухпроводной линии к вибратору, полагают, что при этом закон распределения тока не нарушается, т.е.
![]() (5.4)
(5.4)
где
![]() — комплексная амплитуда тока в пучности;
—
комплексная амплитуда тока в точках
питания; l
— длина
плеча;
— комплексная амплитуда тока в пучности;
—
комплексная амплитуда тока в точках
питания; l
— длина
плеча;
![]() — расстояние от начала координат до
произвольной точки на поверхности
плеча;
— расстояние от начала координат до
произвольной точки на поверхности
плеча;
![]() — коэффициент фазы тока. При этом
считают, что фазовая скорость волны
тока равна скорости света в свободном
пространстве. Обратим внимание на то,
что выражения (5.3) и (5.4) совпадают.
— коэффициент фазы тока. При этом
считают, что фазовая скорость волны
тока равна скорости света в свободном
пространстве. Обратим внимание на то,
что выражения (5.3) и (5.4) совпадают.
Как видно из формулы
(5.1), при таком представлении распределение
тока не зависит от толщины вибратора.
В действительности, хотя и двухпроводная
линия и СЭВ являются колебательными
системами с распределенными параметрами,
они существенно различаются: распределенные
параметры L
и С
длинной линии постоянны по ее длине, а
у СЭВ они изменяются; линия практически
не излучает, СЭВ же создает излучение,
т.е. даже будучи выполненным из идеального
проводника, характеризуется потерями
энергии. Отметим, что в случае идеальной
разомкнутой двухпроводной линии ток
вдоль нее изменяется по закону стоячей
волны в соответствии с (5.1) и в узлах
равен нулю, а в случае СЭВ на самом деле
ток не может быть распределен по закону
(5.1) и в узлах не обращается в нуль [10,
11]. Однако расчет ЭМП излучения в дальней
зоне в предположении синусоидального
распределения тока по вибратору дает
хорошее совпадение с экспериментальными
данными для тонких вибраторов с
относительной длиной плеча
![]() .
.
При известном
законе распределения тока по вибратору
легко установить приближенный закон
распределения заряда, воспользовавшись
законом сохранения заряда. Считая, что
вибратор тонкий (a
<< l)
, можно
допустить, что ток
имеет
только продольную компоненту
![]() .
На основе уравнения непрерывности [6,
7] приближенное распределение электрического
заряда для линейного тока на плечах СЭВ
описывается уравнением
.
На основе уравнения непрерывности [6,
7] приближенное распределение электрического
заряда для линейного тока на плечах СЭВ
описывается уравнением
![]() ,
(5.5)
,
(5.5)
где
![]() —
заряд, приходящийся на единицу длины
вибратора, Кл/м.
—
заряд, приходящийся на единицу длины
вибратора, Кл/м.
